Laststufen für iterative Berechnung
Bei der nichtlinearen Berechnung eines "empfindlichen" Systems nahe am Stabilitätsversagen ist es oft schwierig, das Gleichgewicht zu finden. Deshalb besteht im Programm die Möglichkeit, die Belastung stufenweise aufzubringen: Sind beispielsweise zwei Laststufen vorgegeben, wird im ersten Schritt nur die halbe Last angesetzt. Es wird so lange iteriert, bis die Gleichgewichtsbedingungen erfüllt sind. Im zweiten Schritt wird dann die volle Belastung auf das bereits verformte System aufgebracht und wieder bis zur Konvergenz iteriert. Auf diese Weise lassen sich Berechnungsabbrüche infolge Instabilitäten vermeiden. Die Berechnung über Laststufen ist zwangsläufig mit einem erhöhten Zeitbedarf verbunden. Laststufen können sowohl global als auch spezifisch für Lastfälle und Lastkombinationen vorgesehen werden.
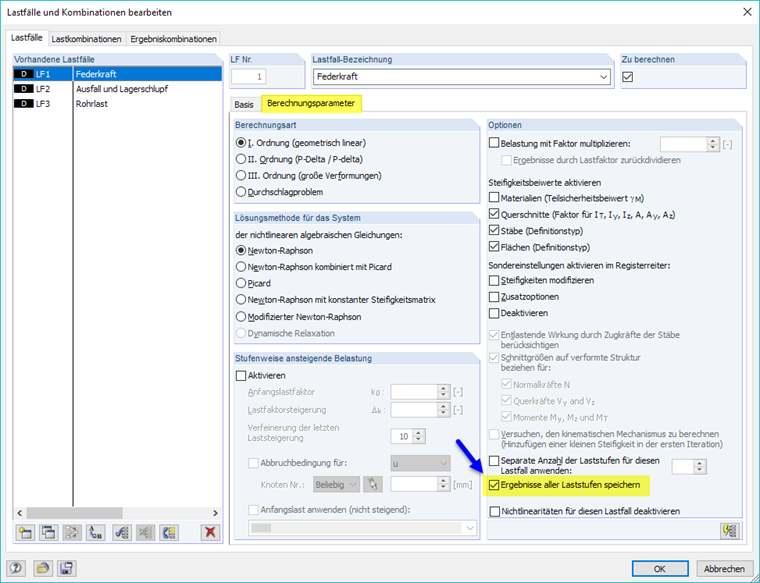
RFEM bietet auch die Möglichkeit an, die Ergebnisse der einzelnen Laststufen während der Berechnung zu speichern. Die entsprechende Einstellung ist im Register "Berechnungsparameter" des Lastfalls oder der Lastkombination vorzunehmen. Damit werden beispielsweise die Kräfte- und Momentenverläufe unter Berücksichtigung nichtlinearer Effekte transparent, die zu ausgeprägten Umlagerungen im Modell führen können.
Dieser Fachbeitrag stellt drei einfache Beispiele für iterative Berechnungen vor, die die schrittweise Entwicklung der Ergebnisse unter steigenden Lastniveaus veranschaulichen.
Feder mit Anschlag
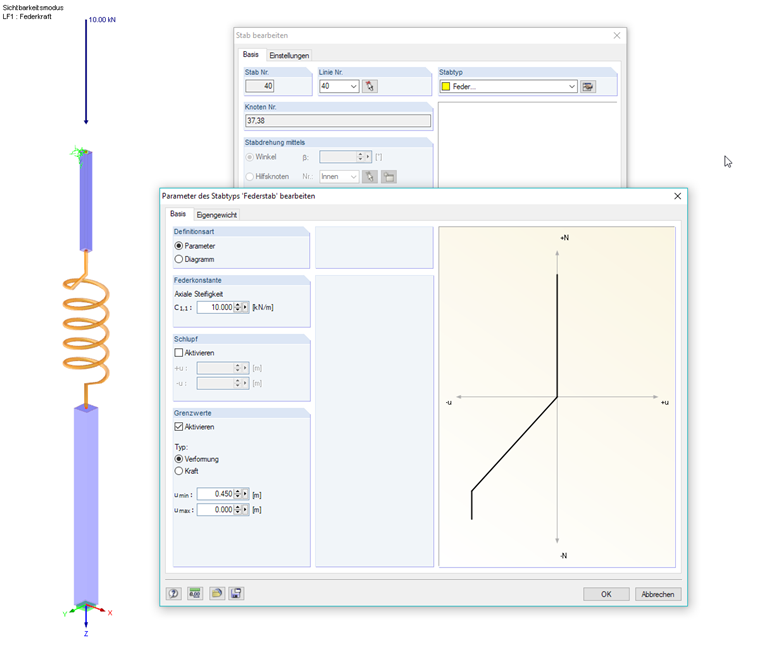
Ein druckbelasteter Teleskopstab wird durch zwei Rohre abgebildet, deren Verschiebung über eine zwischengeschaltete Feder gesteuert wird. Die axiale Steifigkeit der Feder und die Begrenzung der Verformung oder Kraft kann im Dialog "Parameter des Stabtyps 'Feder' bearbeiten" festgelegt werden. Im Beispielmodell wird keine Druckkraft mehr kompensiert, wenn eine Stauchung von 45 cm erreicht ist.
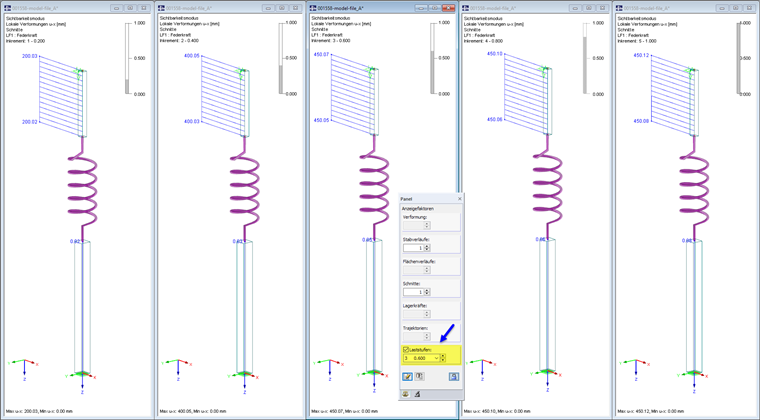
Die Knotenlast wird in fünf Laststufen aufgebracht. Die Berechnung erfolgt nach Theorie I. Ordnung. Bei 20 % und 40 % der Last liegt die Verformung der Feder mit 20 cm und 40 cm im wirksamen Arbeitsbereich. Der obere Stab verschiebt sich entsprechend nach unten. Wird die Last auf 60 %, 80 % und schließlich 100 % gesteigert, stellt sich ab dem Federweg von 45 cm kein weiterer Verformungszuwachs ein. Die Verformung des oberen Stabes bleibt konstant. Die minimalen Differenzen bei den Nachkommastellen beruhen auf den Stauchungen der Rohrstäbe.
Rahmen mit normalkraftbegrenzten Diagonalen und Lager mit Schlupf
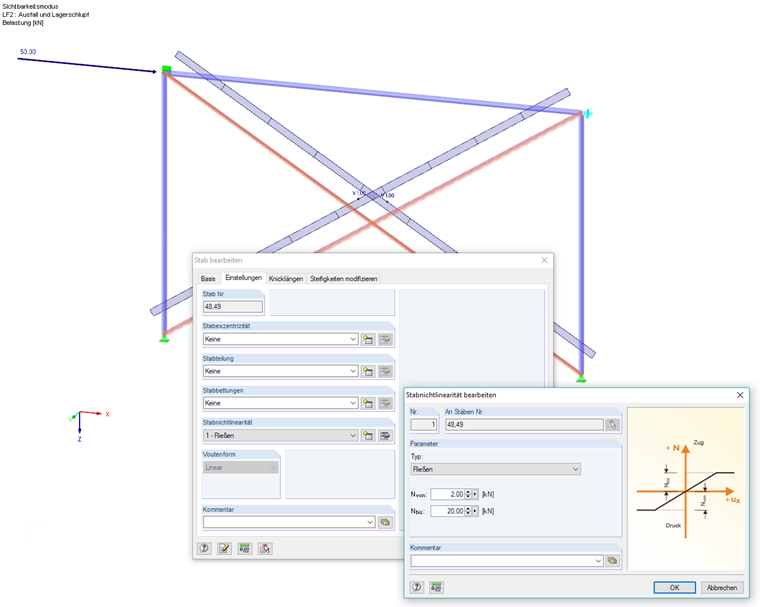
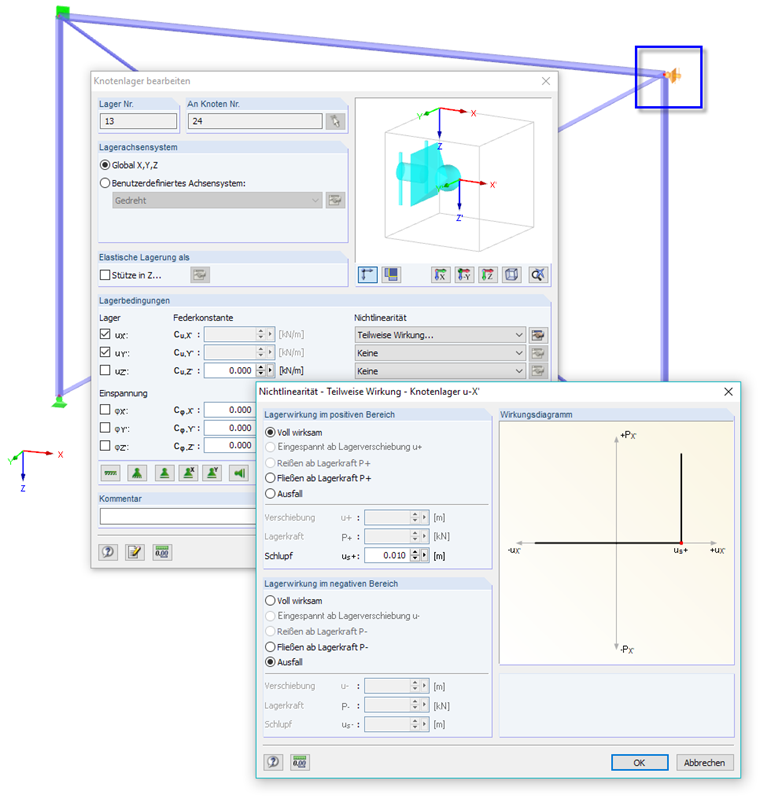
Ein Rahmen ist durch einen Diagonalverband ausgesteift. Die Normalkrafttragfähigkeit der vorgespannten L-Profile wird durch ein Fließkriterium geregelt: Es sind nur Druckkräfte bis 2 kN und Zugkräfte bis 20 kN aufnehmbar. Kräfte außerhalb dieses Bereichs vergrößern die Dehnung ohne weitere Kräfteaufnahme.
Zusätzlich ist ein nichtlinear wirkendes Horizontallager mit Schlupf an einer Rahmenecke vorgesehen, das eine angrenzende Wand abbildet. Es wirkt nur für Druckkräfte, sobald sich eine horizontale Knotenverschiebung von 1 cm einstellt.
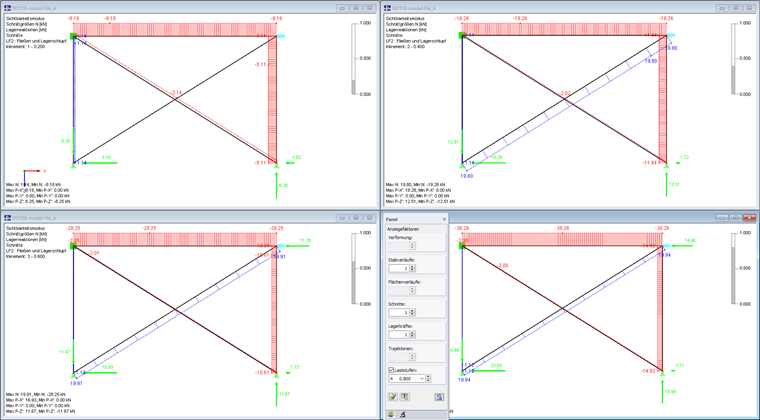
Die Knotenlast wird wieder in fünf Laststufen aufgebracht. Die Berechnung erfolgt nach Theorie II. Ordnung. Bei einem Lastniveau von 20 % ist eine Diagonale ausreichend, um die Knotenlast über eine Druckkraft im System zu verlagern. Bei 40 % der Last stellt sich zusätzlich in der zweiten Diagonale eine Zugkraft ein. Beide Diagonalen zeigen bereits ein Fließverhalten. Sie sind aber ausreichend, um das System ohne das Horizontallager zu stabilisieren. Dieses Lager ist erst ab 60 % der Last wirksam.
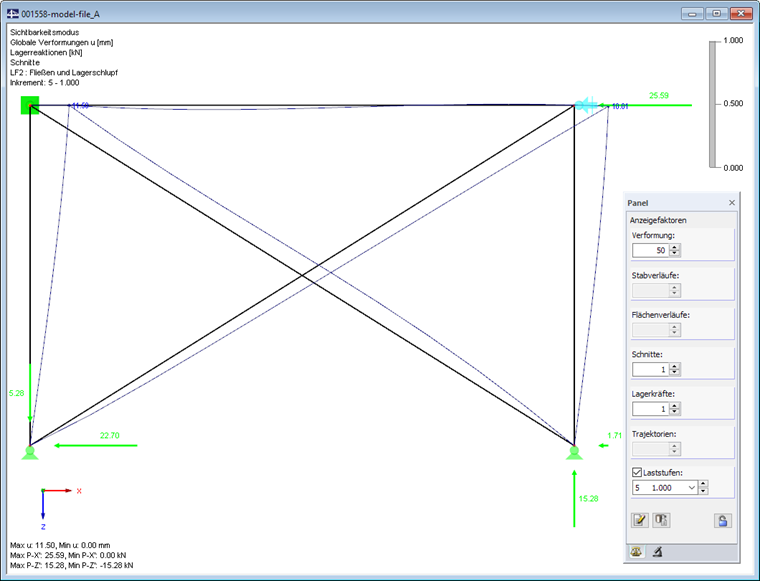
In den weiteren Laststufen sind die Umlagerungseffekte abgeschlossen. Am nunmehr gelagerten Knoten in der Rahmenecke stellt sich (unter Berücksichtigung des Z-Anteils) eine Gesamtverformung von 10.01 mm ein.
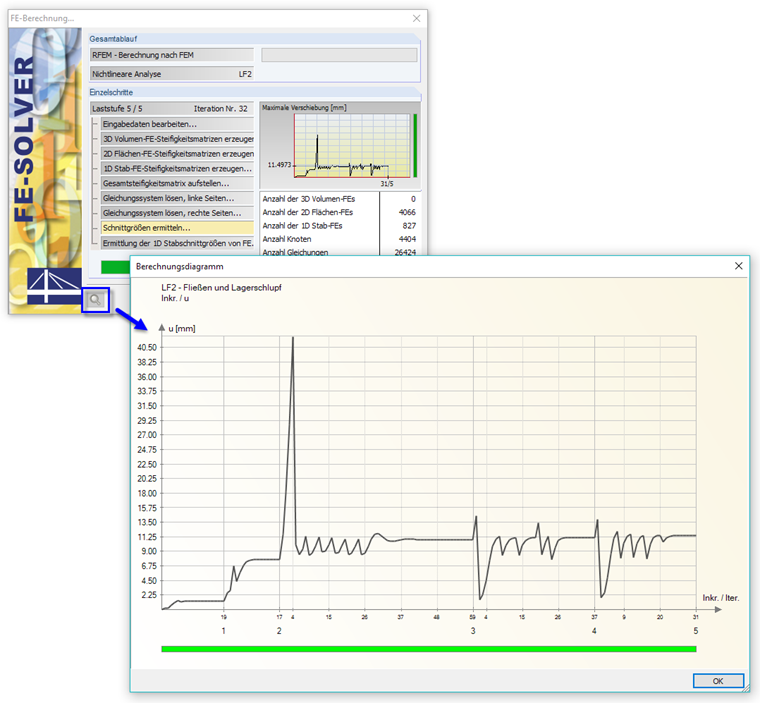
Während der Berechnung wird der Verlauf der Verformungen (Standard) in den einzelnen Laststufen als Diagramm dargestellt. Sind die Verformungen im verträglichen Bereich, ist der Balken grün. Ein roter Balken bedeutet in den meisten Fällen, dass zu große Verdrehungen (0.1 rad oder mehr) vorliegen. Die Berechnungsdiagramme sind auch nach der Berechnung im Dialog "Berechnungsparameter", Register "Berechnungsdiagramme" für eine detaillierte Auswertung zugänglich.
Rahmenecke mit plastischem Materialverhalten
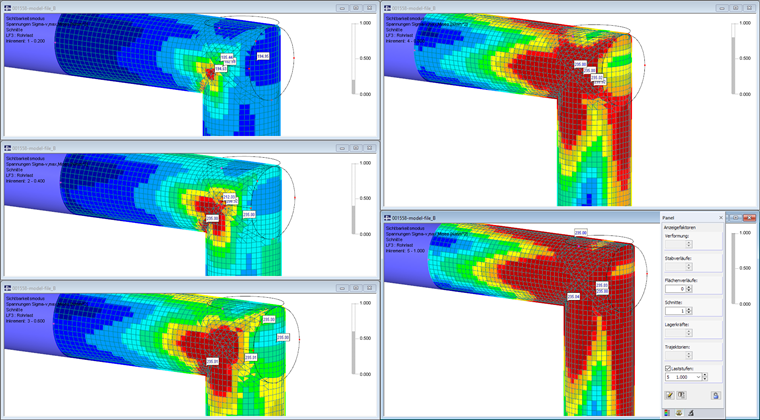
Ein Rahmen aus Stahlrohr ist durch eine Vertikallast beansprucht. Für die plastische Untersuchung einer Rahmenecke wird dieser Bereich über Flächendurchdringungen modelliert. Die Flächen weisen ein isotrop plastisches Materialverhalten auf: Ab dem Erreichen der Fließspannung von 235 N/mm² ist kein weiterer Spannungszuwachs möglich.
Für die Analyse des nichtlinearen Materialverhaltens ist das Zusatzmodul RF-MAT NL erforderlich. Es werden wieder fünf Laststufen angesetzt. Die Ergebnisse der Vergleichsspannungen zeigen den Fortschritt des Plastizierens auf den einzelnen Lastniveaus. Für die Auswertung einer plastischen Analyse sollte der Verlauf der Spannungen "Konstant in Elementen" gewählt werden (siehe auch Knowledge Base: Glättungsvarianten).
Zusammenfassung
In diesem Beitrag wurden einige einfache Beispiele für die Berechnung mit Laststufen vorgestellt. Diese Herangehensweise eignet sich grundsätzlich bei sensiblen Systemen oder zur Berücksichtigung großer Verformungen, aber auch bei gezielten Untersuchungen des Tragwerksverhaltens im Hinblick auf Umlagerungen oder nichtlineare Effekte.
Bei nichtlinearen Berechnungen ist grundsätzlich für eine ausreichend hohe Anzahl möglicher Iterationen zu sorgen. Sollte sich keine Konvergenz innerhalb dieses Limits einstellen, erscheint am Ende der Berechnung eine entsprechende Meldung. Die Ergebnisse der unvollendeten Analyse können anschließend eingesehen werden, um Problembereiche zu lokalisieren oder die Berechnungsparameter anzupassen.
Die Ergebnisgrafiken der einzelnen Laststufen lassen sich nicht zuletzt im Ausdruckprotokoll dokumentieren und so für die Nachvollziehbarkeit der statischen Untersuchung nutzen.