Os cantos de paredes são frequentemente singularidades e têm de ser considerados do ponto de vista da engenharia. Singularitäten werden meist durch einspringende Ecken und durch große Steifigkeitssprünge hervorgerufen.
Da es sich somit nicht um ein Problem im Programm handelt, kann ich Ihnen nur eine mögliche Vorgehensweise zur Ermittlung der Bemessungsquerkraft am Beispiel erläutern. Als Grundlage fürs Beispiel verwende ich die Literatur "Beispiele zur Bemessung nach DIN 1045-1; Band 1: Hochbau (3. Auflage)" vom Verlag Ernst & Sohn. (Auszug finden Sie im Anhang)
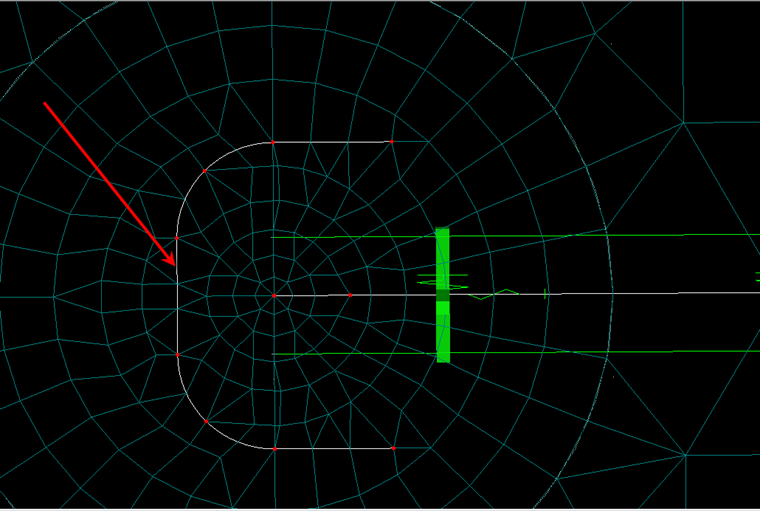
Ziel ist es sich die Bemessungsquerkraft am kritischen Rundschnitt zu ermitteln. Ermitteln Sie sich die Abmessungen des kritischen Rundschnittes nach DIN 1045-1, Bild 38 bzw. Bild 39 und erzeugen Sie diese Linien in RFEM (siehe Bild 1).
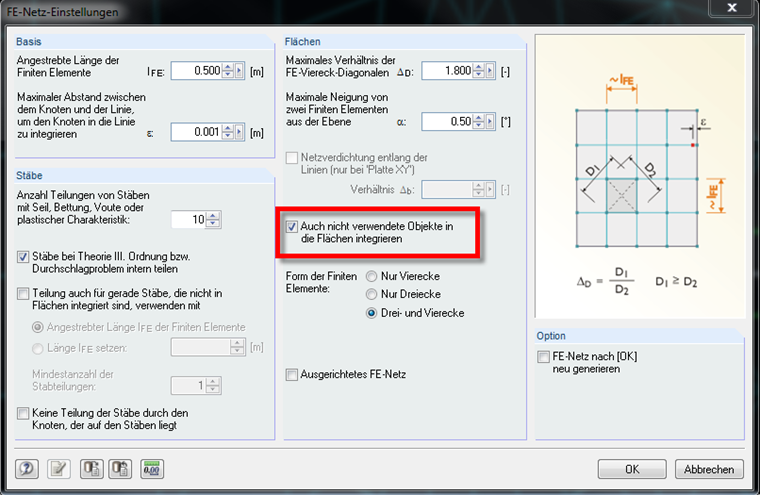
Damit die erzeugten Linien in die Fläche mit einbezogen wird klicken Sie bitte auf Berechnung → FE-Netz-Einstellungen und wählen dann folgende Option (siehe Bild 2). Führen Sie gegebenenfalls eine Netzverdichtung durch.
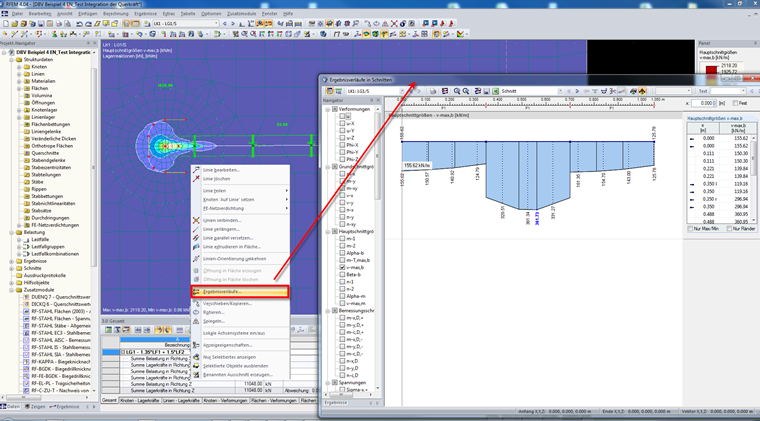
Nach Berechnung der maßgebenden Lastfallkombination selektieren Sie bitte erst die drei geraden Linien und klicken dann mit der rechten Maustaste auf eine davon. Wählen Sie dann Ergebnisverläufe (siehe Bild 3).
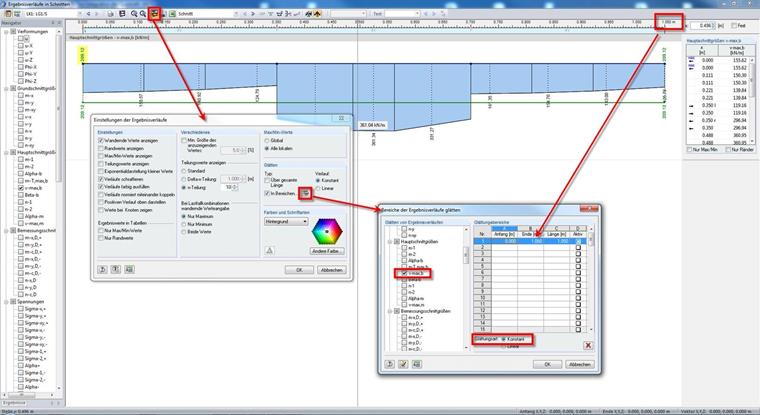
Lassen Sie sich nun die Ergebnisse von vmax,b mit folgenden Einstellungen glätten (siehe Bild 4).
Notieren Sie sich den geglätteten Wert (im Bild 209,12 kN/m) sowie die die Gesamtlänge (im Bild 1,05 m). Glätten Sie nun die Bogenlinien analog zu den geraden Linien. (Es lassen sich nämlich nur Linien desselben Typs gleichzeitig auswählen um daran die Ergebnisverläufe anzeigen zu lassen.) Notieren Sie auch hier den geglätteten vmax,b (221,04 kN/m) und die Länge (0,889m). Mit diesen Werten können Sie sich nun die Bemessungsquerkraft für den Durchstanznachweis ermitteln:
vEd = β x (209,12 kN/m x 1,05 m + 221,04 x 0,889 m) / (1,05 m + 0,889 m) = 289,69 kN/m
mit β = 1,35 für Wandenden und
β = 1,2 für Wandecken (nach DIN 1045-1; Bild 44)
VEd = 289,69 kN/m / β x (1,05 m + 0,889 m) = 416,08 kN