401x

2020-06-27

Flessione plastica di una piastra sottile sotto carico continuo

Descrizione

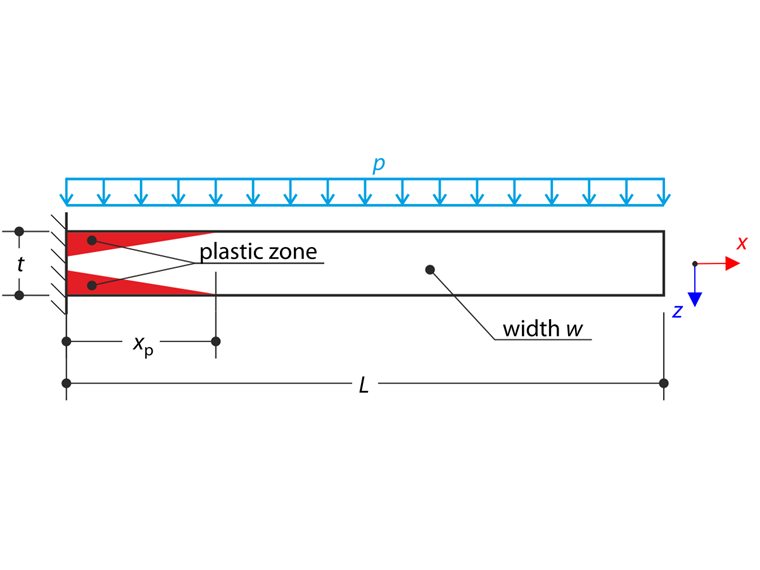
Una piastra sottile è completamente fissata all'estremità sinistra e sottoposta a una pressione uniforme. In questo esempio, vengono considerate piccole deformazioni e il peso proprio è trascurato. Il problema è descritto dal seguente set di parametri. Determina la freccia massima u_z,max.

Materiale	Elastico-plastico	Modulo di elasticità	E	210000.000	MPa
		coefficiente di Poisson	ν	0.000	-
		Modulo di taglio	G	105000.000	MPa
		Tensione di snervamento	f_y	40,000	MPa
Geometria	Piastra	Durata	L	1.000	m
		Larghezza	w	0.050	m
		spessore	t	0.005	m
Carico		Pressione uniforme	p	2,750	kPa

Flessione plastica - Carico continuo

Soluzione analitica

Le quantità del carico sono discusse all'inizio. Il momento M_e quando si verifica il primo snervamento e il momento ultimo M_p quando la struttura diventa cerniera plastica sono calcolati come segue:

M_{e} = 2 \int_{0}^{t / 2} σ (z) zw dz = 2 \int_{0}^{t / 2} \frac{2 f_{y}}{t} z^{2} w dz = \frac{f_{y} {wt}^{2}}{6}

Momento elastico

M_{p} = 2 \int_{0}^{t / 2} σ (z) zw dz = 2 \int_{0}^{t / 2} f_{y} zw dz = \frac{f_{y} {wt}^{2}}{4}

Momento plastico ultimo

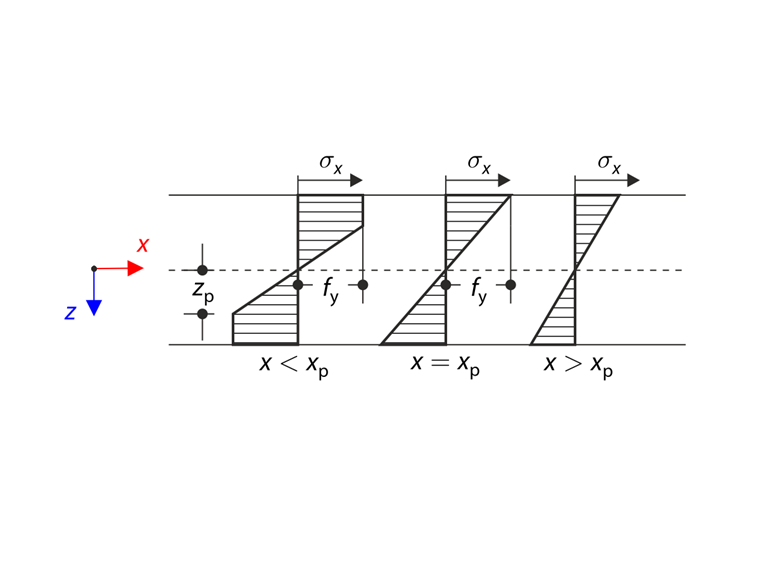
La piastra è portata nello stato elastico-plastico dalla pressione p. La tensione di flessione è definita secondo la seguente formula:

σ_{x} (x, z) = - κ (x) Ez

Tensione di flessione

dove κ è la curvatura. La lunghezza della zona elastico-plastica è descritta dal parametro x_p. La quantità di tensione di flessione sulla superficie è uguale alla resistenza plastica f_y nel punto x_p, vedere lo schema seguente.

Distribuzione della tensione di flessione

Il momento elastico-plastico M_ep (forza interna) deve essere uguale al momento flettente M (forza esterna). La curvatura κ_p nella zona elastico-plastica risulta da questa uguaglianza.

κ_{p} = \frac{1}{E} \sqrt{\frac{\frac{f_{y}^{3} w}{3}}{- \frac{q (L - x)^{2}}{2} + \frac{f_{y} t^{2} w}{4}}}

Curvatura nella zona elastico-plastica

u_{z, \max} = \int_{0}^{x_{p}} κ_{p} (L - x) dx + \int_{x_{p}}^{L} κ_{e} (L - x) dx = 83.117 + 83.117 = 166.234 mm

Inflessione massima dello sbalzo

Impostazioni di RFEM

Modellato in RFEM 5.26 e RFEM 6.01
La dimensione dell'elemento è l_FE =0,020 m
Nel caso di modelli solidi, viene utilizzato l'infittimento della mesh attraverso lo spessore (6 elementi per spessore)
Viene considerata l'analisi geometricamente lineare
Il numero di incrementi è 5
La rigidezza a taglio delle aste è trascurata

Risultati

Modello	Soluzione analitica	RFEM 5		RFEM 6
Modello	u_z,max [mm]	u_z,max [mm]	Rapporto [-]	u_z,max [mm]	Rapporto [-]
Plastico isotropo 1D	166,234	166.214	1.000	166.018	0,999
Isotropo plastico 2D/3D, piastra		162.987	0,980	162.960	0,980
Isotropo elastico non lineare 2D/3D, piastra, von Mises		165.730	0,997	165.700	0,997
Isotropo elastico non lineare 2D/3D, piastra, Tresca		166.998	1.005	166.969	1.004
Isotropo plastico 2D/3D, solido		160.601	0,966	162.429	0,977
Isotropo elastico non lineare 2D/3D, solido, von Mises		163.003	0,981	165.593	0,996
Isotropo elastico non lineare 2D/3D, solido, Tresca		168.725	1.015	169.691	1.021
Isotropo elastico non-lineare 1D		166.214	1.000	166.018	0,999

Nota: La deviazione dei risultati è causata anche dalla differenza tra la costante di torsione analitica e calcolata numericamente.

489x

12x

Esempio di verifica 0017 | 1

Bibliografia

Lublino, J. (1990). Teoria della plasticità. New York: Macmillan.

;