199x

2020-06-27

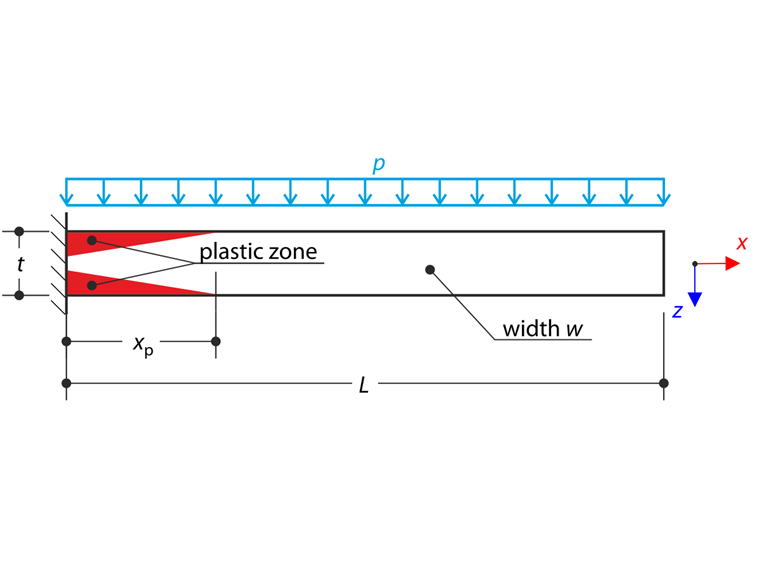
VE 0017 | Plastic Bending – Continuous Load

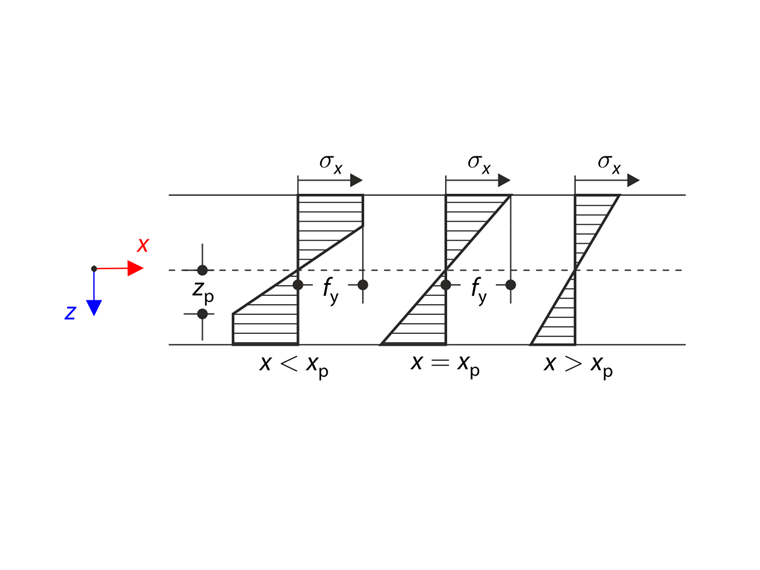
Description

A thin plate is fully fixed on the left end and subjected to a uniform pressure. Small deformations are considered and the self-weight is neglected in this example. The problem is described by the following set of parameters. Determine the maximum deflection u_z,max.

Material	Elastic-Plastic	Modulus of Elasticity	E	210000.000	MPa
		Poisson's Ratio	ν	0.000	-
		Shear Modulus	G	105000.000	MPa
		Yield Strength	f_y	40.000	MPa
Geometry	Plate	Length	L	1.000	m
		Width	w	0.050	m
		Thickness	t	0.005	m
Load		Uniform Pressure	p	2.750	kPa

Plastic Bending – Continuous Load

Analytical Solution

The quantities of the load are discussed at first. The moment M_e when the first yield is occurred and the ultimate moment M_p when the structure becomes plastic hinge are calculated as follows:

M_{e} = 2 \int_{0}^{t / 2} σ (z) zw dz = 2 \int_{0}^{t / 2} \frac{2 f_{y}}{t} z^{2} w dz = \frac{f_{y} {wt}^{2}}{6}

Elastic Moment

M_{p} = 2 \int_{0}^{t / 2} σ (z) zw dz = 2 \int_{0}^{t / 2} f_{y} zw dz = \frac{f_{y} {wt}^{2}}{4}

Ultimate Plastic Moment

The plate is brought into the elastic-plastic state by the pressure p. The bending stress is defined according to the following formula:

σ_{x} (x, z) = - κ (x) Ez

Bending Stress

where κ is the curvature. The elastic-plastic zone length is described by the parameter x_p. The bending stress quantity on the surface is equal to the plastic strength f_y at the point x_p, see the following schema.

Bending Stress Distribution

The elastic-plastic moment M_ep (internal force) has to equal to the bending moment M (external force). The curvature κ_p in the elastic-plastic zone results from this equality.

κ_{p} = \frac{1}{E} \sqrt{\frac{\frac{f_{y}^{3} w}{3}}{- \frac{q (L - x)^{2}}{2} + \frac{f_{y} t^{2} w}{4}}}

Curvature in Elastic-Plastic Zone

u_{z, \max} = \int_{0}^{x_{p}} κ_{p} (L - x) dx + \int_{x_{p}}^{L} κ_{e} (L - x) dx = 83.117 + 83.117 = 166.234 mm

Maximum Deflection of Cantilever

RFEM Settings

Modeled in RFEM 5.26 and RFEM 6.01
The element size is l_FE=0.020 m
In case of solid models mesh refinement across the thickness is used (6 elements per thickness)
Geometrically linear analysis is considered
The number of increments is 5
Shear stiffness of the members is neglected

Results

Model	Analytical Solution	RFEM 5		RFEM 6
Model	u_z,max [mm]	u_z,max [mm]	Ratio [-]	u_z,max [mm]	Ratio [-]
Isotropic Plastic 1D	166.234	166.214	1.000	166.018	0.999
Isotropic Plastic 2D/3D, Plate		162.987	0.980	162.960	0.980
Isotropic Nonlinear Elastic 2D/3D, Plate, von Mises		165.730	0.997	165.700	0.997
Isotropic Nonlinear Elastic 2D/3D, Plate, Tresca		166.998	1.005	166.969	1.004
Isotropic Plastic 2D/3D, Solid		160.601	0.966	162.429	0.977
Isotropic Nonlinear Elastic 2D/3D, Solid, von Mises		163.003	0.981	165.593	0.996
Isotropic Nonlinear Elastic 2D/3D, Solid, Tresca		168.725	1.015	169.691	1.021
Isotropic Nonlinear Elastic 1D		166.214	1.000	166.018	0.999

424x

Verification Example 0017 | 1

References

Lubliner, J. (1990). Plasticity Theory. New York: Macmillan.

;