Beschreibung
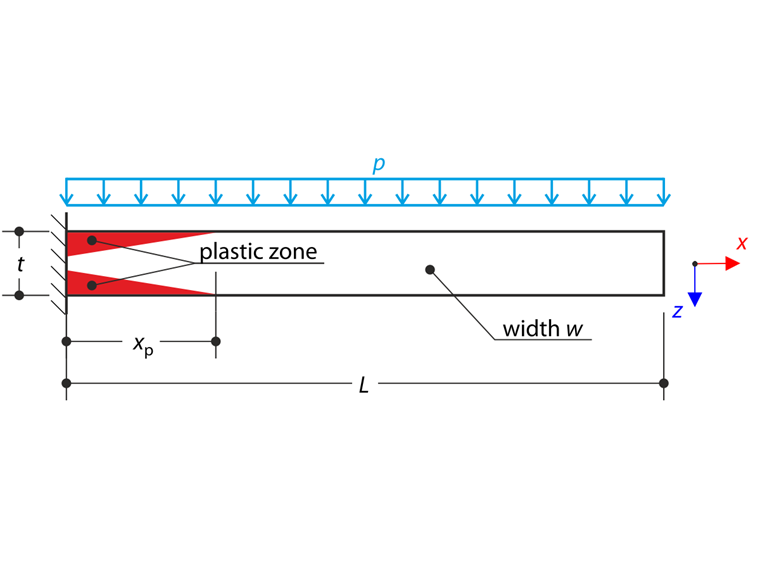
Eine dünne Platte ist am linken Ende vollständig befestigt und einem konstanten Druck ausgesetzt. In diesem Beispiel werden kleine Verformungen berücksichtigt und das Eigengewicht wird vernachlässigt. Das Problem wird durch folgenden Parametersatz beschrieben. Es soll die maximale Durchbiegung uz,max bestimmt werden.
| Material | Elastisch-Plastisch | Elastizitätsmodul | E | 210000,000 | MPa |
| Querdehnzahl | ν | 0,000 | - | ||
| Schubmodul | G | 105000,000 | MPa | ||
| Fließgrenze | fy | 40,000 | MPa | ||
| Geometrie | Platte | Länge | L | 1,000 | m |
| Breite | w | 0,050 | m | ||
| Stärke | t | 0,005 | m | ||
| Last | Gleichmäßiger Druck | S | 2,750 | kPa | |
Analytische Lösung
Zunächst werden die Größen der Last erläutert. Das Moment Me beim Auftreten der ersten Plastifizierung und das Bruchmoment Mp beim Übergang zum plastischen Gelenk werden wie folgt berechnet:
Die Platte wird durch den Druck p in den elastisch-plastischen Zustand gebracht. Die Biegespannung wird nach folgender Formel definiert:
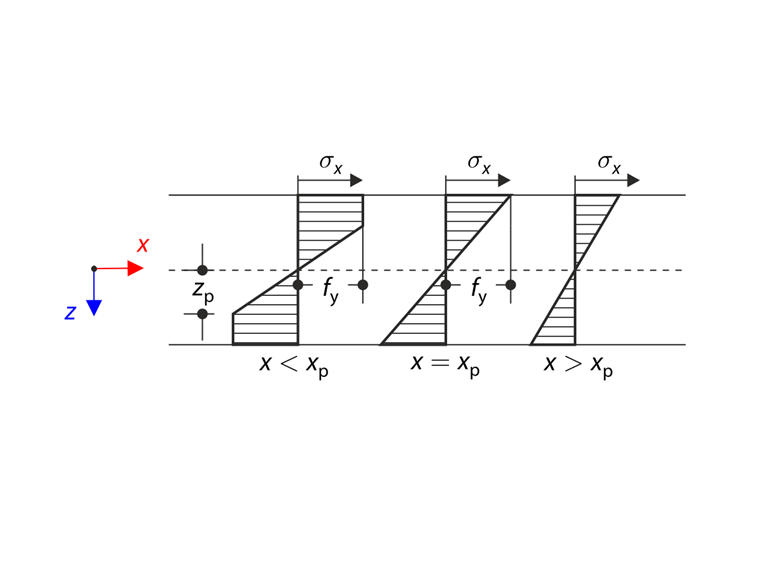
κ = Krümmung Die elastisch-plastische Zonenlänge wird durch den Parameter xp beschrieben. Die Biegespannungsgröße an der Oberfläche ist gleich der plastischen Festigkeit fy am Punkt xp, siehe folgendes Schema.
Das elastisch-plastische Moment Mep (Schnittgröße) muss gleich dem Biegemoment M (äußere Kraft) sein. Aus dieser Gleichheit ergibt sich die Krümmung κp im elastisch-plastischen Bereich.
RFEM-Einstellungen
- Modelliert in RFEM 5.26 und RFEM 6.01
- Die Elementgröße beträgt lFE =0,020 m
- Bei Volumenmodellen wird eine Netzverdichtung über die Dicke verwendet (6 Elemente pro Dicke)
- Theorie I. Ordnung wird berücksichtigt.
- Die Anzahl der Inkremente beträgt 5.
- Die Schubsteifigkeit der Stäbe wird vernachlässigt.
Ergebnisse
| Modell | Analytische Lösung | RFEM 5 | RFEM 6 | ||
| uz,max [mm] | uz,max [mm] | Ausnutzung [-] | uz,max [mm] | Ausnutzung [-] | |
| Isotrop plastisch 1D | 166,234 | 166,214 | 1,000 | 166,018 | 0,999 |
| Isotrop plastisch 2D/3D, Platte | 162,987 | 0,980 | 145,860 | 0,980 | |
| Isotrop nichtlinear elastisch 2D/3D, Platte, von Mises | 155,730 | 0,997 | 165,700 | 0,997 | |
| Isotrop nichtlinear elastisch 2D/3D, Platte, Tresca | 166,998 | 1,005 | 166,969 | 1,004 | |
| Isotrop plastisch 2D/3D, Volumenkörper | 160,601 | 0,966 | 162,429 | 0,977 | |
| Isotrop nichtlinear elastisch 2D/3D, Volumenkörper, von Mises | 163,003 | 0,981 | 165,593 | 0,996 | |
| Isotrop nichtlinear elastisch 2D/3D, Volumenkörper, Tresca | 168,725 | 1,015 | 169,691 | 1,021 | |
| Isotrop nichtlinear elastisch 1D | 166,214 | 1,000 | 166,018 | 0,999 | |
Anmerkung: Die Abweichung der Ergebnisse wird ebenfalls durch den Unterschied zwischen analytischem und numerisch berechnetem Torsionsträgheitsmoment verursacht.
_1.jpg?mw=350&hash=ab2086621f4e50c8c8fb8f3c211a22bc246e0552)