Zpět na příklady
Je tato stránka užitečná?
241x
009017
27.6.2020

Plastický ohyb tenké desky při spojitém zatížení

Popis

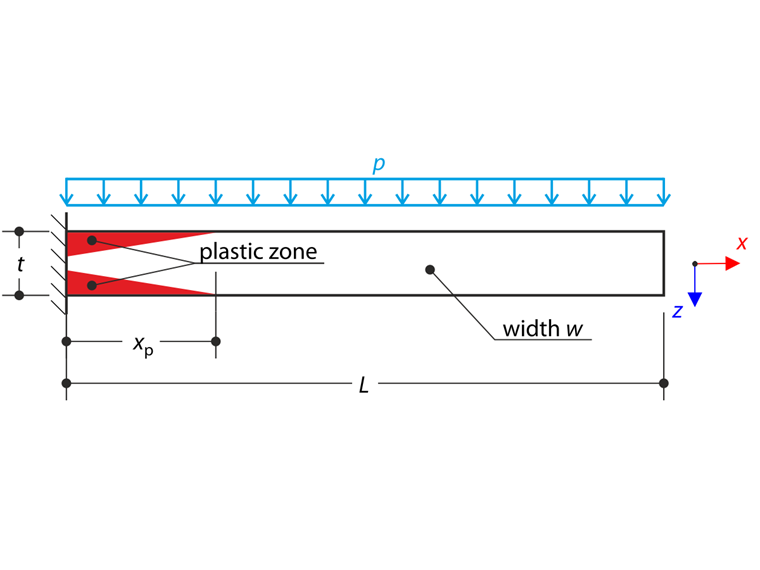
Tenká deska je zcela upevněna na levém konci a vystavena konstantnímu tlaku. V tomto příkladu se zohlední malé deformace a vlastní tíha se zanedbá. Problém je popsán pomocí následující sady parametrů. Stanovíme maximální průhyb uz,max.

Materiál Pružný-plastický Modul pružnosti E 210000,000 MPa
Poissonův součinitel ν 0,000 -
Smykový modul G 105000,000 MPa
Mez kluzu fy 40,000 MPa
Geometrie Deska obvod L 1,000 m
Šířka w 0,050 m
Tloušťka t 0,005 m
Zatížení Konstantní tlak p 2,750 kPa
Plastický ohyb - spojité zatížení
Plastický ohyb - spojité zatížení

Analytické řešení

Nejdříve se budeme zabývat velikostmi zatížení. MomentMe při prvním tečení a mezní momentMp, kdy se konstrukce stává plastickým kloubem, se počítají následovně:

Me=2∫0t/2σ(z)zw dz=2∫0t/22fytz2w dz=fywt26
Pružný moment
Mp=2∫0t/2σ(z)zw dz=2∫0t/2fyzw dz=fywt24
Mezní plastický moment

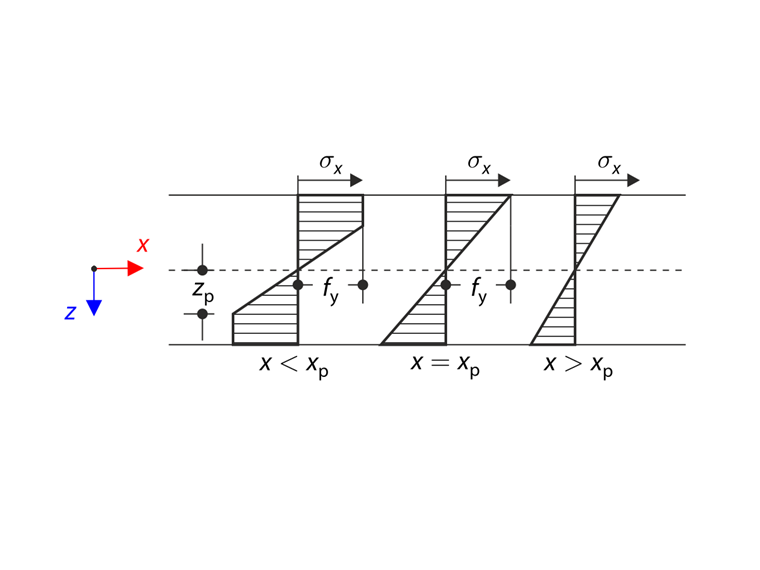
Tlakem p se deska uvede do pružno-plastického stavu. Napětí v ohybu se definuje podle následujícího vzorce:

σx(x,z)=-κ(x)Ez
ohybové napětí

kde κ je zakřivení. Délka pružno-plastické oblasti je definována parametrem xp. Velikost ohybového napětí na ploše se rovná plastické pevnosti fy v bodě xp, viz následující schéma.

Průběh napětí v ohybu
Průběh napětí v ohybu

Pružno-plastický momentMep (vnitřní síla) se musí rovnat ohybovému momentu M (vnější síla). Z této rovnosti vyplývá zakřiveníκp v pružně-plastické oblasti.

κp=1Efy3w3-q(L-x)22+fyt2w4
Zakřivení v elasticko-plastické oblasti
uz,max=∫0xpκp(L-x)dx+∫xpLκe(L-x)dx=83.117+83.117=166.234 mm
Maximální průhyb konzoly

Nastavení programu RFEM

  • Modelováno v programech RFEM 5.26 a RFEM 6.01
  • Velikost prvku je lFE = 0,020 m
  • V případě modelů těles se používá zahuštění sítě po celé tloušťce (6 prvků na tloušťku)
  • Uvažuje se geometricky lineární analýza
  • Počet přírůstků je 5
  • Smyková tuhost prutů se zanedbává

Výsledky

Model Analytické řešení RFEM 5 RFEM 6
uz,max [mm] uz,max [mm] Poměr [-] uz,max [mm] Poměr [-]
Izotropní plastický 1D 166,234 166,214 1,000 166,018 0,999
Izotropní plastický 2D/3D, deska 162,987 0,980 162,960 0,980
Izotropní nelineární elastický 2D/3D, deska, von Mises 165,730 0,997 165,700 0,997
Izotropní nelineární elastický 2D/3D, deska, Tresca 166,998 1,005 166,969 1,004
Izotropní plastický 2D/3D, těleso 160,601 0,966 162,429 0,977
Izotropní nelineární elastický 2D/3D, těleso, von Mises 163,003 0,981 165,593 0,996
Izotropní nelineární elastický 2D/3D, těleso, Tresca 168,725 1,015 169,691 1,021
Izotropní nelineárně elastický 1D 166,214 1,000 166,018 0,999

Poznámka: Odchylka výsledků je také způsobena rozdílem mezi analytickou a numericky vypočítanou konstantou kroucení.

Verifikační příklad 0017 | 1
429x
6x
Verifikační příklad 0017 | 1
Reference
  1. Lubliner, J. (1990). Teorie plasticity. New York: Macmillan.
  • Mia: AI asistentka
  • Nejnovější verifikační příklady
Události
Videa
Modely ke stažení
Články z databáze znalostí
KB 001879 | Vliv ohybové tuhosti lan
V tomto příspěvku ukážeme a vysvětlíme vliv ohybové tuhosti lan na jejich vnitřní síly. Poradíme také, jak tento vliv snížit.
Export options for RFEM 6 to DXF file are displayed in a clear interface layout.
V tomto článku uvádíme podrobný přehled funkcí pro export z programů RFEM 6 a RSTAB 9 do souborů AutoCAD/DXF, včetně možností pro export kót, sítí konečných prvků a deformovaných tvarů.
The image displays the AutoCAD DXF import settings in RFEM 6.
V tomto příspěvku uvádíme podrobný přehled funkcí pro import z programů RFEM 6 a RSTAB 9 do souborů AutoCAD/DXF.
Modell eines Stahlbetonbalkens, der durch Kriechen und Schwinden beeinflusst wird
Tento odborný příspěvek se zabývá přímou analýzou deformací železobetonového nosníku se zohledněním dlouhodobých účinků dotvarování a smršťování. Přímý výpočet podle Eurokódu 2 (EN 1992-1-1, Kapitola 7.4.3) je vysvětlen na prostém nosníku. Zvláštní pozornost je věnována tahovému zpevnění, chování ve stavu s trhlinami na základě součinitele rozdělení (parametr poškození) a zohlednění smršťování a dotvarování.
Screenshoty
Funkce programů
Asistent pro zatížení sněhem s možnostmi pro přesažený sníh a zachytávače sněhu podle Eurokódu

V generátoru zatížení sněhem lze při generování zatížení sněhem podle Eurokódu zohlednit sněhové převisy a sněhové zábrany.

Die Bauzustandsanalyse ermöglicht die Anpassung von Eigenschaften wie Stäben und Flächen in verschiedenen Bauphasen.

V addonu Analýza fází výstavby (CSA) máte možnost upravovat vlastnosti objektů a posouzení prutů, ploch atd. v jednotlivých fázích výstavby.

Ange zobrazení deformací modelu v okně Průběh výpočtu programu.

Během výpočtu lze v okně Průběh výpočtu graficky zobrazit deformaci modelu pro jednotlivé kroky výpočtu.

Simulace zatížení větrem na konstrukcích s volitelnými povlaky prutů

Při simulaci větru je možné zohlednit opláštění prutů (např. od zatížení námrazou).

Často kladené dotazy (FAQ)

Pro svoji grafickou kartu NVIDIA mám na výběr mezi ovladači z „Production Branch“ a „New Feature Branch“. Který ovladač je nejvhodnější pro RFEM/RSTAB?
Je možné rychle odhadnout, zda je použitá síť dostatečně jemná?
Proč se minimální a maximální hodnoty celkového posunu neshodují s tvary deformací při práci s kombinacemi výsledků?
Je v programu RFEM 5 kontakt mezi plochami?
Mohu v modelu zobrazit souřadnice uzlů?
Byl již modul RF-TOWER z programu RFEM 5 implementován do programu RFEM 6?
Projekty zákazníků