226x

2020-06-27

Zginanie plastyczne cienkiej płyty pod obciążeniem ciągłym

Opis prac

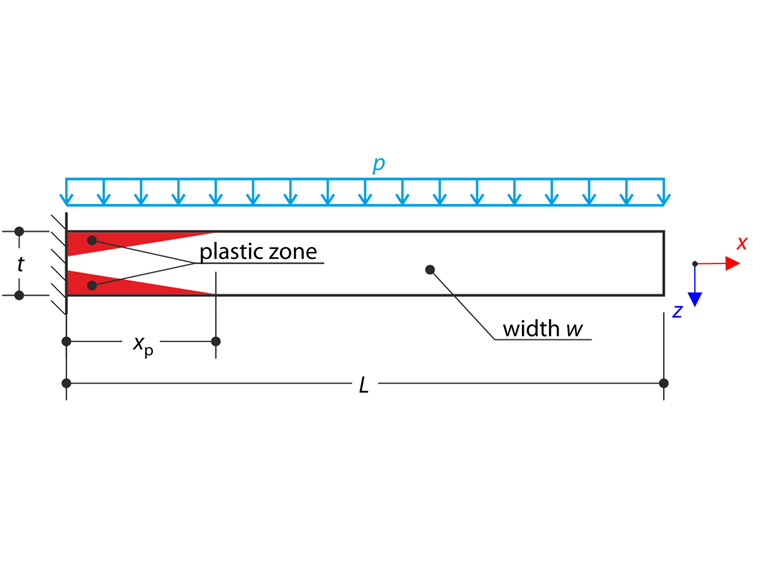
Cienka płyta jest w pełni zamocowana na lewym końcu i poddana równomiernemu naciskowi. W tym przykładzie uwzględniane są niewielkie odkształcenia, a ciężar własny jest pomijany. Problem opisano za pomocą poniższego zestawu parametrów. Określ maksymalne ugięcie u_z,max.

Materiał	Sprężysto-plastyczny	Moduł sprężystości	E	210000.000	MPa
		współczynnik Poissona	ν	0.000	-
		Moduł ścinania	G	105000.000	MPa
		Granica plastyczności	f_y	40,000	MPa
Geometria	Płyta	obwiednia	L	1,000	m
		Szerokość	w	0,050	m
		Grubość	t	0,005	m
Obciążenie		Równomierne ciśnienie	p	2,750	kPa

Zginanie plastyczne - obciążenie ciągłe

Rozwiązanie analityczne

Najpierw omówiono wielkości obciążenia. Moment M_e w chwili wystąpienia pierwszej plastyczności oraz moment graniczny M_p w chwili, gdy konstrukcja staje się przegubem plastycznym są obliczane w następujący sposób:

M_{e} = 2 \int_{0}^{t / 2} σ (z) zw dz = 2 \int_{0}^{t / 2} \frac{2 f_{y}}{t} z^{2} w dz = \frac{f_{y} {wt}^{2}}{6}

Moment sprężysty

M_{p} = 2 \int_{0}^{t / 2} σ (z) zw dz = 2 \int_{0}^{t / 2} f_{y} zw dz = \frac{f_{y} {wt}^{2}}{4}

Graniczny moment plastyczny

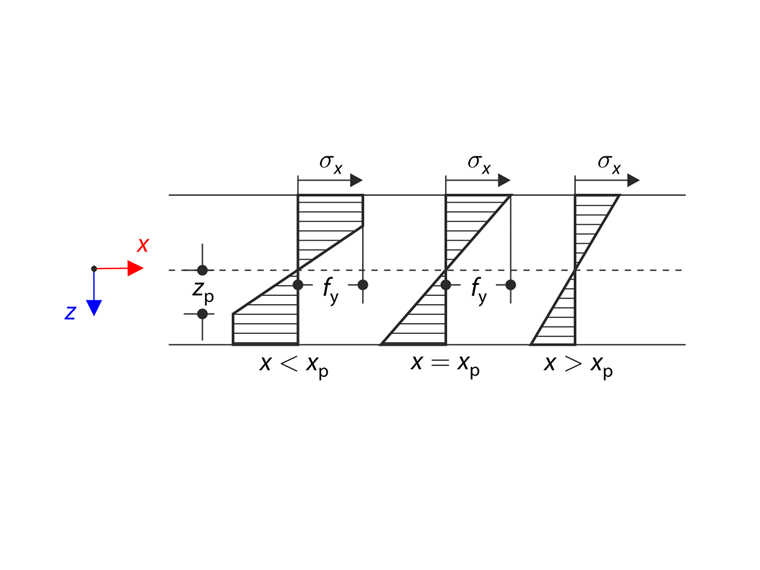
Płyta jest wprowadzana w stan sprężysto-plastyczny pod wpływem ciśnienia p. Naprężenie zginające jest definiowane według następującego wzoru:

σ_{x} (x, z) = - κ (x) Ez

naprężenie zginające

gdzie κ jest krzywizną. Długość strefy sprężysto-plastycznej jest opisana przez parametr x_p. Wielkość naprężenia zginającego na powierzchni jest równa wytrzymałości plastycznej f_y w punkcie x_p, patrz poniższy schemat.

Rozkład naprężeń zginających

Moment sprężysto-plastyczny M_ep (siła wewnętrzna) musi być równy momentowi zginającemu M (siła zewnętrzna). Krzywizna κ_p w strefie sprężysto-plastycznej wynika z tej równości.

κ_{p} = \frac{1}{E} \sqrt{\frac{\frac{f_{y}^{3} w}{3}}{- \frac{q (L - x)^{2}}{2} + \frac{f_{y} t^{2} w}{4}}}

Krzywizna w strefie sprężysto-plastycznej

u_{z, \max} = \int_{0}^{x_{p}} κ_{p} (L - x) dx + \int_{x_{p}}^{L} κ_{e} (L - x) dx = 83.117 + 83.117 = 166.234 mm

Maksymalne ugięcie wspornika

Ustawienia RFEM

Modelowany w RFEM 5.26 i RFEM 6.01
Rozmiar elementu wynosi l_FE =0,020 m
W przypadku modeli bryłowych stosowane jest zagęszczenie siatki na całej grubości (6 elementów na grubość)
Uwzględniana jest analiza geometrycznie liniowa
Liczba przyrostów wynosi 5
Sztywność prętów na ścinanie jest pominięta

Wyniki

Model	Rozwiązanie analityczne	RFEM 5		RFEM 6
Model	u_z,max [mm]	u_z,max [mm]	Stosunek [-]	u_z,max [mm]	Stosunek [-]
Izotropowy Plastyczny 1D	166,234	166.214	1,000	166.018	0,999
Izotropowy plastyczny 2D/3D, płytowy		162.987	0,980	162,960	0,980
Izotropowy nieliniowo sprężysty 2D/3D, płytowy, von Mises		165.730	0.997	165.700	0.997
Izotropowy nieliniowy sprężysty 2D/3D, płytowy, Tresca		166.998	1.005	166.969	1.004
Izotropowy plastyczny 2D/3D, bryła		160.601	0.966	162.429	0.977
Izotropowy, nieliniowy, sprężysty 2D/3D, bryłowy, von Mises		163.003	0,981	165.593	0,996
Izotropowy, nieliniowy, sprężysty 2D/3D, bryłowy, Tresca		168.725	1,015	169.691	1,021
Izotropowy, nieliniowy, sprężysty 1D		166.214	1,000	166.018	0,999

Uwaga: Odchyłka wyników wynika również z różnicy między obliczoną analitycznie a obliczoną numerycznie stałą skręcania.

428x

Przykład weryfikacyjny 0017 | 1

Odniesienia

Lubliner, J. (1990). Teoria plastyczności. Nowy Jork: Macmillana.

;