ASCE 7-22 i NBC 2020 Sejsmiczne uwagi P-Delta w RFEM 6

ASCE 7-22 i P-Delta Effects

ASCE 7-22 Norma [1], rozdz. 12.9.1.6 odnosi się do rozdz. 12.8.7 [1], zgodnie z którym uwzględnianie P-delta nie jest wymagane, jeżeli współczynnik stateczności (θ) określony za pomocą poniższego równania jest równy lub mniejszy niż 0,10.

Norma dalej stanowi, że θ nie powinno przekraczać mniejszej z wartości θ_max, podanej za pomocą poniższego równania, ponieważ konstrukcja jest potencjalnie niebezpieczna i powinna zostać przeprojektowana.

Jeżeli 0,10 < θ ≤ θ_max, jest to dozwolone dla przemieszczeń, a siły prętowe należy pomnożyć przez współczynnik 1,0/(1-θ). Alternatywnie, efekty P-delta można uwzględnić w analizie automatycznej, tam gdzie nadal obowiązują ograniczenia θ_max.

NBC 2020 i efekty P-Delta

W Wysłane. 4.1.8.3.8.c NBC 2020 [2], podano tylko krótki wymóg, aby uwzględnić efekty przechyłowe wynikające z interakcji obciążeń grawitacyjnych z odkształconą konstrukcją. Jednak w Komentarzu do NBC 2015 [3] znajdują się dalsze wyjaśnienia, podobnie jak w normie ASCE 7, w której współczynnik stateczności (θ_x ) na poziomie x należy obliczać przy użyciu poniższego równania.

Jeżeli θ_x jest mniejsze niż 0,10, efekty P-delta można zignorować. Jeżeli θ_x jest większe niż 0,40, konstrukcję należy przeprojektować, ponieważ jest uznawana za niebezpieczną podczas ekstremalnych trzęsień ziemi. Dla 0,10 ≤ θ_x ≤ 0,40, siły i momenty wywołane trzęsieniem ziemi można pomnożyć przez współczynnik (1+θ_x ), aby uwzględnić P-delta. Współczynnik ten nie musi być stosowany do przemieszczeń.

Przybliżone uwzględnienie efektów P-Delta ze współczynnikami amplifikacji

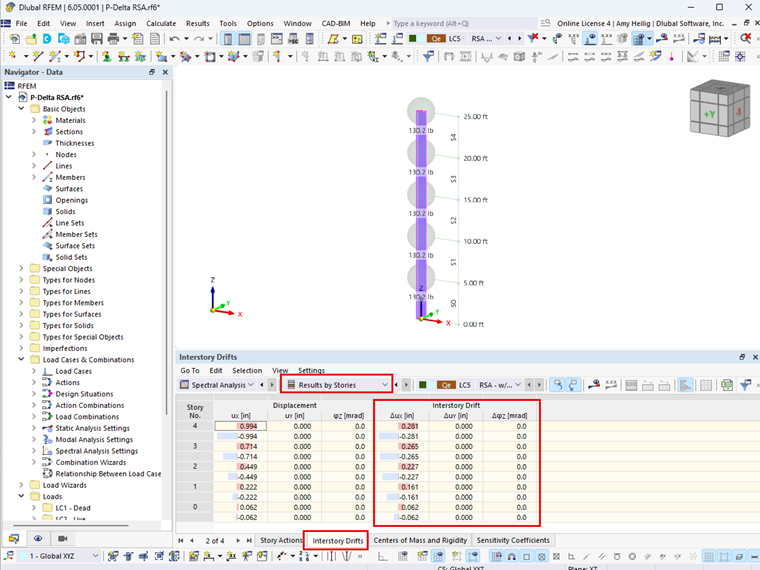
Wartość współczynnika stateczności należy obliczyć w obu ortogonalnych kierunkach poziomych, aby określić, czy parametr P-delta stanowi problem. Wymagany ślizg kondygnacji, Δ, niezbędny do obliczenia współczynnika stateczności zarówno w ASCE 7-22, jak i NBC 2020, jest teraz podawana automatycznie w programie RFEM 6 z rozszerzeniem Projektowanie budowlane. Dla każdego poziomu kondygnacji w tabeli wyników zostanie uwzględniony odpowiedni ślizg kondygnacji, jak pokazano na rysunku 01.

Jeżeli jeden lub oba kierunki wymagają uwzględnienia efektów drugiego rzędu w podanych zakresach, można łatwo uwzględnić współczynnik 1,0/(1-θ) z ASCE 7-22 lub (1+θ_x ) z NBC 2020. RFEM 6 i rozszerzenie Analiza spektrum odpowiedzi. Wszystkie wypadkowe siły i/lub ugięcia zostaną zwiększone o zadaną wartość.

Dokładniejsze uwzględnienie efektów P-Delta dzięki geometrycznej macierzy sztywności

Chociaż efekty wtórne można oszacować za pomocą powyższych współczynników, jest to bardziej konserwatywne podejście. W sytuacjach, w których występują duże kondygnacje, lub konieczne jest obliczenie efektów P-delta z dokładniejszym podejściem, wpływ sił osiowych można aktywować w rozszerzeniu Analiza spektrum odpowiedzi.

Podczas przeprowadzania analizy dynamicznej typowe nieliniowe obliczenia iteracyjne dla efektów drugiego rzędu w przypadku analizy statycznej nie są już stosowane. Problem musi zostać zlinearyzowany, co jest realizowane poprzez aktywację macierzy sztywności geometrycznej podczas analizy. Dzięki temu podejściu zakłada się, że obciążenia pionowe nie zmieniają się pod wpływem oddziaływań poziomych, a odkształcenia są niewielkie w porównaniu z całkowitymi wymiarami konstrukcji [2].

Ideą macierzy sztywności geometrycznej jest efekt usztywnienia naprężeń. Rozciągające siły osiowe prowadzą do zwiększenia sztywności pręta na zginanie, a osiowe siły ściskające do zmniejszenia sztywności na zginanie. Można to łatwo przedstawić na przykładzie kabla lub smukłego pręta. W przypadku działania siły rozciągającej sztywność na zginanie jest znacznie większa niż w przypadku działania siły ściskającej. W przypadku ściskania, pręt ma bardzo małą sztywność na zginanie, aby wytrzymać przyłożone obciążenie boczne.

Geometryczną macierz sztywności K_g można wyprowadzić z warunków równowagi statycznej.

Dla uproszczenia wyświetlane są tylko stopnie swobody przemieszczenia poziomego. Pokazana pochodna jest oparta na podejściu momentu krytycznego wynikającego z zastosowania liniowego przemieszczenia. Jest to uproszczenie dla elementu zginanego i dokładne założenie dla elementu kratownicy. Zwróć uwagę, że macierz zależy tylko od długości elementu i siły osiowej.

Bardziej precyzyjne wyznaczenie macierzy sztywności geometrycznej dla belek zginanych można uzyskać, stosując podejście przemieszczeń sześciennych lub poprzez analityczne rozwiązanie równania różniczkowego linii zginania. Więcej informacji na temat teorii i pochodnych można znaleźć w Werkle [4].

Geometryczna macierz sztywności K_g zostaje dodana do macierzy sztywności układu K , a tym samym otrzymuje się zmodyfikowaną macierz sztywności K_mod :

K_mod = K + K_g

W przypadku ściskania sił normalnych prowadzi to w konsekwencji do zmniejszenia sztywności.

Przykład modyfikacji sztywności geometrycznej P-Delta w RFEM 6

W programie RFEM 6 zastosowano redukcję sztywności z wykorzystaniem geometrycznej macierzy sztywności do uwzględnienia efektów drugiego rzędu (P-Delta) w analizie spektrum odpowiedzi. Pręt ma przekrój W 12x26 i materiał A992 o I_y = 204 in⁴ i E = 29000 ksi. Każdy z (5) poziomów kondygnacji ma wysokość 5 stóp, co daje całkowitą wysokość 25 stóp.

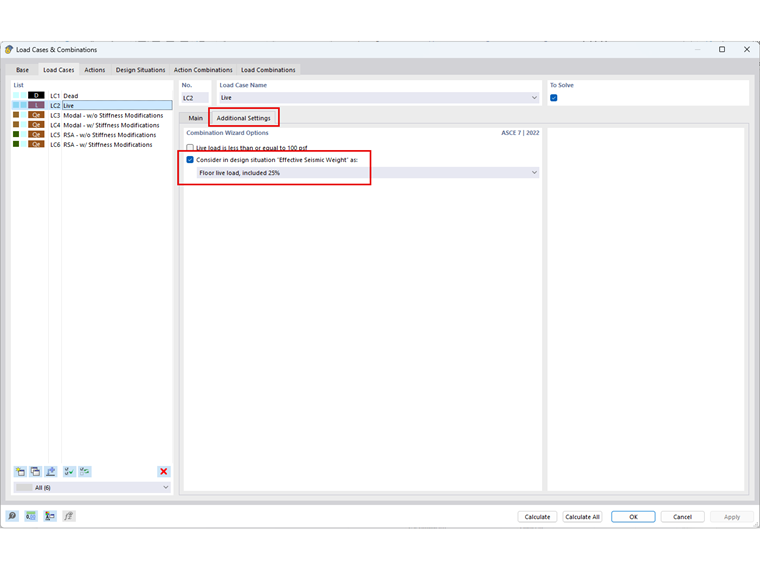
Pomijając ciężar własny, w KO 1: Obciążenie zmienne oraz stałe 3 kN na każdym poziomie w ramach PO2: Na żywo. Dodatkowe ustawienia w PO2 są aktywowane w celu automatycznego uwzględnienia 25% obciążenia zmiennego dla kombinacji mas.

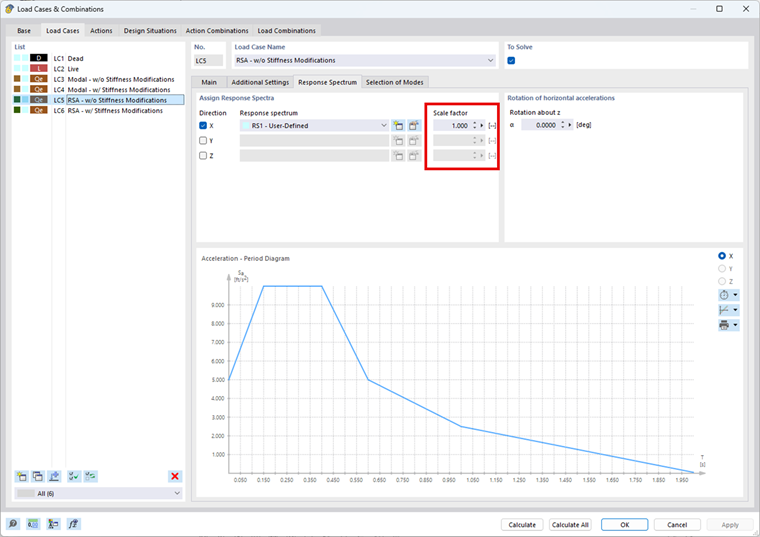
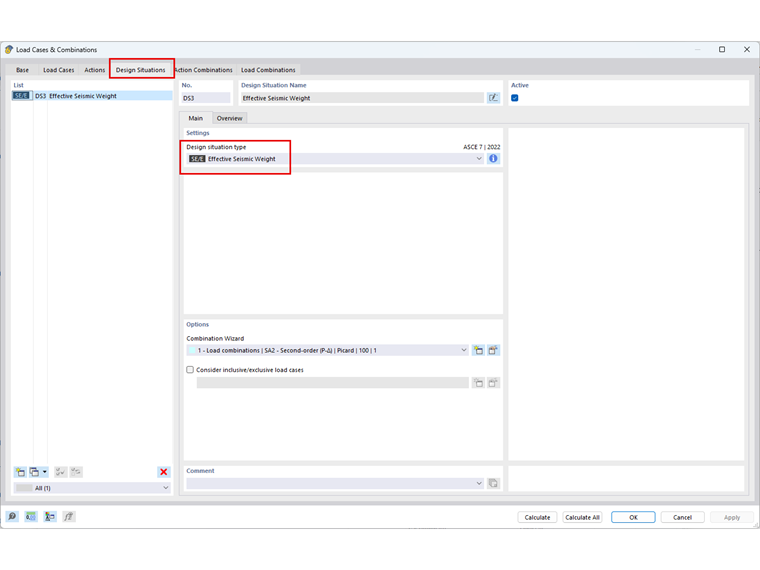
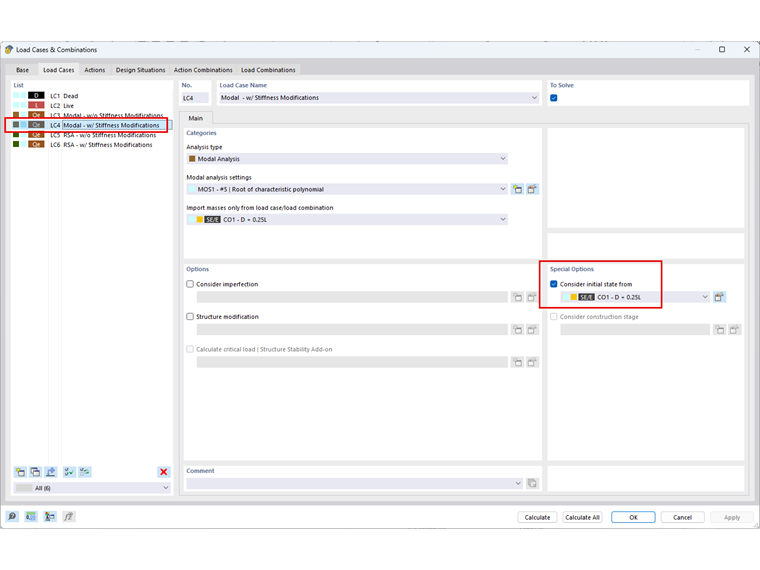
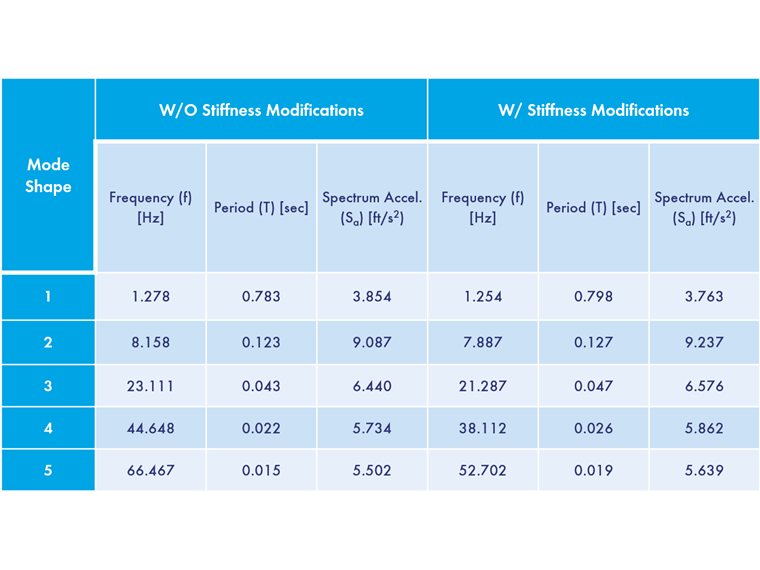
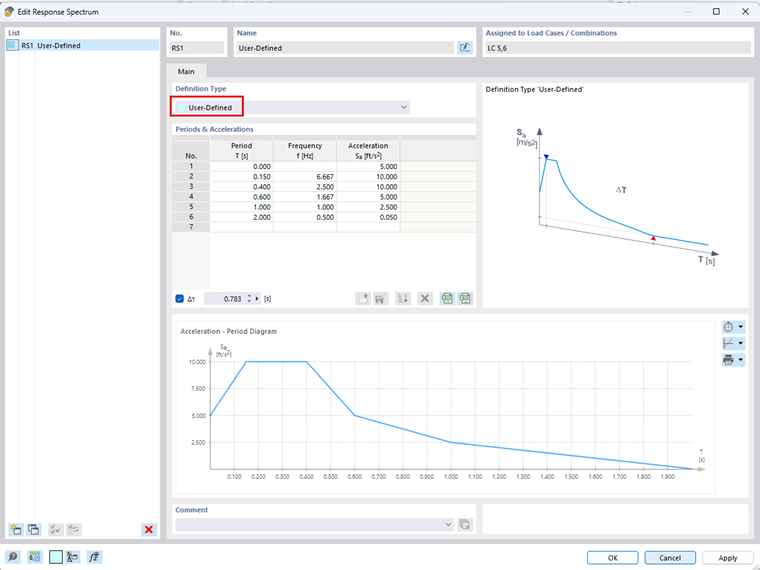
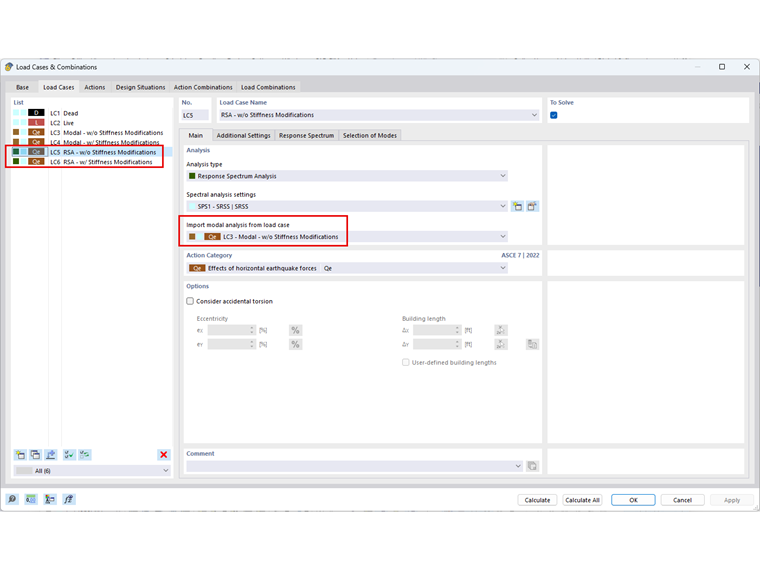
Sytuacja obliczeniowa DS1: Efektywna masa sejsmiczna jest zdefiniowana w celu automatycznego tworzenia kombinacji mas KO1: D + 0,25L. Po przeliczeniu mas, uwzględniane jest łącznie 1000 kg na każdym poziomie w kierunku X do dalszej analizy sejsmicznej.

Rozszerzenie Analiza modalna obliczy kształty drgań i efektywne masy modalne konstrukcji. Możliwe jest uwzględnienie stanu początkowego, który spowoduje zastosowanie modyfikacji sztywności na podstawie zdefiniowanych przypadków obciążeń i kombinacji obciążeń. Zdefiniowane są dwa przypadki obciążeń analizy modalnej. Pierwszym z nich jest PO3: Modalna – bez modyfikacji sztywności, aby przeprowadzić analizę modalną bez modyfikacji sztywności. Dla PO4: Modalne – z modyfikacjami sztywności, opcja Uwzględnij stan początkowy jest aktywowana. Importowany przypadek obciążenia lub kombinacja obciążeń powinna uwzględniać największe ściskające obciążenia osiowe konstrukcji. W tym przykładzie zastosowano kombinację mas KO1 w celu przybliżenia efektów drugiego rzędu przy użyciu modyfikacji sztywności geometrycznej. Poniższa tabela przedstawia obliczone częstotliwości drgań własnych (f) [Hz] i okresy drgań własnych (T) [s] z uwzględnieniem macierzy sztywności geometrycznej '''K_g''' i bez niej. Multimodalna analiza spektrum odpowiedzi odnosi się do częstotliwości drgań własnych konstrukcji w celu określenia wartości przyspieszenia na podstawie zdefiniowanego spektrum odpowiedzi. Na podstawie tych wartości przyspieszenia program określa siły wewnętrzne spektrum odpowiedzi. W tym przykładzie zdefiniowano spektrum odpowiedzi zdefiniowane przez użytkownika, jak pokazano poniżej. Wartości przyspieszenia S_a [ft/s² ] wyznaczone na podstawie zdefiniowanego przez użytkownika spektrum odpowiedzi dla każdej wartości własnej są wymienione w powyższej tabeli. Aby zapewnić prawidłowe przypisanie zmodyfikowanych częstotliwości, żądaną analizę modalną należy wybrać podczas definiowania przypadku obciążenia spektrum odpowiedzi. Oznacza to, że jeżeli analiza spektrum odpowiedzi ma uwzględniać zmiany sztywności geometrycznej, należy odnieść się do odpowiedniej analizy modalnej z wcześniej zdefiniowanymi zmianami sztywności. W przypadku stosowania osiowych sił ściskających uwzględnienie macierzy sztywności geometrycznej prowadzi do niższych częstotliwości drgań własnych konstrukcji. Jak widać na tym przykładzie, może to powodować niższe wartości przyspieszenia S_a. Sama modyfikacja częstotliwości drgań własnych nie jest wystarczająca do uwzględnienia teorii drugiego rzędu. W rzeczywistości może to prowadzić do mniejszych wyników, które mogą być nieprawidłowe. Dlatego ważne jest, aby do obliczania sił wewnętrznych i odkształceń w konstrukcji stosować zmodyfikowaną macierz sztywności. W przypadku analizy spektrum odpowiedzi w programie RFEM zmodyfikowana sztywność z analizy modalnej jest automatycznie stosowana do określenia wyników analizy spektrum odpowiedzi. Odkształcenia, siły wewnętrzne i reakcje podporowe wyznaczone w analizie spektrum odpowiedzi, z i bez geometrycznej macierzy sztywności, pokazano na rysunku 08. Uwzględnienie macierzy sztywności geometrycznej prowadzi do większych odkształceń i sił wewnętrznych. Wynikające z tego obciążenia podporowe są jednak nieco mniejsze, jeśli wziąć pod uwagę macierz sztywności geometrycznej.