Lissage des efforts internes des surfaces dans RFEM

Vous pouvez sélectionner différentes options dans le programme pour afficher les résultats non lissés ou lissés. Elles sont décrites dans le manuel de RFEM. Les options de lissage permettant d'évaluer les efforts internes et les contraintes de surface sont également expliquées dans cet article technique de notre base de connaissance. L'exemple de cet article illustre la manière dont les efforts internes des éléments finis pour le lissage sont utilisés pour déterminer les valeurs. Outre la position des éléments finis, la théorie des plaques (Mindlin ou Kirchhoff) joue un également rôle dans ce processus.

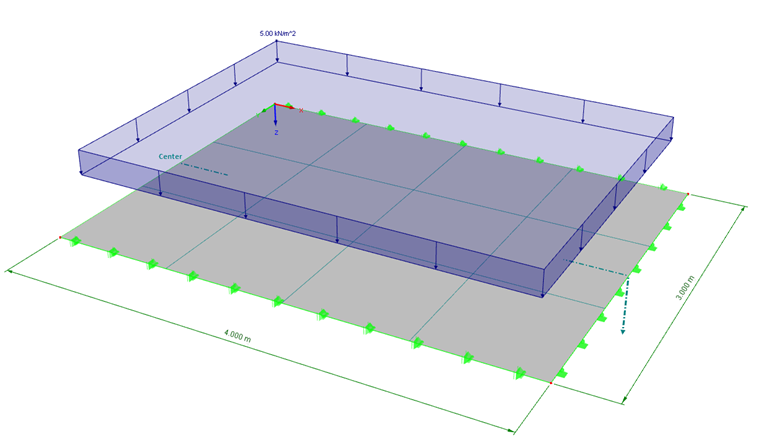
Exemple : Plaque selon la théorie de Mindlin et Kirchhoff

Exemple

Un modèle de plaque 2D de dimensions 4 m ⋅ 3 m a été créée. La plaque est articulée des deux côtés des lignes de contour les plus courtes. La rotation des lignes de contour plus longues est limitée par une contrainte. Le coefficient de Poisson du matériau est défini sur zéro pour éviter les effets de déformation transversaux. Une épaisseur de plaque de 80 cm est sélectionnée pour comparer la détermination des efforts internes selon les théories de Kirchhoff et Mindlin sur la flexion de plaque. Un rapport d/L = 0,2 est donné dans la zone limite entre les deux théories sur la flexion (voir cet article de notre FAQ).

La taille du maillage EF est définie sur 1 m à des fins de simplification et il y a donc 4 ⋅ 3 éléments finis.

Une charge de p = 5 kN/m² agit sur la plaque et le poids propre n'est pas appliqué dans le cas de charge.

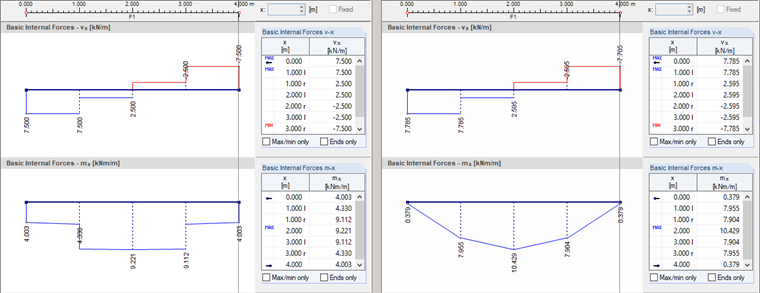
Efforts internes non lissés

Les résultats du noyau de calcul pour les efforts internes v_x et m_x sont considérés pour une section longitudinale au centre de la plaque. La répartition des efforts internes non lissés élément par élément peut être visualisée à l'aide de l'option d'affichage « Non continue ». Les diagrammes de la Figure 02 obtenus selon les théories de Mindlin et Kirchhoff sur la flexion sont alors disponibles.

Résultats non lissés selon Mindlin (à gauche) et Kirchhoff (à droite)

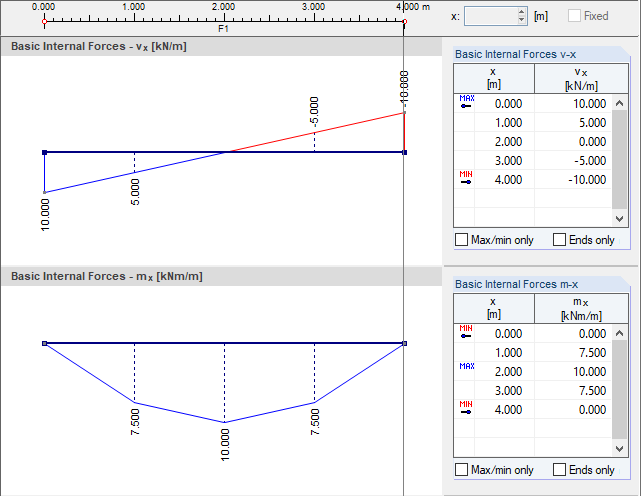
Lissage standard des nœuds internes

Pour les nœuds EF situés dans une surface, la moyenne arithmétique est d'abord calculée à partir des valeurs nodales des éléments finis adjacents. Pour appliquer cette méthode, les éléments doivent se trouver dans une surface et du même côté d'une ligne interne. Le nœud ne doit pas être un nœud dans la surface ne doit pas être défini par l'utilisateur.

Les valeurs sont les suivantes en interne (le résultat de cette étape n'est pas disponible pour la sortie) pour l'emplacement de discontinuité à x = 1,00 m :

Mindlin :

Kirchhoff :

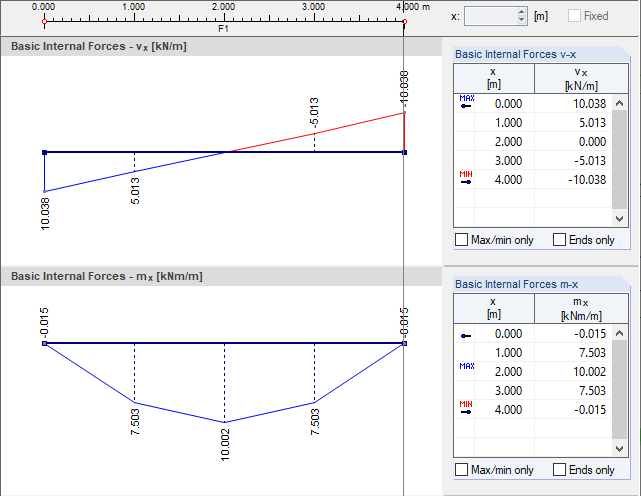
Lissage des nœuds de bord

Aucun élément fini qui pourrait être utilisé pour la moyenne des valeurs nodales ne se trouve au niveau des bords d'une surface (option de lissage « Continue dans les surfaces ») ou d'un modèle (« Continue au total »). Une approche différente en deux étapes est donc appliquée.

Dans un premier temps, les valeurs moyennes sont calculées pour les nœuds qui ne se trouvent pas au bord d'une surface ou du modèle. Les valeurs des nœuds situés sur les bords sont calculées de sorte que les valeurs d'origine au centre des éléments finis soient conservées. Les valeurs moyennes des nœuds de bord sont déterminées lors de la seconde étape.

Pour le nœud à x = 0,00 m, on obtient les valeurs suivantes :

Mindlin :

Kirchhoff :

Efforts tranchants

Selon la théorie de Mindlin, les efforts tranchants sont calculés comme la première dérivée de la flèche.

Ces valeurs sont déterminées par le noyau de calcul et utilisées directement. Le lissage des efforts tranchants est ensuite effectué comme décrit ci-dessus, en fonction de la position du nœud EF dans la surface.

Selon la théorie de Kirchhoff, les efforts tranchants sont calculés comme la troisième dérivée de la flèche.

Cette détermination à l'aide de la troisième dérivée diminue considérablement la précision. Par conséquent, les efforts tranchants du noyau de calcul ne sont pas utilisés, mais déterminés à partir des dérivations des moments à l'aide d'une approche améliorée.

Les moments m_x, m_y et m_xy dans les équations représentent les valeurs lissées qui sont déterminées selon les méthodes décrites ci-dessus. Les valeurs des efforts tranchants sont donc plus précises que celles calculées avec le noyau de calcul.

Moments

Bien que les valeurs des moments dans les points d'intégration correspondent aux valeurs théoriques, l'extrapolation diminue la précision lors de l'utilisation de la fonction paraboloïde hyperbolique pour le lissage. Un paraboloïde hyperbolique n'est qu'une approximation de la répartition des moments dans l'élément. Un algorithme amélioré est ainsi utilisé pour remplacer cette extrapolation par une méthode intégrée avancée de l'effort tranchant. On suppose que la répartition de l'effort tranchant dans l'élément surfacique a la forme d'un paraboloïde hyperbolique (surface du second ordre). L'intégrale de cette surface représente donc une surface du troisième ordre, qui affiche la répartition des moments avec une meilleure précision.

Cette approche correspond aux équations de détermination des efforts tranchants par la dérivée des moments ci-dessus. Les moments sont ensuite déterminés à l'aide des équations suivantes :

Les constantes d'intégration m_x,0 et m_y,0 sont calculées à partir des conditions de la valeur au centre de l'élément.

S représente la surface de l'élément.

Les valeurs des efforts internes sont déterminées à l'aide des méthodes décrites ci-dessus et les intégrales par une intégration numérique. Les moments ainsi déterminés sont ensuite lissés selon la méthode appliquée pour les nœuds internes ou les nœuds de bord.

On obtient les valeurs suivantes pour cet exemple selon la théorie de Mindlin :

Premier élément :

Second élément :

Diagrammes lissés des efforts internes v-x et m-x selon Mindlin

On obtient les valeurs suivantes pour cet exemple selon la théorie de Kirchhoff :

Premier élément :

Second élément :

Diagrammes lissés des efforts internes v-x et m-x selon Kirchhoff

Les étapes décrites ci-dessus sont exécutées une à une dans le programme lors du processus de lissage. Les valeurs lissées peuvent être affichées graphiquement à l'aide de l'option « Continu dans les surfaces ».