Livellamento delle forze interne di superficie in RFEM

È possibile selezionare diverse opzioni nel programma per visualizzare i risultati non smussati o smussati. Sono descritti nel manuale di RFEM.

• Manuale online per il programma RFEM 5 (in inglese)

Le opzioni di smussamento per valutare le forze interne delle superfici e le tensioni sono spiegate anche in questo articolo tecnico.

• KB 001571 | Diagramma delle forze interne/Tensioni superficiali - Opzioni di smussamento

Il seguente articolo utilizza un esempio per illustrare come le forze interne negli elementi finiti per lo smussamento vengono utilizzate per determinare i valori. Oltre alla posizione di un elemento finito, la teoria delle piastre - Mindlin o Kirchhoff - gioca un ruolo in questo processo.

Esempio: piastra secondo Mindlin e Kirchhoff

1 Esempio

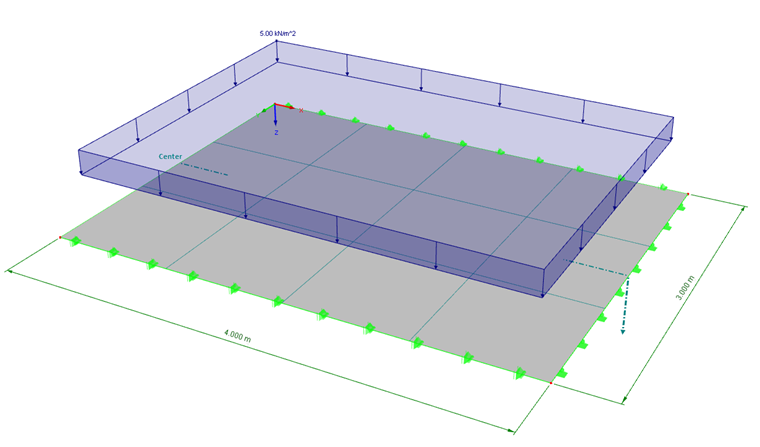
Una piastra con le dimensioni 4 m ⋅ 3 m viene creata come modello bidimensionale. La piastra è incernierata su entrambi i lati alle linee di contorno più brevi. La rotazione delle linee di contorno più lunghe è vincolata da un vincolo. Per evitare effetti di deformazione trasversale, il rapporto di Poisson's del materiale è impostato su zero. Per confrontare la determinazione delle forze interne secondo le teorie di flessione della piastra di Kirchhoff e Mindlin, viene selezionato uno spessore della piastra di 80 cm. Pertanto, il rapporto d/L = 0.2 è dato nella zona limite tra le due teorie di flessione (vedi FAQ 003158).

• FAQ | È sufficiente eseguire il calcolo con elementi di superficie o è meglio utilizzare elementi solidi?

Per semplificare, la dimensione della mesh della mesh EF è impostata su 1 m. Quindi, ci sono 4 ⋅ 3 elementi finiti.

Un carico di p = 5 kN/m² agisce sulla piastra. Il peso proprio non è applicato nel caso di carico.

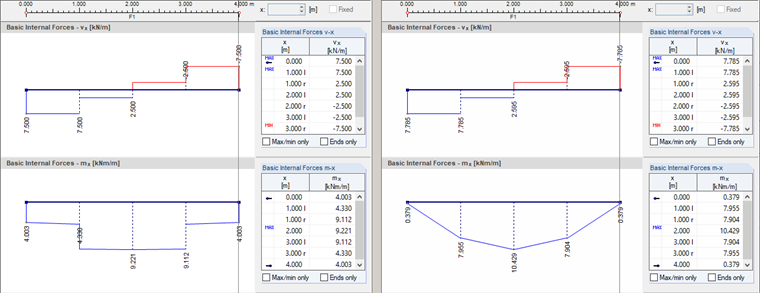
Forze interne non smussate

I risultati del kernel di calcolo per le forze interne v_x e m_x sono considerati per una sezione longitudinale che corre al centro della piastra. La distribuzione delle forze interne non smussate elemento per elemento può essere rappresentata dall'opzione di visualizzazione "Non continua". Secondo le teorie di flessione di Mindlin e Kirchhoff, sono disponibili i diagrammi mostrati nell'immagine 02.

2 Risultati non livellati secondo Mindlin (a sinistra) e Kirchhoff (a destra)

Smussamento standard per nodi interni

Per i nodi EF che si trovano all'interno di una superficie, la media aritmetica è prima formata dai valori dei nodi degli elementi finiti adiacenti. Per questo approccio, gli elementi devono giacere su una superficie e sullo stesso lato di una possibile linea interna. Il nodo non deve essere un nodo definito dall'utente nella superficie.

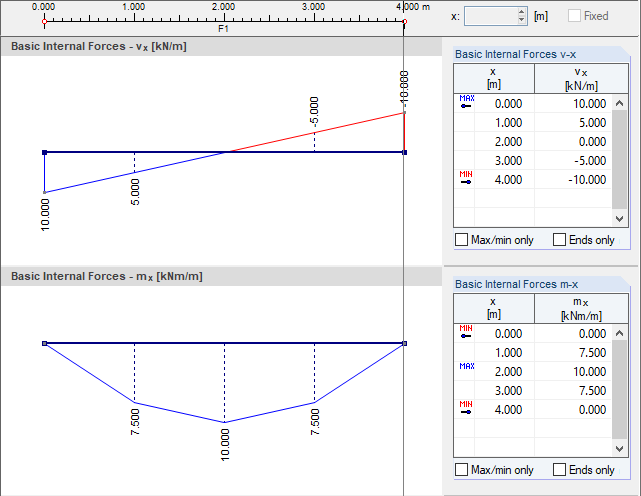
Per la posizione della discontinuità a x = 1,00 m, questi valori sono i seguenti internamente (il risultato di questo passaggio non è disponibile per l'output).

• Mindlin:
  $${\mathrm{v}}_{\mathrm{x}}\left(1\right) = \frac{7.5 · 2.5}{2} = 5$$

  $${\mathrm{m}}_{\mathrm{x}}\left(1\right) = \frac{8.772 · 5.351}{2} = 7.061$$

  Smussamento standard per nodi interni secondo Mindlin
• Kirchhoff:
  $${\mathrm{v}}_{\mathrm{x}}\left(1\right) = \frac{7.785 · 2.595}{2} = 5.19$$

  $${\mathrm{m}}_{\mathrm{x}}\left(1\right) = \frac{7.954 · 7.904}{2} = 7.929$$

  Smussamento standard per nodi interni secondo Kirchhoff

Smussamento per nodi del bordo

Ai bordi di una superficie (opzione di smussamento "Continuo nelle superfici") o di un modello ("Totale continuo"), non ci sono elementi finiti adiacenti che potrebbero essere utilizzati per la media dei valori dei nodi. Pertanto, viene utilizzato un approccio diverso, che viene eseguito in due fasi.

Nella prima fase, i valori medi sono calcolati per quei nodi che non si trovano sul bordo di una superficie o del modello. I valori dei nodi ai bordi sono calcolati in modo tale che i valori originali rimangano al centro degli elementi finiti. Nella seconda fase, vengono determinati i valori medi per i nodi del bordo.

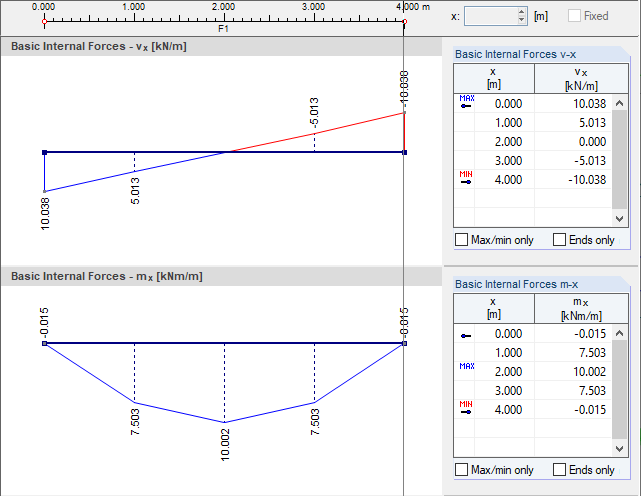
I seguenti valori risultano per il nodo del bordo a x = 0,00 m.

• Mindlin:
  $${\mathrm{v}}_{\mathrm{x}}\left(0\right) = 7.5 · (7.5 - 5) = 10$$

  $${\mathrm{m}}_{\mathrm{x}}(0.5) = \frac{5.351 · 2.982}{2} = 4.167$$

  $${\mathrm{m}}_{\mathrm{x}}\left(0\right) = 4.167 · (4.167 - 7.061) = 1.272$$

  Smussamento per nodi del bordo secondo Mindlin
• Kirchhoff:
  $${\mathrm{v}}_{\mathrm{x}}\left(0\right) = 7.785 · (7.785 - 5.19) = 10.381$$

  $${\mathrm{m}}_{\mathrm{x}}(0.5) = \frac{7.954 · 0.379}{2} = 4.167$$

  $${\mathrm{m}}_{\mathrm{x}}\left(0\right) = 4.167 · (4.167 - 7.929) = 0.404$$

  Smussamento per nodi di bordo secondo Kirchhoff

Taglio

Secondo Mindlin, le forze di taglio sono calcolate come la derivata prima dell'inflessione.

Questi valori sono determinati dal kernel di calcolo e utilizzati direttamente. Lo smussamento delle forze di taglio viene quindi eseguito come descritto sopra, a seconda della posizione del nodo EF nella superficie.

Nella teoria della flessione secondo Kirchhoff, le forze di taglio sono calcolate come la terza derivata dell'inflessione.

Questa determinazione del valore utilizzando la derivata terza risulta in una notevole perdita di precisione. Per questo motivo, le forze di taglio del nucleo di calcolo non vengono utilizzate, ma determinate dalle derivazioni dei momenti con un approccio migliorato.

I momenti m_x, m_y e m_xy nelle equazioni rappresentano i valori smussati determinati secondo i metodi sopra descritti. Ciò si traduce in valori più accurati per le forze di taglio rispetto al loro calcolo con il kernel di calcolo.

Momenti

Mentre i valori del momento nei punti di integrazione corrispondono ai valori teorici, l'estrapolazione porta a una perdita di precisione quando si utilizza la funzione paraboloide iperbolica per lo smussamento. Un paraboloide iperbolico approssima solo la distribuzione del momento nell'elemento. Per questo motivo, viene utilizzato un algoritmo migliorato che sostituisce l'estrapolazione con un metodo avanzato della forza di taglio integrale. Poiché si presume che la distribuzione della forza di taglio nell'elemento di superficie sia la forma di un paraboloide iperbolico (superficie del secondo ordine), l'integrale di questa superficie rappresenta una superficie del terzo ordine, che visualizza la distribuzione del momento con maggiore precisione.

Questo approccio corrisponde alle equazioni sopra descritte per determinare le forze di taglio tramite le derivate dei momenti. I momenti sono quindi determinati con le seguenti equazioni.

Le costanti di integrazione m_x,0 e m_y,0 sono calcolate dalle condizioni del valore al centro dell'asta.

I valori delle forze interne sono determinati con i metodi sopra descritti; gli integrali, mediante un'integrazione numerica. I momenti così determinati vengono quindi smussati secondo il metodo per nodi interni o nodi di bordo.

Nella teoria della flessione secondo Mindlin, i seguenti valori risultano in questo esempio.

• Primo elemento:
  $${\mathrm{v}}_{\mathrm{x}}\left(\mathrm{x}\right) = 10 - 5 \mathrm{x}$$

  $${\mathrm{m}}_{\mathrm{x}}\left(\mathrm{x}\right) = \int {\mathrm{v}}_{\mathrm{x}}\mathrm{dx} {\mathrm{m}}_{\mathrm{x},0} = 10 \mathrm{x} - \frac{5}{2} {\mathrm{x}}^2 {\mathrm{m}}_{\mathrm{x},0}$$

  $${\mathrm{m}}_{\mathrm{x},\mathrm{C}} = {\mathrm{m}}_{\mathrm{x}}(0.5) = 4.167 = {\int }_0^{1}10 \mathrm{x} - \frac{5}{2} {\mathrm{x}}^2 {\mathrm{m}}_{\mathrm{x},0} = {\left[\frac{10}{2} {\mathrm{x}}^2 - \frac{5}{6} {\mathrm{x}}^3 {\mathrm{m}}_{\mathrm{x},0}\mathrm{x}\right]}_0^1 = 4.167 {\mathrm{m}}_{\mathrm{x},0}$$

  $${\mathrm{m}}_{\mathrm{x},0} = {\mathrm{m}}_{\mathrm{x}}\left(0\right) = 4.167 - 4.167 = 0$$

  $${\mathrm{m}}_{\mathrm{x}}{\left(1\right)}^{-} = 10 - \frac{5}{2} 0 = 7.5$$

  Primo elemento che utilizza la teoria della flessione secondo Mindlin
• Secondo elemento:
  $${\mathrm{v}}_{\mathrm{x}}\left(\mathrm{x}\right) = 5 - 5 \mathrm{x}$$

  $${\mathrm{m}}_{\mathrm{x}}\left(\mathrm{x}\right) = \int {\mathrm{v}}_{\mathrm{x}}\mathrm{dx} + {\mathrm{m}}_{\mathrm{x},0} = 5 \mathrm{x} - \frac{5}{2} {\mathrm{x}}^2 + {\mathrm{m}}_{\mathrm{x},0}$$

  $${\mathrm{m}}_{\mathrm{x},\mathrm{C}} = {\mathrm{m}}_{\mathrm{x}}(1.5) = 9.167 = {\int }_0^{1}5 \mathrm{x} - \frac{5}{2} {\mathrm{x}}^2 + {\mathrm{m}}_{\mathrm{x},0} = {\left[\frac{5}{2} {\mathrm{x}}^2 - \frac{5}{6} {\mathrm{x}}^3 + {\mathrm{m}}_{\mathrm{x},0}\mathrm{x}\right]}_0^1 = 1.667 + {\mathrm{m}}_{\mathrm{x},0}$$

  $${\mathrm{m}}_{\mathrm{x},0} = {\mathrm{m}}_{\mathrm{x}}(1{)}^{+} = 9.167 - 1.667 = 7.5$$

  $${\mathrm{m}}_{\mathrm{x}}\left(1\right) = \frac{{\mathrm{m}}_{\mathrm{x}}(1{)}^{-} + {\mathrm{m}}_{\mathrm{x}}(1{)}^{+}}{2} = \frac{7.5 + 7.5}{2} = 7.5$$

  Secondo elemento utilizzando la teoria della flessione secondo Mindlin

3 Distribuzione livellata delle forze interne vx e mx secondo Mindlin

I seguenti valori sono ottenuti per la teoria della flessione secondo Kirchhoff.

• Primo elemento:
  $${\mathrm{v}}_{\mathrm{x}}\left(\mathrm{x}\right) = 10.038 - 5.025 \mathrm{x}$$

  $${\mathrm{m}}_{\mathrm{x}}\left(\mathrm{x}\right) = \int {\mathrm{v}}_{\mathrm{x}}\mathrm{dx} {\mathrm{m}}_{\mathrm{x},0} = 10.038 \mathrm{x} - \frac{5.025}{2} {\mathrm{x}}^2 {\mathrm{m}}_{\mathrm{x},0}$$

  $${\mathrm{m}}_{\mathrm{x},\mathrm{C}} = {\mathrm{m}}_{\mathrm{x}}(0.5) = 4.167 = {\int }_0^{1}10.038 \mathrm{x} - \frac{5.025}{2} {\mathrm{x}}^2 {\mathrm{m}}_{\mathrm{x},0} = {\left[\frac{10.038}{2} {\mathrm{x}}^2 - \frac{5.025}{6} {\mathrm{x}}^3 {\mathrm{m}}_{\mathrm{x},0}\mathrm{x}\right]}_0^1 = 4.182 {\mathrm{m}}_{\mathrm{x},0}$$

  $${\mathrm{m}}_{\mathrm{x},0} = {\mathrm{m}}_{\mathrm{x}}\left(0\right) = 4.167 - 4.182 = - 0.015 {\mathrm{m}}_{\mathrm{x}}{\left(1\right)}^{-} = 10.038 - \frac{5.025}{2} - 0.015 = 7.511$$

  Primo elemento utilizzando la teoria della flessione secondo Kirchhoff
• Secondo elemento:
  $${\mathrm{v}}_{\mathrm{x}}\left(\mathrm{x}\right) = 5.013 - 5.013 \mathrm{x}$$

  $${\mathrm{m}}_{\mathrm{x}}\left(\mathrm{x}\right) = \int {\mathrm{v}}_{\mathrm{x}}\mathrm{dx} + {\mathrm{m}}_{\mathrm{x},0} = 5.013 \mathrm{x} - \frac{5.013}{2} {\mathrm{x}}^2 + {\mathrm{m}}_{\mathrm{x},0}$$

  $${\mathrm{m}}_{\mathrm{x},\mathrm{C}} = {\mathrm{m}}_{\mathrm{x}}(1.5) = 9.167 = {\int }_0^{1}5.013 \mathrm{x} - \frac{5.013}{2} {\mathrm{x}}^2 + {\mathrm{m}}_{\mathrm{x},0} = {\left[\frac{5.013}{2} {\mathrm{x}}^2 - \frac{5.013}{6} {\mathrm{x}}^3 + {\mathrm{m}}_{\mathrm{x},0}\mathrm{x}\right]}_0^1 = 1.671 + {\mathrm{m}}_{\mathrm{x},0}$$

  $${\mathrm{m}}_{\mathrm{x},0} = {\mathrm{m}}_{\mathrm{x}}(1{)}^{+} = 9.167 - 1.671 = 7.496$$

  $${\mathrm{m}}_{\mathrm{x}}\left(1\right) = \frac{{\mathrm{m}}_{\mathrm{x}}(1{)}^{-} + {\mathrm{m}}_{\mathrm{x}}(1{)}^{+}}{2} = \frac{7.511 + 7.496}{2} = 7.503$$

  Secondo elemento utilizzando la teoria della flessione secondo Kirchhoff

4 Distribuzione livellata delle forze interne vx e mx secondo Kirchhoff

Nel processo di smussamento, i passaggi sopra descritti vengono eseguiti gradualmente nel programma. I valori smussati possono essere visualizzati graficamente con l'opzione di visualizzazione "Continuo nelle superfici".

Knowledge Base

KB 001606 | Livellamento delle forze interne di superficie in RFEM