Im Programm bestehen verschiedene Möglichkeiten für die Anzeige der ungeglätteten oder geglätteten Ergebnisse. Sie sind im RFEM-Handbuch beschrieben. Auch in einem früheren Fachbeitrag sind Glättungsvarianten zur Auswertung von Flächenschnittgrößen und -spannungen vorgestellt. Folgender Beitrag erläutert anhand eines Beispiels, wie die FE-Schnittgrößen bei der Glättung für die Werteermittlung herangezogen werden. Bei diesem Prozess spielt neben der Position eines finiten Elements auch die Plattentheorie - Mindlin oder Kirchhoff - eine Rolle.
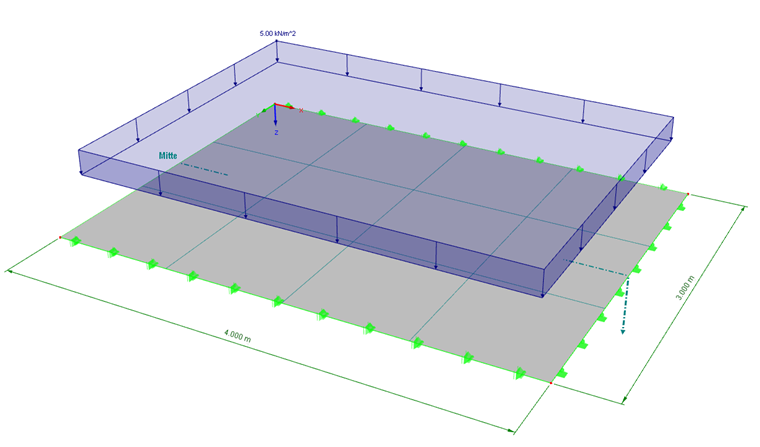
Beispiel: Platte nach Mindlin und Kirchhoff
Eine Platte mit den Abmessungen 4 m ⋅ 3 m wird als zweidimensionales Modell erzeugt. Die Platte ist beidseits an den kürzeren Randlinien gelenkig gelagert. Die Verdrehung der längeren Randlinien ist durch eine Einspannung behindert. Um Querdehnungeffekte zu unterdrücken, wird die Querdehnungszahl des Materials zu null gesetzt. Für einen Vergleich der Schnittgrößenermittlung nach den Plattenbiegetheorien von Kirchhoff und Mindlin wird eine Plattendicke von 80 cm gewählt. Damit ist ein Verhältnis d/L = 0.2 im Grenzbereich zwischen den beiden Biegetheorien gegeben (siehe https://www.dlubal.com/de/support-und-schulungen/support/faq/003158).
Die Maschenweite des FE-Netzes wird der Einfachheit halber mit 1 m festgelegt. Somit liegen 4 ⋅ 3 finite Elemente vor.
Auf die Platte wirkt eine Last von p = 5 kN/m². Das Eigengewicht wird im Lastfall nicht angesetzt.
Nicht geglättete Schnittgrößen
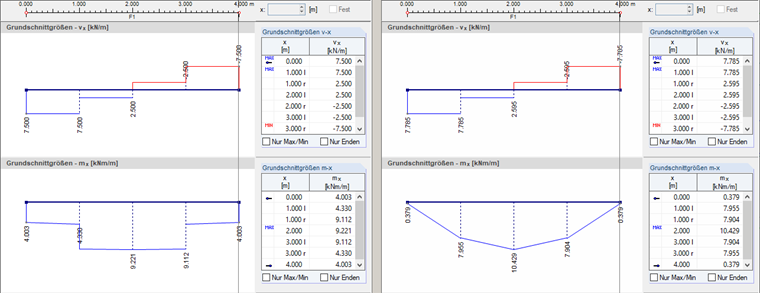
Die Ergebnisse des Rechenkerns für die Schnittgrößen vx und mx werden für einen Längsschnitt betrachtet, der in der Mitte der Platte verläuft. Der Verlauf der elementweisen, nicht geglätteten Schnittgrößen kann mit der Anzeigeoption "Nicht durchlaufend" dargestellt werden. Nach den Biegetheorien von Mindlin und Kirchhoff liegen die im Bild 02 gezeigten Verläufe vor.
Standardglättung für innenliegende Knoten
Für FE-Knoten, die innerhalb einer Fläche liegen, wird zunächst das arithmetische Mittel aus den Knotenwerten der benachbarten finiten Elemente gebildet. Für diesen Ansatz müssen die Elemente in einer Fläche und auf der gleichen Seite einer möglichen internen Linie liegen. Der Knoten darf kein benutzerdefinierter Knoten in der Fläche sein.
Für die Unstetigkeitsstelle bei x = 1.00 m sind dies intern folgende Werte (das Ergebnis dieses Schritts ist für die Ausgabe nicht verfügbar).
Mindlin:
Kirchhoff:
Glättung für Randknoten
An den Rändern einer Fläche (Glättungsoption "Durchlaufend innerhalb einer Fläche") oder eines Modells ("Durchlaufend gesamt") liegen keine benachbarten finiten Elemente vor, die für eine Mittelung der Knotenwerte dienen könnten. Daher wird ein anderer Ansatz gewählt, der in zwei Schritten erfolgt.
Im ersten Schritt werden die gemittelten Werte für diejenigen Knoten berechnet, die sich nicht am Rande einer Fläche oder des Modells befinden. Die Werte der Knoten an den Rändern werden so berechnet, dass die ursprünglichen Werte in den Mitten der finiten Elemente erhalten bleiben. Im zweiten Schritt werden dann die gemittelten Werte für die Randknoten bestimmt.
Für den Randknoten bei x = 0.00 m ergeben sich folgende Werte.
Mindlin:
Kirchhoff:
Querkräfte
Nach Mindlin werden die Querkräfte als erste Ableitung der Durchbiegung berechnet.
Diese Werte werden vom Rechenkern bestimmt und direkt verwendet. Die Glättung der Querkräfte erfolgt dann wie oben beschrieben je nach Lage des FE-Knotens in der Fläche.
Bei der Biegetheorie nach Kirchhoff werden die Querkräfte als dritte Ableitung der Durchbiegung berechnet.
Diese Werteermittlung über die dritte Ableitung ist mit einem erheblichen Genauigkeitsverlust verbunden. Aus diesem Grund werden die Querkräfte des Rechenkerns nicht verwendet, sondern durch einen verbesserten Ansatz aus den Ableitungen der Momente bestimmt.
Die in den Gleichungen dargestellten Momente mx, my und mxy repräsentieren die geglätteten Werte, die nach den oben beschriebenen Verfahren bestimmt werden. Damit ergeben sich genauere Werte für die Querkräfte als vonseiten des Rechenkerns.
Momente
Während die Momentenwerte in den Integrationspunkten den theoretischen Werten entsprechen, so führt die Extrapolation bei der Glättung über eine hyperbolische Paraboloidfunktion zu einem Verlust an Genauigkeit. Ein hyperbolisches Paraboloid drückt die Momentenverteilung im Element nur angenähert aus. Aus diesem Grund kommt ein verbesserter Algorithmus zur Anwendung, der die Extrapolation durch eine weiterentwickelte Querkraft-Integralmethode ersetzt. Da die Querkraftverteilung im Flächenelement der Form eines hyperbolischen Paraboloids entsprechend angenommen wird (Fläche zweiter Ordnung), stellt das Integral dieser Fläche eine Fläche dritter Ordnung dar, die den Momentenverlauf mit einer größeren Genauigkeit abbildet.
Dieser Ansatz korrespondiert mit den oben genannten Gleichungen zur Ermittlung der Querkräfte über die Ableitungen der Momente. Die Momente werden dann mit folgenden Gleichungen bestimmt.
Die Integrationskonstanten mx,0 und my,0 werden aus den Bedingungen des Wertes in Elementmitte berechnet.
S stellt die Fläche des Elements dar.
Die Werte der Schnittgrößen werden nach den oben beschriebenen Verfahren bestimmt, die Integrale durch eine numerische Integration. Die so ermittelten Momente werden dann nach dem Verfahren für innenliegende Knoten oder Randknoten geglättet.
Bei der Biegetheorie nach Mindlin ergeben sich im Beispiel folgende Werte.
Erstes Element:
Zweites Element:
Bei der Biegetheorie nach Kirchhoff ergeben sich folgende Werte.
Erstes Element:
Zweites Element:
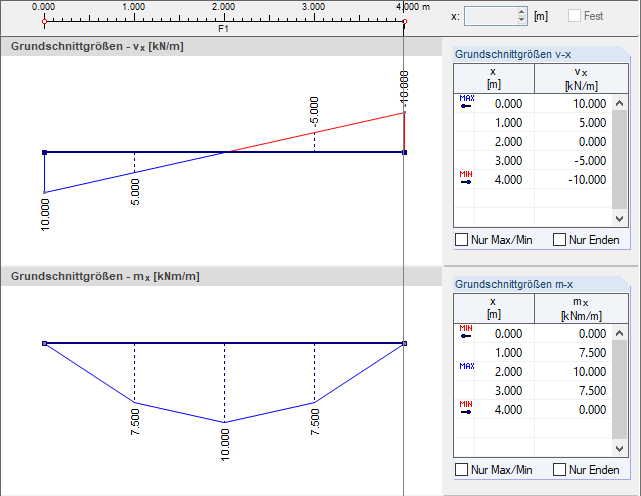
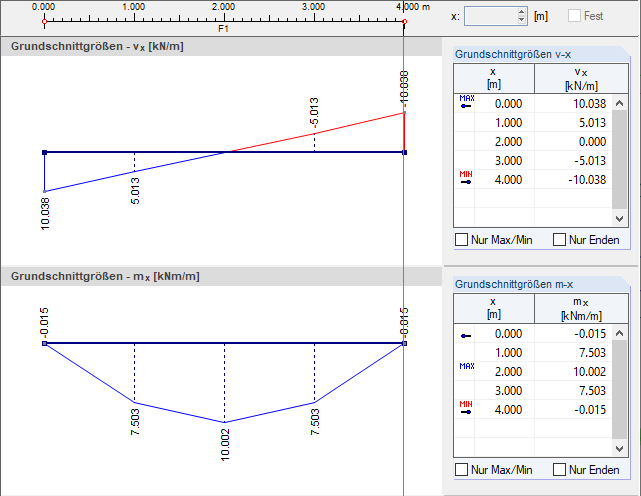
Beim Glättungsprozess laufen die oben beschriebenen Schritte sukzessive im Programm ab. Die geglätteten Werte lassen sich grafisch mit der Anzeigeoption "Durchlaufend innerhalb Flächen" darstellen.
.png?mw=350&hash=b023d6c658e181cb7d69028c0f3994dedab96fc5)
.jpg?mw=350&hash=bd355674e865e37d5548c329b8f5f0153cefe276)
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)