Les matériaux sont nécessaires pour la définition des surfaces, des sections et des corps volumiques. Les propriétés des matériaux influent sur la rigidité de ces objets.
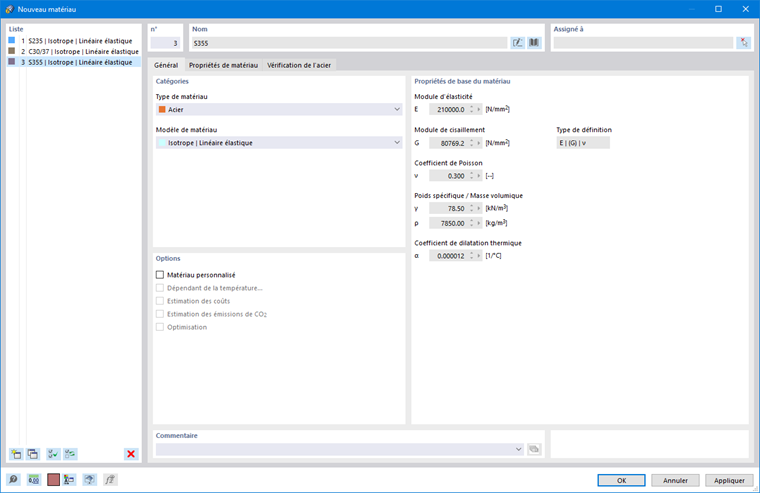
Nom
Vous pouvez attribuer un nom quelconque au matériau. Si la désignation correspond à une entrée de la bibliothèque, RFEM lit les propriétés de matériau enregistrées. Pour sélectionner le matériau dans la bibliothèque, cliquez sur le bouton
à la fin de la ligne de saisie. L'importation de matériaux est décrite dans le chapitre Bibliothèque de matériaux.
Pour les matériaux provenant de la bibliothèque, les 'Valeurs de matériau fondamentales' sont prédéfinies et non modifiables. Si vous souhaitez utiliser des valeurs définies par l'utilisateur pour le matériau, cochez la case de contrôle Matériau personnalisé dans la section 'Options' (voir section Matériau personnalisé).
Base
L'onglet Base gère les paramètres fondamentaux des matériaux. Il propose également des outils de gestion pour des propriétés spéciales que vous pouvez définir dans les onglets supplémentaires.
Catégories
Dans cette section, vous définissez le type de matériau et le modèle de matériau.
Type de matériau
Le type de matériau détermine quels paramètres et coefficients sont pertinents pour la conception. Cette classification prescrit également les coefficients de sécurité partiels du matériau, qui sont pris en compte selon les normes lors de la conception.
Pour un matériau de la bibliothèque, l'un des types de matériaux suivants est prédéfini.
Modèle de matériau
Les modèles de matériaux suivants sont disponibles dans la liste de sélection :
Isotrope | Linéaire élastique
Les propriétés de rigidité linéaires élastiques du matériau sont indépendantes de la direction. Elles peuvent être décrites comme suit :
|
E |
Module d’élasticité |
|
G |
Module de cisaillement |
|
ν |
Coefficient de Poisson |
Les conditions suivantes s'appliquent :
- E > 0
- G > 0
- -1 < ν ≤ 0,5 (pour les surfaces et les volumes ; pour les barres, illimité vers le haut)
La matrice de souplesse (inverse de la matrice de rigidité) pour les surfaces est :
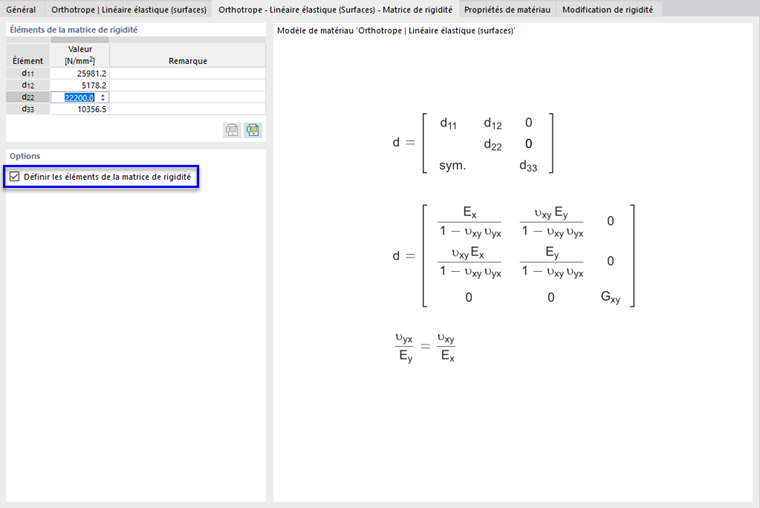
Orthotrope | Linéaire élastique (Surfaces)
Ce modèle de matériau permet de définir des propriétés de rigidité qui diffèrent dans les deux directions de la surface x et y. Cela permet, par exemple, de représenter les propriétés des plastiques renforcés de fibres de verre, des plaques nervurées ou les directions d'armature des dalles. Les axes de surface x et y sont perpendiculaires l'un à l'autre dans le plan de la surface.
Pour définir différentes propriétés de matériau pour les directions x et y, activez la case de contrôle 'Matériau personnalisé' dans la section 'Options'. Dans l'onglet 'Orthotrope - Linéaire élastique (Surfaces)', vous pouvez alors définir les paramètres du matériau.
Pour avoir une matrice de rigidité définie positive, les conditions suivantes doivent être remplies :
- Ex > 0 ; Ey > 0
- Gyz > 0 ; Gxz > 0 ; Gxy > 0
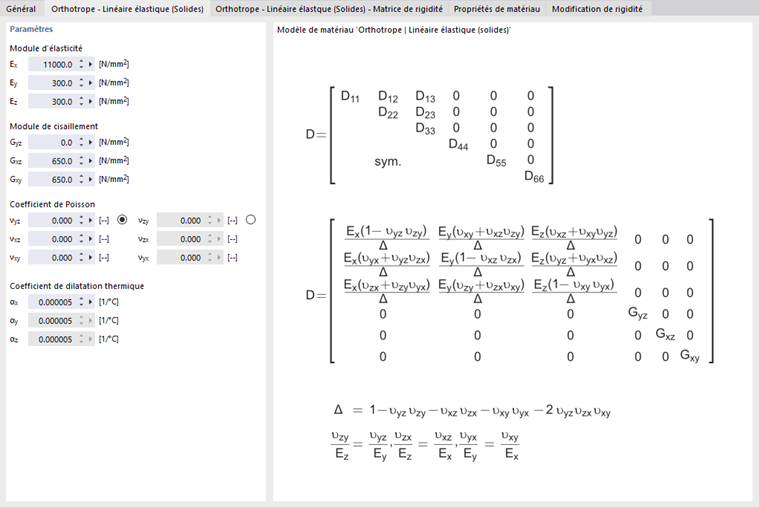
Orthotrope | Linéaire élastique (Volumes)
Dans le modèle de matériau orthotrope tridimensionnel, les rigidités élastiques peuvent être définies séparément dans toutes les directions du volume. Pour définir des propriétés de matériau différentes pour chaque direction, activez la case de contrôle 'Matériau personnalisé' dans la section 'Options'. Dans l'onglet 'Orthotrope - Linéaire élastique (Volumes)', vous pouvez alors définir les paramètres du matériau.
Les éléments de la matrice de rigidité dérivés des saisies seront indiqués dans l'onglet 'Orthotrope - Linéaire élastique (Volumes) - Matrice de rigidité'.
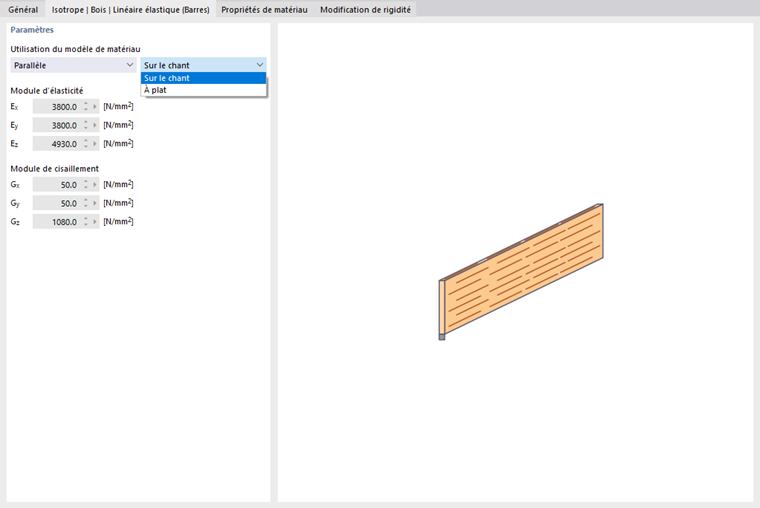
Isotrope | Bois | Linéaire élastique (Barres)
Ce modèle de matériau est disponible pour les matériaux de type 'Bois'. Il permet, par exemple, de représenter les propriétés d'une plaque OSB dans un modèle de barre, capturant les rigidités différentes selon la position d'installation. Vous pouvez définir la position de la plaque dans l'onglet 'Isotrope Bois | Linéaire élastique (Barres)' via les deux listes.
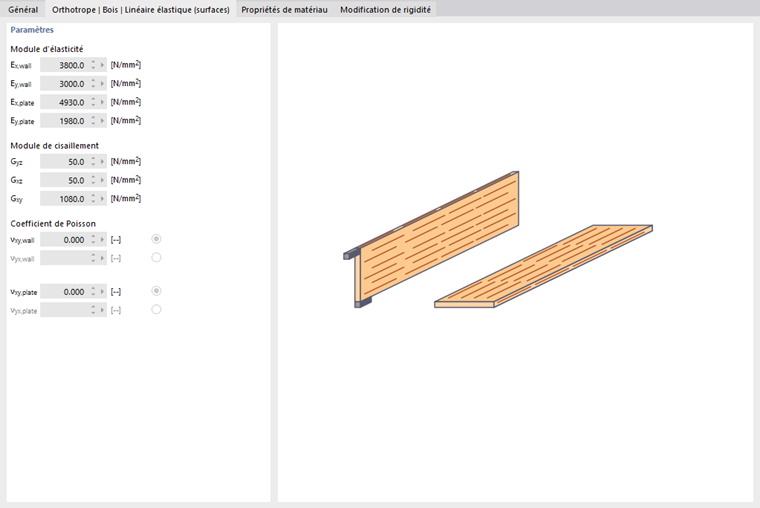
Orthotrope | Bois | Linéaire élastique (Surfaces)
Pour les matériaux de type 'Bois', ce modèle de matériau permet de contrôler le module d'élasticité par rapport à l'effet porteur en tant que mur ou dalle, ainsi que le module de cisaillement Gxy : les plaques OSB, par exemple, présentent des rigidités directionnelles selon leur position dans le modèle.
Les paramètres de rigidité peuvent être définis dans l'onglet 'Orthotropique Bois | Linéaire élastique (Surfaces)'. Pour les matériaux en bois de la bibliothèque, des valeurs standard sont préréglées. Pour définir différentes propriétés de matériau pour chaque direction, activez d'abord la case de contrôle 'Matériau personnalisé' dans la section 'Options'.
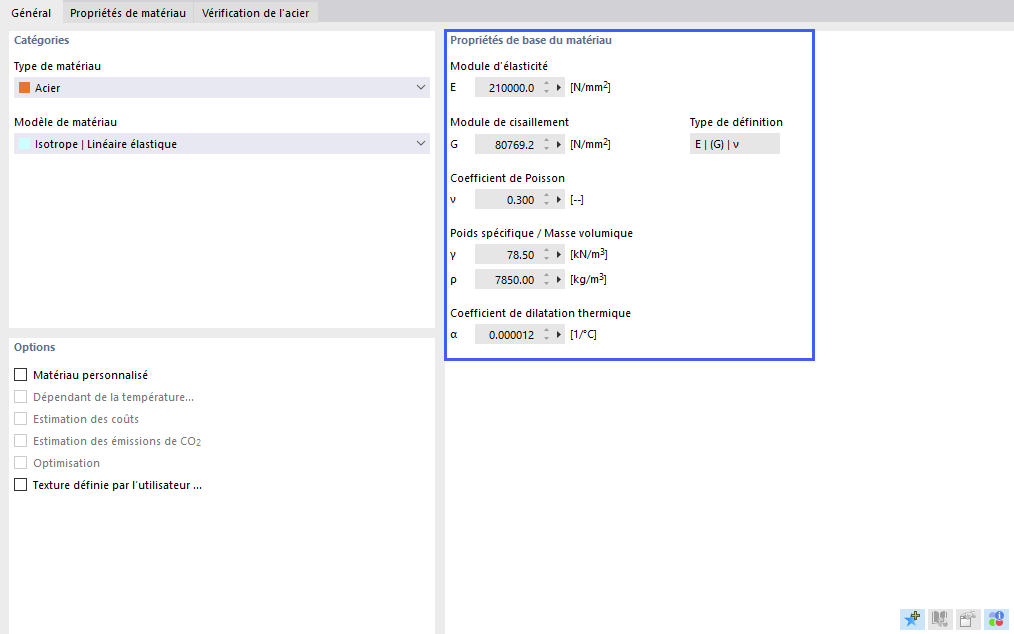
Valeurs de matériau fondamentales
Cette section de l'onglet 'Base' indique les principales valeurs caractéristiques du matériau.
Module d'élasticité
Le module d'élasticité E décrit le rapport entre la contrainte normale et la déformation.
Module de cisaillement
Le module de cisaillement G, également appelé module de glissement, est une deuxième caractéristique pour décrire le comportement élastique d'un matériau linéaire, isotrope et homogène. La déformation est dans ce cas basée sur une contrainte de cisaillement.
Coefficient de Poisson
Le coefficient de Poisson ν, également appelé nombre de Poisson, est requis pour déterminer la contraction transversale. Pour les matériaux isotropes, le coefficient de Poisson est généralement compris entre 0,0 et 0,5. À partir d'une valeur de 0,5 (par exemple, le caoutchouc), il est donc à supposer qu'il ne s'agit pas d'un matériau isotrope.
La relation entre le module d'élasticité, le module de cisaillement et le coefficient de Poisson pour un matériau isotrope est décrite dans l'équation Coefficient de Poisson.
Si vous saisissez un Matériau personnalisé avec ses propriétés isotropes, RFEM déterminera le coefficient de Poisson à partir des valeurs du module E et G. Vous pouvez, si nécessaire, modifier ce paramètre par défaut dans la liste 'Type de définition'.
Type de définition
| E | G | (ν) | Le coefficient de Poisson est déterminé à partir des modules E et G |
| E | (G) | ν | Le module de cisaillement est déterminé à partir du module E et du coefficient de Poisson |
| E | G | ν | Les modules E, G et le coefficient de Poisson sont indépendants les uns des autres |
Poids spécifique / Densité
Le poids spécifique γ décrit le poids du matériau par unité de volume. Cette option est particulièrement importante pour le cas de charge "Poids propre" : la charge propre automatique du modèle est déterminée à partir du poids spécifique et des sections transversales des barres utilisées ou des surfaces et volumes.
La densité ρ décrit la masse du matériau par unité de volume. Cette information est requise pour les études dynamiques.
Coefficient de dilatation thermique
Le coefficient de dilatation thermique α décrit la relation linéaire entre les variations de température et de longueur (dilatation du matériau lors du chauffage, contraction lors du refroidissement).
Le coefficient de dilatation thermique est pertinent pour les types de charge 'Température' et 'Variation de température'.
Dans l'onglet Valeurs de matériau ou via le bouton image
Matériau personnalisé
Pour les matériaux de la bibliothèque, les valeurs des matériaux sont prédéfinies. Elles ne peuvent donc pas être modifiées directement dans les champs de saisie. Pour ajuster les propriétés d'un matériau, activez la case à cocher 'Matériau personnalisé'. Cela rend les champs de saisie des principales valeurs de matériau dans l'onglet 'Base' accessibles. Vous pouvez également modifier les valeurs caractéristiques spécifiques à la conception dans l'onglet 'Valeurs de matériau' (voir image Adapter les valeurs de matériau). Dans l'onglet 'Modification de la rigidité', il est possible de mettre à l'échelle le module E et le module G globalement avec un facteur (voir image Ajuster la rigidité du matériau).
Dépendant de la température
Pour définir un matériau linéaire élastique avec des propriétés contrainte-déformation dépendantes de la température, activez les cases à cocher 'Personnalisé' et 'Dépendant de la température'. Vous pouvez alors définir les valeurs de matériau dépendantes de la température dans l'onglet Dépendant de la température.
Valeurs de matériau
Dans l'onglet Valeurs de matériau, toutes les valeurs caractéristiques du matériau pertinentes pour l'analyse structurelle et la conception dans les add-ons sont indiquées.
Modification de la rigidité
L'onglet Modification de la rigidité est affiché lorsque vous avez coché l'option Matériau personnalisé dans l'onglet 'Base'. Vous pouvez ici ajuster globalement la rigidité du matériau, par exemple pour tenir compte des facteurs de sécurité ou des propriétés de matériau atténuées.
Dans la liste de la section 'Type de modification', deux possibilités sont disponibles :
- Facteur de division pour les modules E et G
- Facteur de multiplication pour les modules E et G
Indiquez dans la section 'Paramètres' le facteur avec lequel vous souhaitez ajuster la rigidité du matériau.
Pour un matériau avec des propriétés orthotropes, vous pouvez ajuster dans l'onglet Orthotrope | Linéaire élastique les modules E et G ainsi que les coefficients de Poisson (voir image Matrice de rigidité). Si vous activez l'option 'Définir les éléments de la matrice de rigidité' dans l'onglet Orthotrope | Linéaire élastique | Matrice de rigidité, vous pouvez également définir manuellement les éléments de la matrice de rigidité.
Dépendant de la température
L'onglet Dépendant de la température est affiché lorsque vous avez coché les options Matériau personnalisé et Dépendant de la température dans l'onglet 'Base'. Vous pouvez ici décrire les valeurs caractéristiques du matériau dépendantes de la température. Les propriétés matérielles dépendantes de la température sont prises en compte pour les objets soumis à des contraintes thermiques par température ou variation de température. Lors du calcul des charges thermiques, la température finale de l'étape respective est appliquée.
Sélectionnez dans la liste 'Valeur caractéristique dépendante de la température' une propriété de matériau, par exemple le module E. Générez ensuite avec le bouton
les lignes de tableau nécessaires pour saisir les températures avec les valeurs associées ligne par ligne. Avec le bouton
, vous pouvez également importer les données à partir d'un tableau Excel.
La 'Température de référence' détermine les rigidités pour les objets ne présentant pas de charges thermiques. Avec une valeur de référence de, par exemple, 300 °C, le module E réduit de ce point de la courbe de température est appliqué pour toutes les barres et surfaces.
Bibliothèque de matériaux personnalisés
Vous pouvez enregistrer un matériau personnalisé dans une bibliothèque en tant que modèle. Ainsi, vous n'avez pas besoin de définir à nouveau les propriétés du matériau dans d'autres projets.
Enregistrer le matériau
Pour enregistrer le matériau actuel en tant que matériau personnalisé, cliquez après avoir défini les valeurs caractéristiques du matériau sur le bouton
au bas de la section 'Valeurs de matériau fondamentales'.
La boîte de dialogue 'Nouveau matériau personnalisé' apparaît.
Entrez dans le champ 'Nom' la désignation du matériau. Le cas échéant, vous pouvez encore ajuster les valeurs caractéristiques du matériau. Cliquez sur OK pour enregistrer ensuite le matériau personnalisé dans la bibliothèque.
Importer le matériau
Pour importer un matériau personnalisé à partir de la bibliothèque, cliquez dans la section 'Valeurs de matériau fondamentales' sur le bouton
.
La boîte de dialogue 'Modifier le matériau personnalisé' apparaît. Dans cette bibliothèque avec vos matériaux enregistrés (voir image Dialogue 'Nouveau matériau personnalisé'), vous pouvez sélectionner l'entrée correspondante et l'adopter ensuite avec OK.
Si vous avez importé un matériau personnalisé et souhaitez modifier les propriétés de manière générale, vous pouvez ajuster les valeurs caractéristiques du matériau via le bouton
(dans la section 'Valeurs de matériau fondamentales') dans la bibliothèque.
Définir l'emplacement de la bibliothèque
La bibliothèque avec les matériaux personnalisés est par défaut enregistrée dans le fichier user_library_material.dbm dans le répertoire des configurations utilisateur. Vous pouvez vérifier ce répertoire dans les Options du programme.
Sélectionnez dans la catégorie Base de données l'entrée Bibliothèque de matériaux utilisateur (1). Ensuite, affichez le dossier du fichier user_library_material.dbm via le bouton
(2). Si vous souhaitez utiliser une autre bibliothèque de matériaux située sur un lecteur réseau de votre entreprise, définissez le répertoire du fichier et cliquez sur 'Enregistrer'. Vous pouvez également transférer votre fichier sur un autre ordinateur et y définir le chemin d'accès dans le même dialogue.