Описание работы
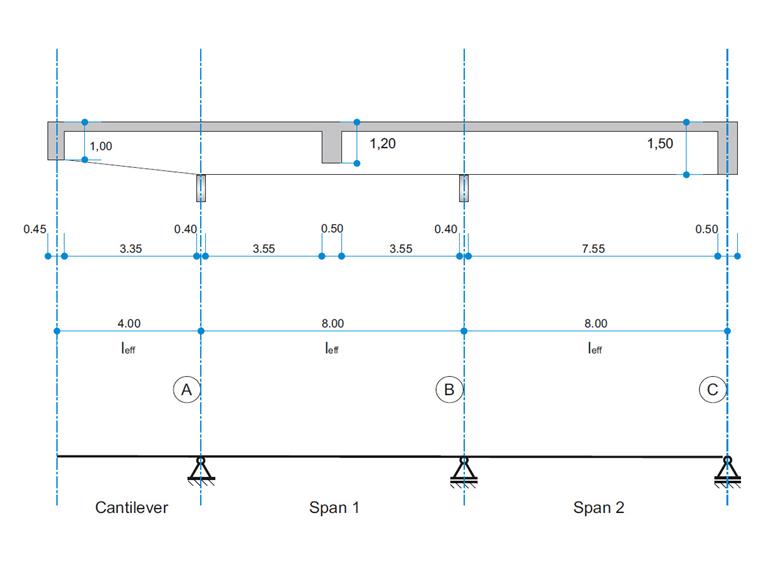
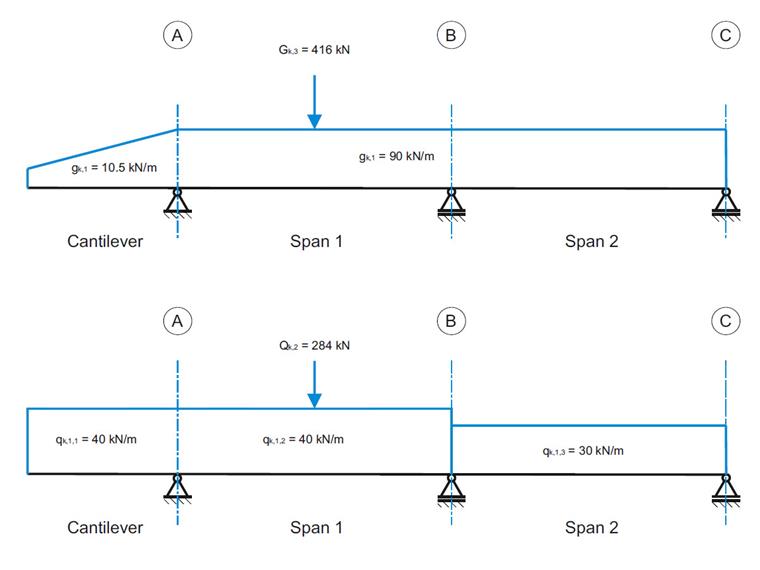
Железобетонная балка представляет собой двухпролетную балку с консолью. Сечение меняется по длине консоли (коническое сечение). Внутренние силы, требуемая продольная и поперечная арматура для предельного состояния по несущей способности, рассчитываются и сравниваются с результатами в {%ref#Refer [1]]].
Параметры RFEM
- Учет частичного перераспределения опорного момента по до 5,5
- Снижение моментов или подбор сечений по моментам на лицевой стороне монолитной опоры по по 5.3.2.2
- Редукция поперечных сил в области опоры и расстояние d по по 6.2.1(8)
- Тип распределения используемого сечения - коническое в начале стержня, чтобы учесть изменение высоты сечения.
Результаты
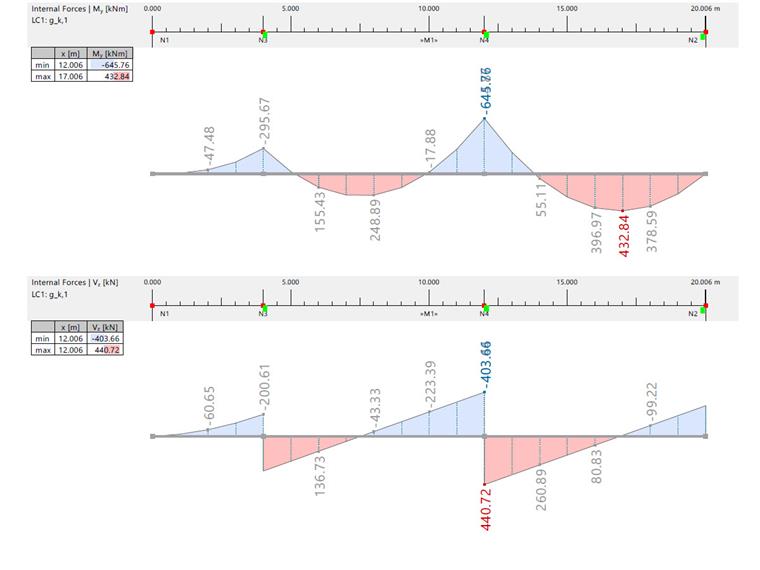
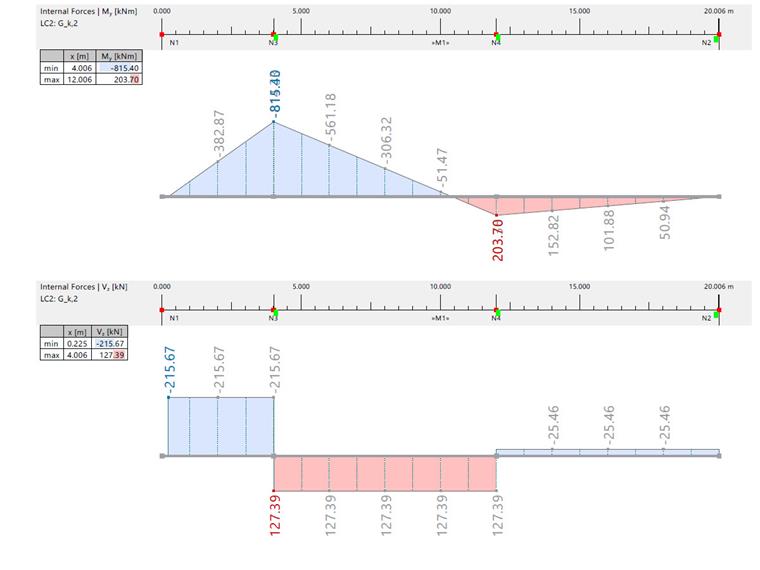
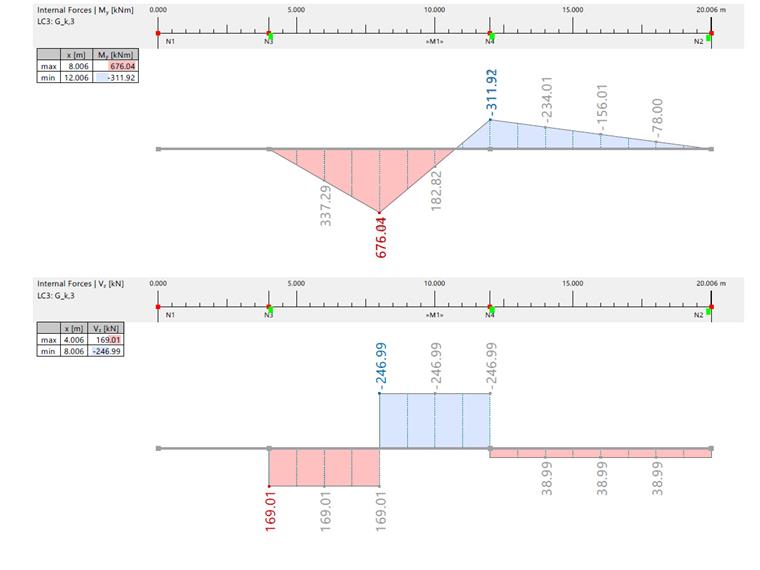
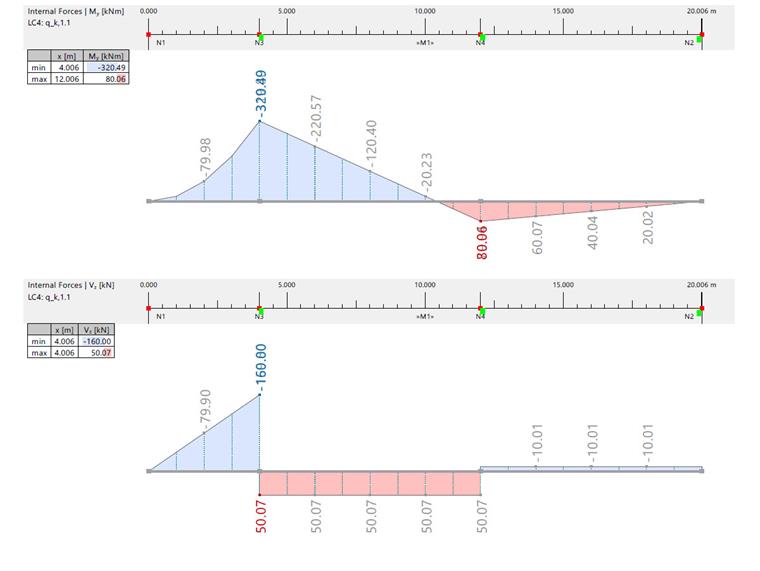
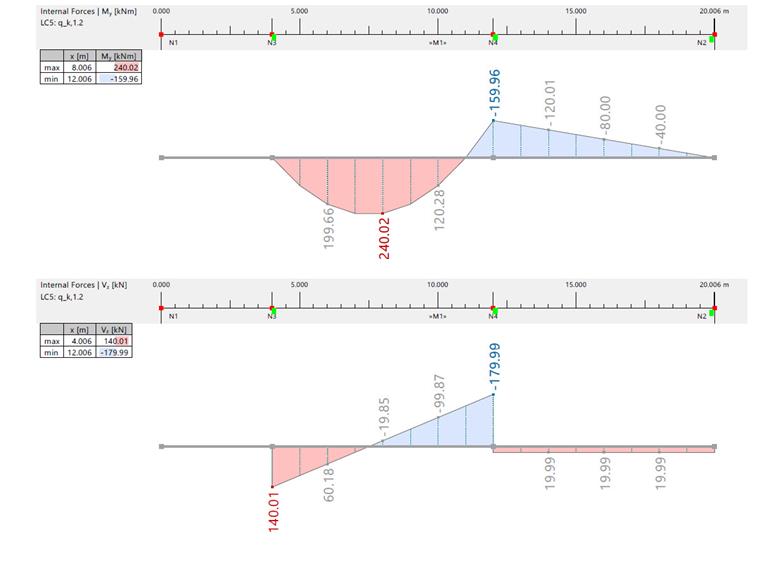
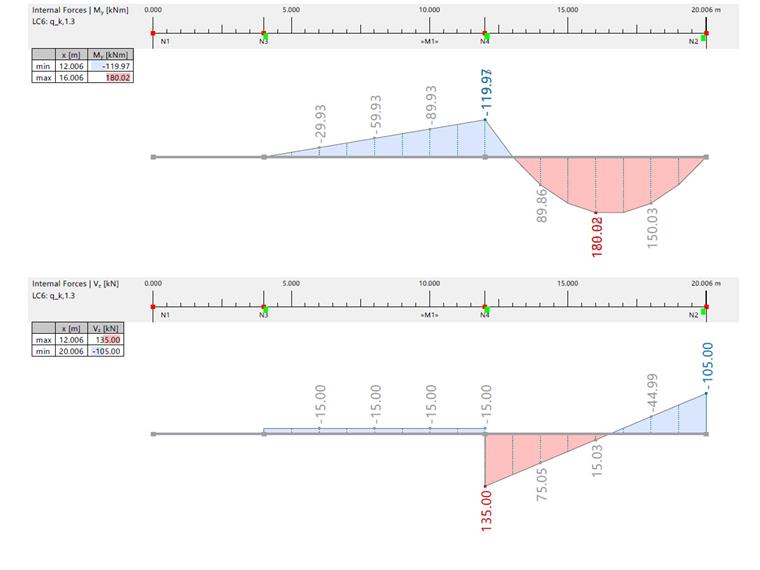
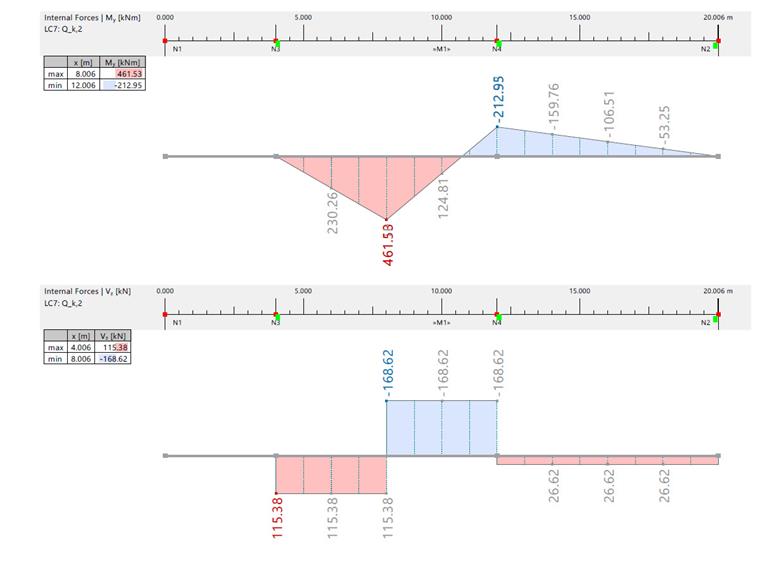
Изгибающий момент и поперечная сила от постоянных и временных нагрузок
| Изгибающий момент и поперечная сила от gk,1
|
| Внутренняя сила
|
Единица измерения
|
RFEM/Аналитическое решение
|
Пролёт 1
|
Пролёт 2
|
Ось A
|
Ось B
|
Ось C
|
| изгибающий момент
|
[кНм]
|
RFEM
|
248,890
|
432,840
|
-296,460
|
-645,760
|
0
|
| Аналитическое решение
|
249,000
|
433.000
|
-296.000
|
-646.000
|
0
|
| поперечная сила
|
[кН]
|
RFEM
|
-43.330
|
80,830
|
-201.000/316.340
|
-403.660/440.720
|
-279,280
|
| Аналитическое решение
|
-44.000
|
81.000
|
-201.000/316.000
|
-404.000/441.000
|
-279.000
|
<br/>
</p>
==== Внутренние силы ====
Следующая таблица содержит все сочетания нагрузок для предельного состояния по несущей способности:
| Сочетание нагрузок
|
Приданные к загружениям
|
| СН1
|
1,00·ЗГ1 + 1,00·ЗГ2 + 1,00·ЗГ3
|
| СН2
|
1,35·ЗГ1 + 1,35·ЗГ2 + 1,35·ЗГ3 + 1,50·ЗГ4 + 1,50·ЗГ5 + 1,50·ЗГ6 + (1,50·0,80)·ЗГ7
|
| СН3
|
1,35·ЗГ1 + 1,35·ЗГ2 + 1,35·ЗГ3 + (1,50·0,70)·ЗГ4 + (1,50·0,70)·ЗГ5 + (1,50·0,70)·ЗГ6 + 1,50·ЗГ7
|
| СН4
|
1,35·ЗГ1 + 1,00·ЗГ2 + 1,35·ЗГ3 + 1,50·ЗГ5 + 1,50·ЗГ6 + (1,50·0,80)·ЗГ7
|
| СН5
|
1,35·ЗГ1 + 1,00·ЗГ2 + 1,35·ЗГ3 + (1,50·0,70)·ЗГ5 + 1,50·ЗГ7
|
| СН6
|
1,00·ЗГ1 + 1,35·ЗГ2 + 1,35·ЗГ3 + (1,50·0,70)·ЗГ4 + 1,50·ЗГ7
|
| СН7
|
1,35·ЗГ1 + 1,00·ЗГ2 + 1,35·ЗГ3 + (1,50·0,70)·ЗГ5 + (1,50·0,70)·ЗГ6+ 1,50·ЗГ7
|
| СН8
|
1,35·ЗГ1 + 1,35·ЗГ2 + 1,00·ЗГ3 + 1,50·ЗГ4 + 1,50·ЗГ6
|
| СН9
|
1,35·ЗГ1 + 1,35·ЗГ2 + 1,35·ЗГ3 + 1,50·ЗГ4 + 1,50·ЗГ5 + (1,50·0,80)·ЗГ7
|
<br />
</p>
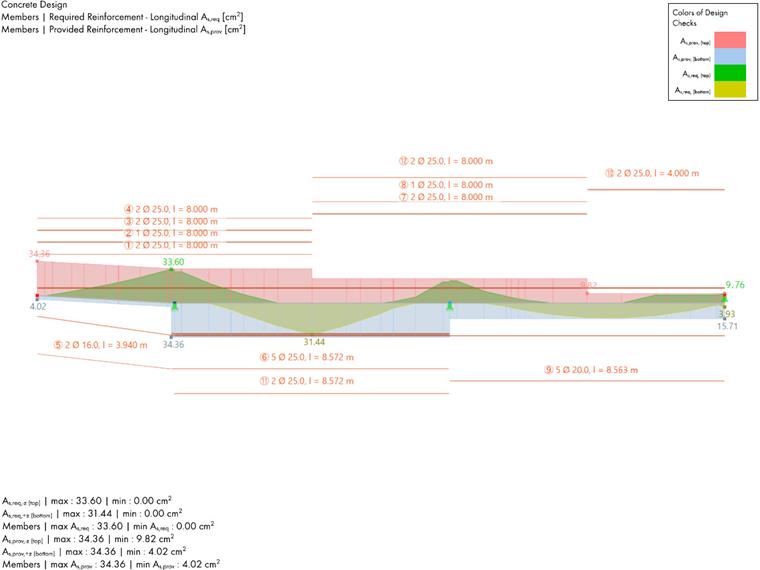
==== Требуемая продольная арматура ====
В литературе указано, что в сочетаниях нагрузок 4 учитывалось 15%-ное перераспределение момента на опоре B, а 12%-ное перераспределение момента - в сочетании нагрузок 7. Программа RFEM, напротив, применяет одинаковое перераспределение момента для всех сочетаний нагрузок. Чтобы облегчить значимое сравнение с литературой, в модель RFEM будут внесены коррективы. Затем будет представлено фактическое решение, найденное программой RFEM.
'''Сравнение результатов RFEM с результатами из литературы:'''
'''Опора A:'''
Балка монолитно соединена с опорой, и поэтому находится на грани опоры. Тем не менее, в литературе при расчете момента на грани опоры не учитывается влияние нагрузки. Однако, для значимого сравнения с результатами в RFEM, необходимо выполнить перерасчет с учетом влияния нагрузки. Расчетный момент на грани опоры без учета влияния нагрузки M
Ed составляет
-1819,0 кНм. С учетом действия нагрузок M
Ed увеличивается до
-1823,0 кНм.
|
RFEM
|
Аналитическое решение
|
Отношение
|
| Загружение
|
Расчётный изгибающий момент MEd
|
Требуемая арматура As,stat,tot
|
Расчётный изгибающий момент MEd
|
Требуемая арматура As,stat,tot
|
MED
|
As,stat,tot
|
|
[кНм]
|
[см2 ]
|
[кНм]
|
[см2 ]
|
[кНм]
|
[см2 ]
|
| СН8
|
-1824.790
|
32,50
|
-1823.000
|
31,60
|
1,00
|
1,02
|
<br />In the literature, it is assumed that the cross-section height at the edge of the support is equal to the cross-section height at the middle of the support. Тем не менее, в программе RFEM из-за конического сечения учитывается фактическая высота сечения. Как результат, это приводит к более высоким требованиям к арматуре в RFEM.
'''Опора B:'''
Критическим сочетанием нагрузок в данном случае является сочетание нагрузок 4. Согласно литературе, коэффициент перераспределения момента в опоре B задан равным 0,850.
<br />When calculating the design moment, the literature takes into consideration that the moment at the face of the support should not be less than 0.65 of the full fixed end moment (DIN EN 1992-1-1, 5.3.2.2). Данное условие в программе RFEM не реализовано. Это объясняет разницу в расчетном моменте.
'''Пролет 1:'''
Поскольку балка задана в RFEM как непрерывный стержень, невозможно задать эффективную ширину b
eff для каждого пролета. Для упрощения затем используется наименьшее значение из двух значений полезной ширины пролета 1 и 2. b
eff затем задано равным 2,620 м. В литературе учитывается 12% перераспределение момента для сочетания нагрузок 7, поэтому коэффициент перераспределения момента в средней опоре теперь равен 0,880.
| Пролёт 1
|
|
RFEM
|
Аналитическое решение
|
Отношение
|
| Загружение
|
Расчётный изгибающий момент MEd
|
Требуемая арматура As,stat,tot
|
Расчётный изгибающий момент MEd
|
Требуемая арматура As,stat,tot
|
MEd
|
As,stat,tot
|
|
[кНм]
|
[см2 ]
|
[кНм]
|
[см2 ]
|
[кНм]
|
[см2 ]
|
| СН7
|
1926,280
|
30,13
|
1927.000
|
33.10
|
0,99
|
0,91
|
<br />'''Span 2:'''<br />In this case, no moment redistribution is considered. Коэффициент перераспределения момента установлен на 1.000.
| Пролёт 2
|
|
RFEM
|
Аналитическое решение
|
Отношение
|
| Загружение
|
Расчётный изгибающий момент MEd
|
Требуемая арматура As,stat,tot
|
Расчётный изгибающий момент MEd
|
Требуемая арматура As,stat,tot
|
MEd
|
As,stat,tot
|
|
[кНм]
|
[см2 ]
|
[кНм]
|
[см2 ]
|
[кНм]
|
[см2 ]
|
| СН8
|
885,520
|
13,79
|
- 895,000
|
15.10
|
0,99
|
0,91
|
<br>In the literature, the required longitudinal reinforcement is determined using approximation methods for T-beams according to DAstb-heft 425. При использовании данного метода предполагается, что сжимающая сила в полке находится в центре полки (h
f/2). в программе RFEM требуемая арматура определяется на основе расчета сечений. Это приводит к тому, что требуемая арматура ниже, чем указано в литературе.
'''Решение, предоставленное программой RFEM,'''
Теперь перераспределение момента в средней опоре задано для всех сочетаний нагрузок на 15%. Результаты обобщены в таблицах ниже.
'''Опора A:'''
загружение 8 дает наибольший изгибающий момент и, следовательно, является решающим.
| Опора A
|
| Загружение
|
Расчётный изгибающий момент MEd
|
Требуемая арматура As,stat,tot
|
|
[кНм]
|
[см2 ]
|
| СН8
|
-1824.840
|
32,32
|
<br />'''Support B:'''<br />
<br />'''Span 1:'''<br /> When moment redistribution is taken into consideration in all load combinations, CO5 has the highest design bending moment in Span 1.<br />
<br /> '''Span 2:'''<br />CO8 has a design moment after moment redistibution M
Ed of 940 kNm.<br />
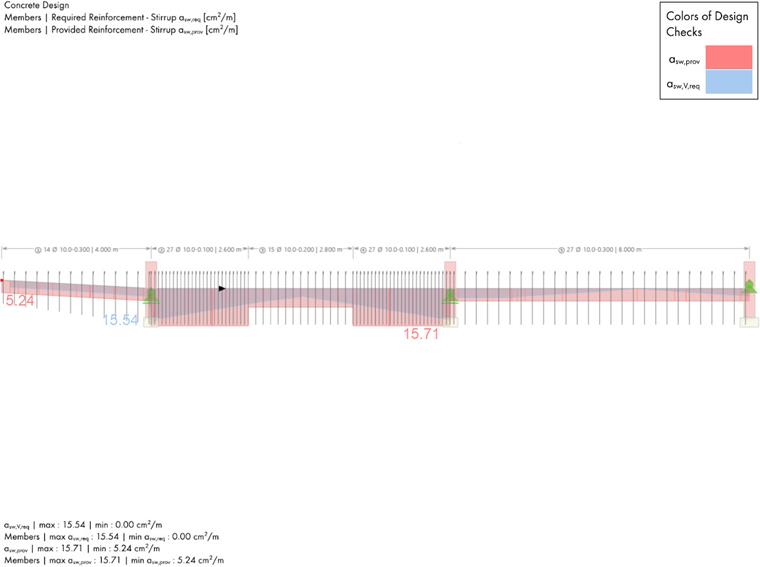
==== Арматура, работающая на сдвиг ====
'''Поперечная арматура в консоли:'''
Чтобы определить требуемое количество хомутов в консоли, нужно проверить в 3 местах. Результаты представлены в таблице ниже:
| консоль
|
| x-разрез
|
Параметр
|
Символ
|
Единица измерения
|
RFEM
|
Аналитическое решение
|
Отношение
|
| x = 0,45 м
|
Расчётная высота
|
d
|
[м]
|
0,940
|
0,920
|
1,02
|
| Внутреннее плечо
|
Z
|
[м]
|
0,848
|
0,828
|
1,02
|
| Поперечная сила
|
VEd
|
[кН]
|
-327.190
|
-328,000
|
0,99
|
| Расчётный изгибающий момент
|
MED
|
[кНм]
|
-73.320
|
-74.000
|
0,99
|
| Расчётная сдвиговая составляющая силы в сжатой зоне
|
Vccd
|
[кН]
|
12,550
|
13.000
|
0,99
|
| Расчётная поперечная сила
|
VEd,red
|
[кН]
|
314,640
|
314,000
|
1,0
|
| Несущая способность на сдвиг без армирования
|
vrd,cc
|
[кН]
|
219,420
|
221,00
|
0,99
|
| Угол наклона сжатой диагонали бетона
|
cot Θ
|
[-]
|
3,0
|
3,0
|
1,0
|
| Прочность сжатой диагонали
|
Vrd,max
|
[кН]
|
996,230
|
1003,000
|
0,99
|
| Требуемая арматура
|
asw,req
|
[см2/м]
|
2,84
|
2,91
|
0,98
|
| х = 1,37 м
|
Расчётная высота
|
d
|
[м]
|
1,070
|
1,050
|
1,02
|
| Внутреннее плечо
|
Z
|
[м]
|
0,965
|
0,945
|
1,02
|
| Поперечная сила
|
VEd
|
[кН]
|
-417.720
|
-418.000
|
1,00
|
| Расчётный изгибающий момент
|
MED
|
[кНм]
|
-414.250
|
-415.000
|
1,00
|
| Расчётная сдвиговая составляющая силы в сжатой зоне
|
Vccd
|
[кН]
|
62.210
|
66,000
|
0,94
|
| Расчётная поперечная сила
|
VEd,red
|
[кН]
|
355,510
|
353.000
|
1,01
|
| Несущая способность на сдвиг без армирования
|
vrd,cc
|
[кН]
|
250,070
|
252,000
|
0,99
|
| Угол наклона сжатой диагонали бетона
|
cot Θ
|
[-]
|
3,0
|
3,0
|
1,0
|
| Прочность сжатой диагонали
|
Vrd,max
|
[кН]
|
1135,860
|
1144.000
|
0,99
|
| Требуемая арматура
|
asw,req
|
[см2/м]
|
2,83
|
2,86
|
0,99
|
| х = 2,37 м
|
Расчётная высота
|
d
|
[м]
|
1,210
|
1,190
|
1,02
|
| Внутреннее плечо
|
Z
|
[м]
|
1,090
|
1,070
|
1,02
|
| Поперечная сила
|
VEd
|
[кН]
|
-541.800
|
-543.000
|
1,0
|
| Расчётный изгибающий момент
|
MED
|
[кНм]
|
-891.790
|
-893,00
|
1,00
|
| Расчётная сдвиговая составляющая силы в сжатой зоне
|
Vccd
|
[кН]
|
118,250
|
125,000
|
0,95
|
| Расчётная поперечная сила
|
VEd,red
|
[кН]
|
423.550
|
418,000
|
1,01
|
| Несущая способность на сдвиг без армирования
|
vrd,cc
|
[кН]
|
283,220
|
285,000
|
0,99
|
| Угол наклона сжатой диагонали бетона
|
cot Θ
|
[-]
|
3,0
|
3,0
|
1,0
|
| Прочность сжатой диагонали
|
Vrd,max
|
[кН]
|
1286,410
|
1298,000
|
0,99
|
| Требуемая арматура
|
asw,req
|
[см2/м]
|
2,98
|
2,99
|
1,0
|
<br>'''Span 1:''' <br /> The decisive member location for the calculation of the stirrups in field 1 is at a distance d from the right edge of the support A.<br />
<br>'''Span 2:'''<br>The calculation of the stirrups is done analog to span 1.<br />
<br>
Различия в результатах для пролета 2 связаны с тем, что в литературе учитывалась поперечная сила на опоре В после перераспределения момента. Однако перераспределение момента не влияет на расчет поперечной силы в RFEM.
..png?mw=320&hash=bd2e7071b02d74aef6228d22c4b83867d2d7e1a5)
_1.jpg?mw=350&hash=ab2086621f4e50c8c8fb8f3c211a22bc246e0552)
-querkraft-hertha-hurnaus.jpg?mw=350&hash=3306957537863c7a7dc17160e2ced5806b35a7fb)
-gigapixel-standard_v2-2x.jpg?mw=350&hash=9166b062b07ae89e60417bff40b33fe9043f9d5e){kind=tracking}
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
