VE 1025 | Vérification du béton armé d'une poutre continue à deux travées avec porte-à-faux

Description du projet

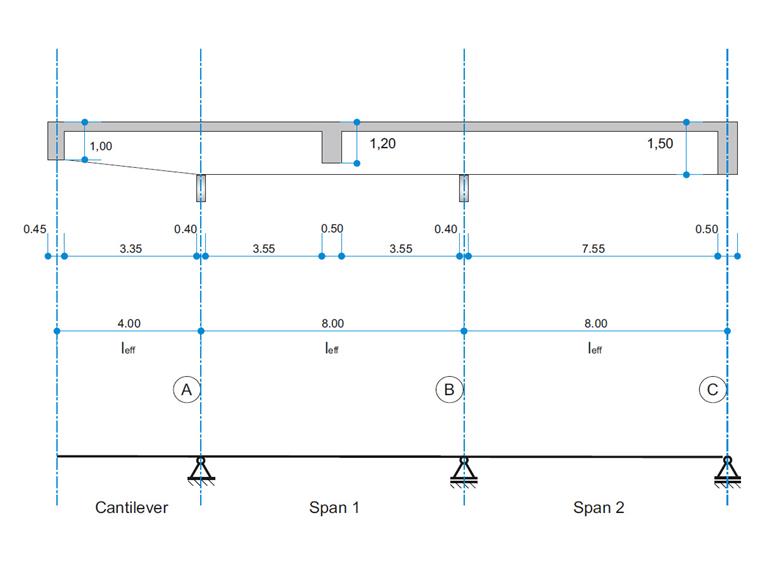
Une poutre en béton armé est calculée comme une poutre à deux travées avec un porte-à-faux. La section varie le long du porte-à-faux (section à inertie variable). Les efforts internes, les armatures longitudinales et de cisaillement requises pour l'état limite ultime sont calculés et comparés aux résultats dans [1].

Matériau	Béton C25/30	Module d'élasticité	E	31 000	N/mm2
		Valeur de calcul de la résistance du béton en compression	fcd	14,167	N/mm2
	Acier de béton armé B500S(B)	Limite caractéristique d'élasticité	fyk	500 000	N/mm2
		Limite d'élasticité de calcul	fyd	434,783	N/mm2
Géométrie	Structure	Longueur du porte-à-faux	leff,porte-à-faux	4 000	m
		Longueur de travée 1	leff,1	8 000	m
		Longueur de travée 2	leff,2	8 000	m
	Section	Hauteur	h	1 500	mm
		Largeur	b	2 620	mm
		Hauteur de semelle	hf	150	mm
		Largeur de l'âme	bw	380	mm
		Enrobage de béton	cnom	35	mm
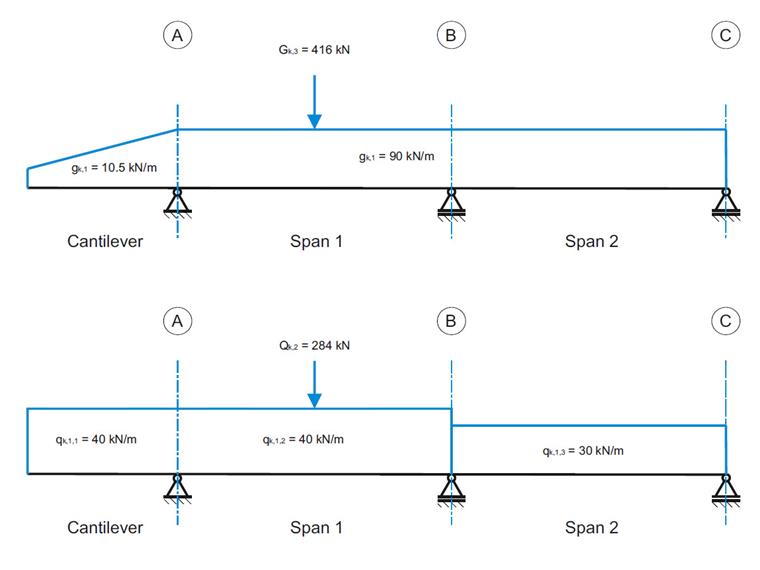
Charges	Charges permanentes	CC1	gk,1	10 500 - 90 000 (trapézoïdale)	kN/m
		CC2	Gk,2	216 000	kN
		CC3	Gk,3	416 000	kN
	Charges d'exploitation	CC4	qk,1,1	40 000	kN/m
		CC5	qk,1,2	40 000	kN/m
		CC6	qk,1,3	30 000	kN/m
		CC7	Qk,2	284,000	kN

Paramètres RFEM

• Considération de la redistribution limitée des moments d'appui selon 5.5
• Réduction des moments ou dimensionnement pour les moments au nu de l'appui monolithique selon 5.3.2.2
• Réduction des efforts tranchants au nu de l'appui et distance d selon 6.2.1(8)
• Le type de distribution de la section est à inertie variable au début de la barre, pour prendre en compte le changement de hauteur de la section.

résultats

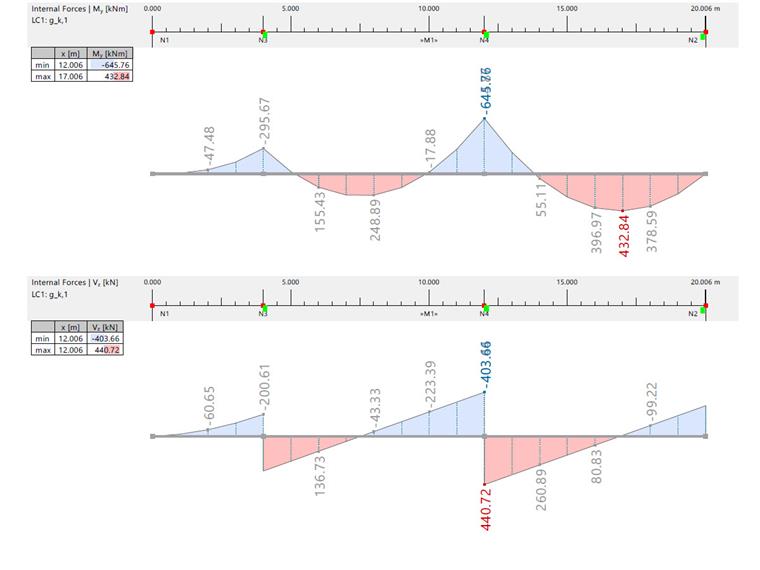
Moment fléchissant et effort tranchant des charges permanentes et imposées

Moment fléchissant et effort tranchant dûs à gk,1
Effort interne	Unité	RFEM / Solution analytique	Travée 1	Travée 2	Axe A	Axe B	Axe C
Moment fléchissant	[kNm]	RFEM	248,890	432,840	-296,460	-645,760	0
		Solution analytique	249 000	433,000	-296 000	-646 000	0
Effort tranchant	[kN]	RFEM	-43,330	80,830	-201,000/316,340	-403,660/440,720	-279,280
		Solution analytique	-44,000	81 000	-201 000/316 000	-404 000/441 000	-279,000

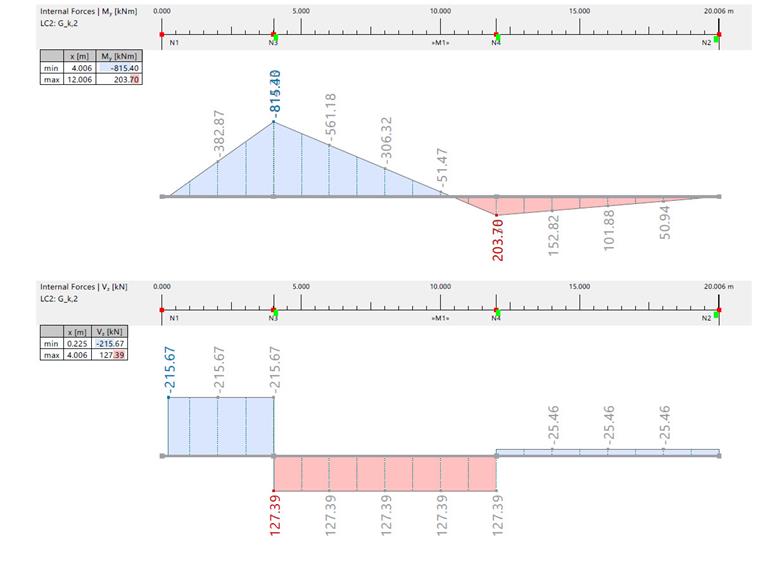
Moment fléchissant et effort tranchant dûs à Gk,2
Effort interne	Unité	RFEM / Solution analytique	Travée 1	Travée 2	Axe A	Axe B	Axe C
Moment fléchissant	[kNm]	RFEM	-305,850	101,850	-815,400	203,720	0
		Solution analytique	-306,000	102 000	-815,000	204 000	0
Effort tranchant	[kN]	RFEM	127,390	-25,460	-215,670/127,390	-127,390/-25,460	-25,460
		Solution analytique	127 000	-25 500	-216 000/127 000	-127 000/-25 500	-25 500

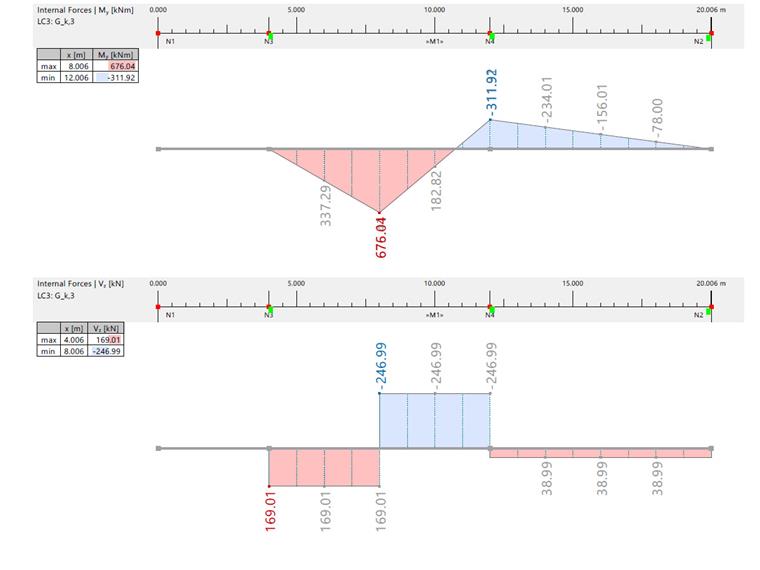
Moment fléchissant et effort tranchant dûs à Gk,3
Effort interne	Unité	RFEM / Solution analytique	Travée 1	Travée 2	Axe A	Axe B	Axe C
Moment fléchissant	[kNm]	RFEM	676,040	-155,960	0	-311,920	0
		Solution analytique	676 000	156 000	0	-312,000	0
Effort tranchant	[kN]	RFEM	169,010/-246,990	-38,990	169,010	-246 990/38,990	38,990
		Solution analytique	169 000/247 000	39 000	169 000	-247 000/39 000	39 000

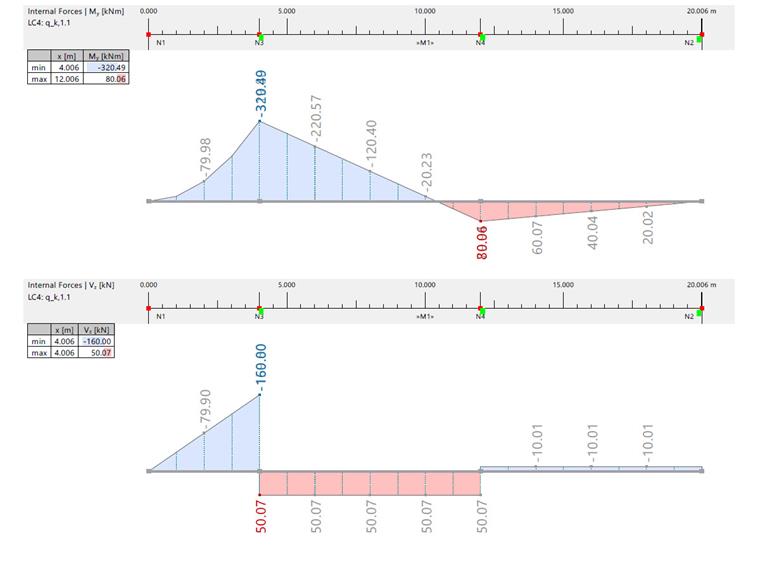
Moment fléchissant et effort tranchant dûs à qk,1,1
Effort interne	Unité	RFEM / Solution analytique	Travée 1	Travée 2	Axe A	Axe B	Axe C
Moment fléchissant	[kNm]	RFEM	-120,100	40 000	-320,200	79,950	0
		Solution analytique	-120,220	40,030	-320,490	80,060	0
Effort tranchant	[kN]	RFEM	50,070	-10 000	-160 000/50 020	50,020/-10,000	-10 000
		Solution analytique	50 000	-10,010	-160 000/50 070	50,070/-10,010	-10,010

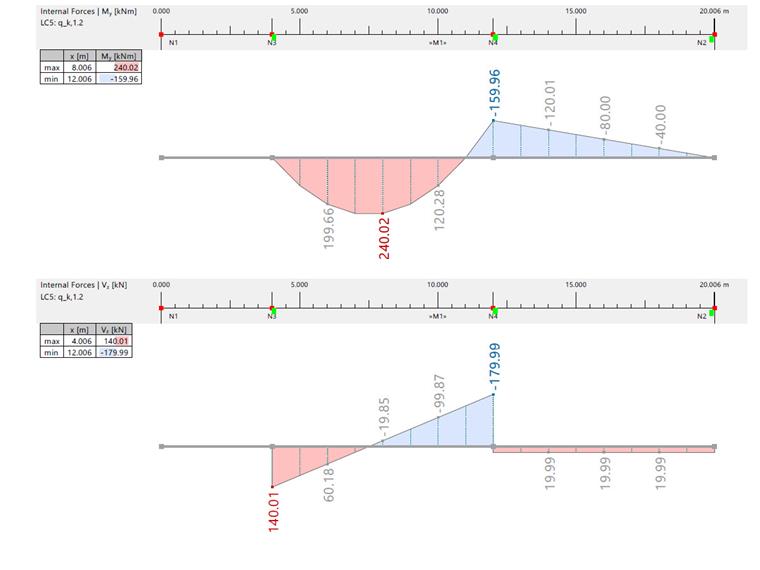
Moment fléchissant et effort tranchant dûs à à qk,1,2
Effort interne	Unité	RFEM / Solution analytique	Travée 1	Travée 2	Axe A	Axe B	Axe C
Moment fléchissant	[kNm]	RFEM	240,020	-79,980	0	-159,960	0
		Solution analytique	240 000	-80,000	0	-160 000	0
Effort tranchant	[kN]	RFEM	-19,990	19,990	140,010	-179,990/19,999	19,999
		Solution analytique	-20 000	20 000	140 000	-180 000/20 000	20 000

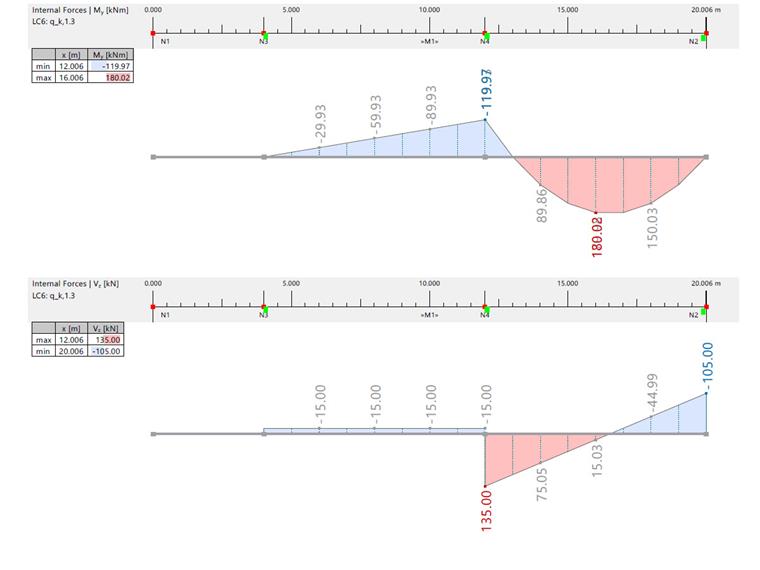
Moment fléchissant et effort tranchant dûs à qk,1,3
Effort interne	Unité	RFEM / Solution analytique	Travée 1	Travée 2	Axe A	Axe B	Axe C
Moment fléchissant	[kNm]	RFEM	-59,980	180,010	0	-119,970	0
		Solution analytique	-60 000	184 000	0	-120 000	0
Effort tranchant	[kN]	RFEM	-15 000	15 000	-15 000	-15 000/135 000	-105 000
		Solution analytique	-15 000	15 000	-15 000	-15 000/135 000	-105 000

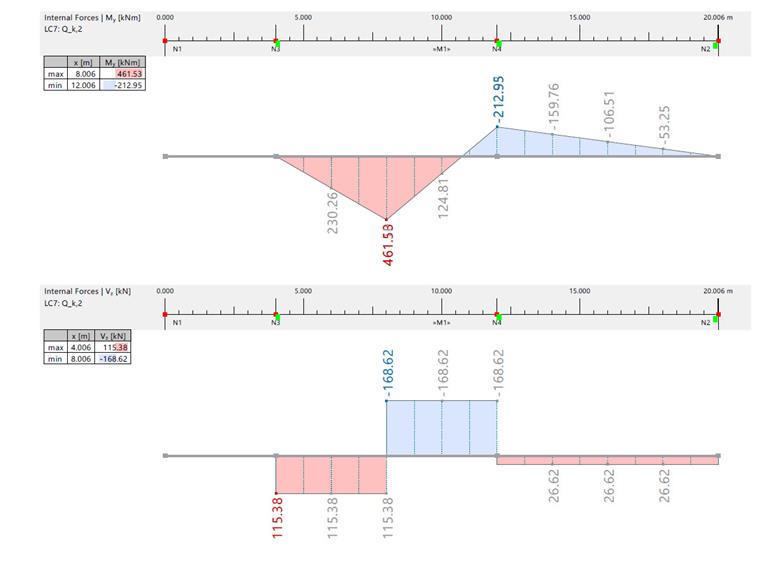
Moment fléchissant et effort tranchant dûs à Qk,2
Effort interne	Unité	RFEM / Solution analytique	Travée 1	Travée 2	Axe A	Axe B	Axe C
Moment fléchissant	[kNm]	RFEM	461,530	-106,470	0	-212,950	0
		Solution analytique	420 000	-106 500	0	-213,000	0
Effort tranchant	[kN]	RFEM	115,380/-168,620	26,620	115,380	-168,620/26,620	26,620
		Solution analytique	-169 000/115 000	26 600	115 000	-15 000/135 000	-169 000/26 600

<br/>

Efforts internes

Le tableau ci-dessous contient toutes les combinaisons de charges de l'état limite ultime :

Combinaison de charges	Cas de charge assignés
CO1	1,00 · CC1 + 1,00 · CC2 + 1,00 · CC3
CO2	1,35 · CC1 + 1,35 · CC2 + 1,35 · CC3 + 1,50 · CC4 + 1,50 · CC5 + 1,50 · CC6 + (1,50 · 0,80) · CC7
CO3	1,35 · CC1 + 1,35 · CC2 + 1,35 · CC3 + (1,50 · 0,70) · CC4 + (1,50 · 0,70) · CC5 + (1,50 · 0,70) · CC6 + 1,50 · CC7
CO4	1,35 · CC1 + 1,00 · CC2 + 1,35 · CC3 + 1,50 · CC5 + 1,50 · CC6 + (1,50 · 0,80) · CC7
CO5	1,35 · CC1 + 1,00 · CC2 + 1,35 · CC3 + (1,50 · 0,70) · CC5 + 1,50 · CC7
CO6	1,00 · CC1 + 1,35 · CC2 + 1,35 · CC3 + (1,50 · 0,70) · CC4 + 1,50 · CC7
CO7	1,35 · CC1 + 1,00 · CC2 + 1,35 · CC3 + (1,50 · 0,70) · CC5 + (1,50 · 0,70) · CC6 + 1,50 · CC7
CO8	1,35 · CC1 + 1,35 · CC2 + 1,00 · CC3 + 1,50 · CC4 + 1,50 · CC6
CO9	1,35 · CC1 + 1,35 · CC2 + 1,35 · CC3 + 1,50 · CC4 + 1,50 · CC5 + (1,50 · 0,80) · CC7

<br />

Action	Unité	Combinaisons de charge	Résultat dans RFEM	Résultat de référence	Ratio
MEd,A	kNm	CO8	-1981,830	-1980,000	1,00
MEd,B	kNm	CO4	-1 764,600	-1 765 000	0,99
MEd,1	kNm	CO5	1887,120	1 887 000	1,00
MEd,2	kNm	CO8	885,540	895 000	0,99
VEd,A,li	kN	CO2	-802,500	-803,000	0,99
VEd,A,re	kN	CO9	1 250,770	1 250 000	1,00
VEd,1,li	kN	CO6	582,090	581 000	1,00
VEd,1,re	kN	CO7	-554,660	-500,000	0,99
VEd,B,li	kN	CO4	-1245,820	-1 246 000	0,99
VEd,B,re	kN	CO4	-886,580	- 887,000	0,99
VEd,C	kN	CO8	-544,930	-545,000	0,99

</p> ==== Armatures longitudinales requises ====
Dans la littérature spécialisée, une redistribution de 15 % des moments a été considérée à l'appui B dans les combinaisons de charges 4 et une redistribution de 12 % des moments a été considérée dans la combinaison de charges 7. En revanche, RFEM applique la même redistribution des moments à toutes les combinaisons de charges. Il est nécessaire d'ajuster le modèle RFEM afin de faciliter une comparaison pertinente avec la littérature spécialisée. Ensuite, nous vous présenterons la solution réelle fournie par RFEM. Il est nécessaire d'ajuster le modèle RFEM afin de faciliter une comparaison pertinente avec la littérature spécialisée. Ensuite, nous vous présenterons la solution réelle fournie par RFEM.'''Comparaison des résultats de RFEM aux résultats de la littérature spécialisée :''''''Appui A :'''La poutre est reliée de manière monolithique à l'appui, ainsi, le moment critique de calcul se trouve au nu de l'appui. Cependant, la littérature néglige l'influence de la charge lors du calcul du moment au bord de l'appui. Pour pouvoir effectuer une comparaison pertinente avec les résultats de RFEM, il est nécessaire de recalculer le modèle en considérant l'influence de la charge. Le moment de calcul au nu de l'appui sans considération de l'influence de charge, MEd, est de -1819,0 kNm. En considérant l'effet des charges, MEd augmente jusqu'à -1823.0 kNm. Pour pouvoir effectuer une comparaison pertinente avec les résultats de RFEM, il est nécessaire de recalculer le modèle en considérant l'influence de la charge. Le moment de calcul au nu de l'appui sans considération de l'influence de charge, MEd, est de -1819,0 kNm. En considérant l'effet des charges, MEd augmente jusqu'à -1823.0 kNm. Le moment de calcul au nu de l'appui sans considération de l'influence de charge, M_Ed, est de -1819,0 kNm. En considérant l'effet des charges, MEd augmente jusqu'à -1823.0 kNm. En considérant l'effet des charges, M_Ed augmente jusqu'à -1823.0 kNm.

	RFEM		Solution analytique		Ratio
Cas de charge	Moment fléchissant de calcul MEd	Armatures requises As,stat,tot	Moment fléchissant de calcul MEd	Armatures requises As,stat,tot	MEd	As,stat,tot
	[kNm]	[cm2]	[kNm]	[cm2]	[kNm]	[cm2]
CO8	-1824,790	32,50	-1823,000	31,60	1,00	1,02

<br />In the literature, it is assumed that the cross-section height at the edge of the support is equal to the cross-section height at the middle of the support. Cependant, la hauteur réelle de la section est considérée dans RFEM en raison de la section à inertie variable. Les armatures requises sont donc plus élevées dans RFEM.Appui B :La combinaison de charges critique dans ce cas est la combinaison de charges 4. Le rapport de redistribution des moments dans l'appui B est de 0,850.

Appui B
	RFEM		Solution analytique		Ratio
Cas de charge	Moment fléchissant de calcul MEd	Armatures requises As,stat,tot	Moment fléchissant de calcul MEd	Armatures requises As,stat,tot	MEd	As,stat,tot
	[kNm]	[cm2]	[kNm]	[cm2]	[kNm]	[cm2]
CO4	-1345,870	22,40	-1360,000	22,80	0,99	0,98

<br />When calculating the design moment, the literature takes into consideration that the moment at the face of the support should not be less than 0.65 of the full fixed end moment (DIN EN 1992-1-1, 5.3.2.2). Cette condition n'est pas implémentée dans RFEM. Cela explique la différence sur le moment de calcul.

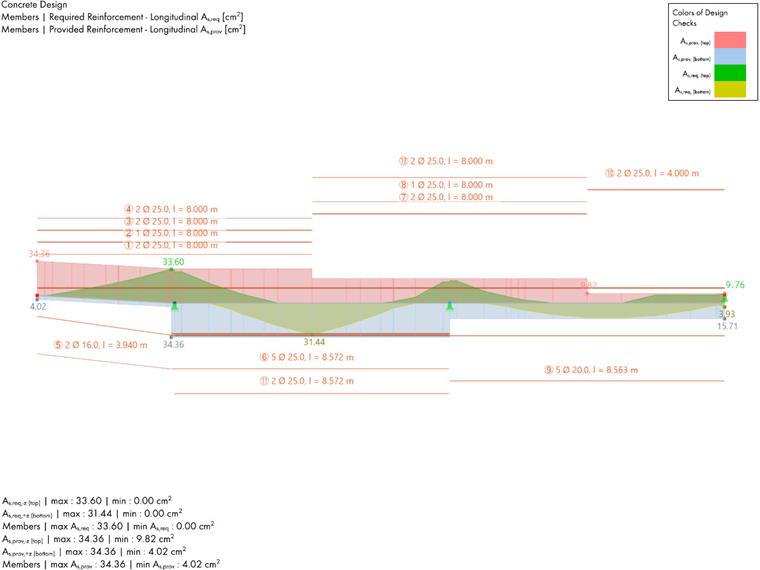
Travée 1 :

Comme la poutre est définie comme une barre continue dans RFEM, une largeur efficace b_eff ne peut pas être définie à chaque travée. La valeur la plus faible des deux largeurs efficaces des travées 1 et 2 est utilisée pour la simplification. b_eff est alors définie à 2,620 m.

La valeur la plus faible des deux largeurs efficaces des travées 1 et 2 est utilisée pour la simplification. b_eff est alors définie à 2,620 m. La littérature considère une redistribution des moments de 12 % pour la combinaison de charges 7, le rapport de redistribution des moments dans l'appui central est donc désormais défini sur 0,880.

Travée 1
	RFEM		Solution analytique		Ratio
Cas de charge	Moment fléchissant de calcul MEd	Armatures requises As,stat,tot	Moment fléchissant de calcul MEd	Armatures requises As,stat,tot	MEd	As,stat,tot
	[kNm]	[cm2]	[kNm]	[cm2]	[kNm]	[cm2]
CO7	1926,280	30,13	1927 000	33,10	0,99	0,91

<br />'''Span 2:'''<br />In this case, no moment redistribution is considered. Le rapport de redistribution des moments est défini sur 1 000.

Travée 2
	RFEM		Solution analytique		Ratio
Cas de charge	Moment fléchissant de calcul MEd	Armatures requises As,stat,tot	Moment fléchissant de calcul MEd	Armatures requises As,stat,tot	MEd	As,stat,tot
	[kNm]	[cm2]	[kNm]	[cm2]	[kNm]	[cm2]
CO8	885,520	13,79	895 000	15,10	0,99	0,91

<br>In the literature, the required longitudinal reinforcement is determined using approximation methods for T-beams according to DAstb-heft 425.

Dans cette méthode, la force de compression dans la semelle est supposée être au centre de la semelle (h_f/2). Dans RFEM, l'armature requise est déterminée à l'aide d'une analyse de section. Les armatures requises sont donc inférieures à ce qui est indiqué dans la littérature spécialisée.

Dans RFEM, l'armature requise est déterminée à l'aide d'une analyse de section. Les armatures requises sont donc inférieures à ce qui est indiqué dans la littérature spécialisée. Solution fournie par RFEMLa redistribution des moments dans l'appui central est désormais définie à 15 % pour toutes les combinaisons de charges. Les résultats sont résumés dans les tableaux ci-dessous. Les résultats sont résumés dans les tableaux ci-dessous.
'''Appui A :'''
Le cas de charge 8 produit le moment fléchissant le plus élevé et est donc déterminant.

Appui A
Cas de charge	Moment fléchissant de calcul MEd	Armatures requises As,stat,tot
	[kNm]	[cm2]
CO8	-1824,840	32,32

<br />'''Support B:'''<br />

Appui B :
Cas de charge	Moment fléchissant de calcul MEd	Armatures requises As,stat,tot
	[kNm]	[cm2]
CO4	-1345,890	22,40

<br />'''Span 1:'''<br /> When moment redistribution is taken into consideration in all load combinations, CO5 has the highest design bending moment in Span 1.<br />

Travée 1 :
Cas de charge	Moment fléchissant de calcul MEd	Armatures requises As,stat,tot
	[kNm]	[cm2]
CO5	2005,410	31,44

<br /> '''Span 2:'''<br />CO8 has a design moment after moment redistibution M_Ed of 940 kNm.<br />

Travée 2 :
Cas de charge	Moment fléchissant de calcul MEd	Armatures requises As,stat,tot
	[kNm]	[cm2]
CO8	940 000	14,73

==== Armatures d'effort tranchant ====
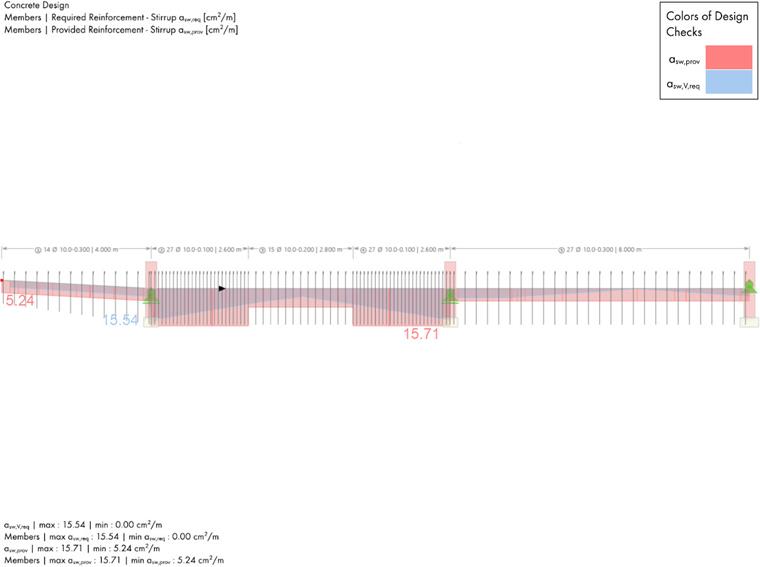
'''Armatures d'effort tranchant dans le porte-à-faux :'''
Pour déterminer les cadres requis dans le porte-à-faux, 3 positions sont examinées. Les résultats sont résumés dans le tableau ci-dessous :

Porte-à-faux
Position x	Paramètre	Symbole	Unité	RFEM	Solution analytique	Ratio
x = 0,45 m	Hauteur efficace	d	[m]	0,940	0,920	1,02
	Bras de levier interne	Z	[m]	0,848	0,828	1,02
	Effort tranchant	VEd	[kN]	-327,190	-328,000	0,99
	Moment fléchissant de calcul	MEd	[kNm]	-73,320	-74,000	0,99
	Composante d'effort tranchant de l'effort dans la zone en compression	Vccd	[kN]	12,550	13 000	0,99
	Effort tranchant de calcul	VEd,red	[kN]	314,640	314 000	1,0
	Capacité de cisaillement sans armature	Vrd,cc	[kN]	219,420	221,00	0,99
	Inclinaison de la bielle de compression	cot Θ	[-]	3,0	3,0	1,0
	Capacité de la bielle en compression	Vrd,max	[kN]	996,230	1003,000	0,99
	Armatures requises	asw,req	[cm2/m]	2,84	2,91	0,98
x = 1,37 m	Hauteur efficace	d	[m]	1,070	1,050	1,02
	Bras de levier interne	Z	[m]	0,965	0,945	1,02
	Effort tranchant	VEd	[kN]	-417,720	-418,000	1,00
	Moment fléchissant de calcul	MEd	[kNm]	-414,250	-415,000	1,00
	Composante d'effort tranchant de l'effort dans la zone en compression	Vccd	[kN]	50,000	66 000	0,94
	Effort tranchant de calcul	VEd,red	[kN]	355,510	353 000	1,01
	Capacité de cisaillement sans armature	Vrd,cc	[kN]	250,070	252 000	0,99
	Inclinaison de la bielle de compression	cot Θ	[-]	3,0	3,0	1,0
	Capacité de la bielle en compression	Vrd,max	[kN]	1135,860	1144 000	0,99
	Armatures requises	asw,req	[cm2/m]	2,83	2,86	0,99
x = 2,37 m	Hauteur efficace	d	[m]	1,210	1,190	1,02
	Bras de levier interne	Z	[m]	1,090	1,070	1,02
	Effort tranchant	VEd	[kN]	-541,800	-543,000	1,0
	Moment fléchissant de calcul	MEd	[kNm]	-891,790	-893,00	1,00
	Composante d'effort tranchant de l'effort dans la zone en compression	Vccd	[kN]	118,250	125 000	0,95
	Effort tranchant de calcul	VEd,red	[kN]	423,550	418.000	1,01
	Capacité de cisaillement sans armature	Vrd,cc	[kN]	283,220	285 000	0,99
	Inclinaison de la bielle de compression	cot Θ	[-]	3,0	3,0	1,0
	Capacité de la bielle en compression	Vrd,max	[kN]	1286,410	1298 000	0,99
	Armatures requises	asw,req	[cm2/m]	2,98	2,99	1,0

<br>'''Span 1:''' <br /> The decisive member location for the calculation of the stirrups in field 1 is at a distance d from the right edge of the support A.<br />

Travée 1
Paramètre	Symbole	Unité	RFEM	Solution analytique	Ratio
Hauteur efficace	d	[m]	1,440	1,430	1,00
Effort tranchant au niveau de l'appui A	VEd, A	[kN]	1 250,770	1 250 000	1,00
Effort tranchant de calcul	VEd,A,re	[kN]	952,430	954 000	1,00
Capacité de cisaillement sans armature	VRd,cc	[kN]	346,210	343 000	1,00
Inclinaison de la bielle de compression	cot Θ	[-]	1,88	1,87	1,00
Armatures d'effort tranchant requises	asw,req	[cm2/m]	8,95	9,11	0,98

<br>'''Span 2:'''<br>The calculation of the stirrups is done analog to span 1.<br />

Travée 2
Paramètre	Symbole	Unité	RFEM	Solution analytique	Ratio
Hauteur efficace	d	[m]	1,440	1,440	1,02
Effort tranchant au niveau de l'appui B	VEd,B	[kN]	886,580	855 000	1,03
Effort tranchant de calcul	VEd,B,re	[kN]	150,100	584 000	1,05
Capacité de cisaillement sans armature	VRd,cc	[kN]	346,210	343 000	1,00
Inclinaison de la bielle de compression	cot Θ	[-]	2,75	2,91	0,95
Armatures d'effort tranchant requises	asw,req	[cm2/m]	3,94	3,58	1,10

<br> Les différences dans les résultats de la travée 2 sont dues au fait que la littérature a considéré l'effort tranchant au niveau de l'appui B après redistribution des moments. Cependant, la redistribution des moments n'influence pas le calcul de l'effort tranchant dans RFEM.