Les imperfections sont généralement appliquées dans un calcul si l'équilibre des forces sur le système déformé est recherché pour les composants. Cette analyse géométriquement non-linéaire en combination avec les composants prédéformés évoqués précédemment prévoit des augmentations pour les efforts internes et les déformations en comparaison à l'analyse géométriquement linéaire. Toutefois, on peut réaliser avec ces augmentations des efforts internes et des déformations dans de nombreux cas un dimensionnement beaucoup plus efficient des composants de la structure par rapport à un dimensionnement simple, dans lequel l'imperfection du composant est considérée avec les coefficients d'amplification.
Les normes de calcul, telles que l'EN 1993-1-1, permettent de simuler les imperfections à l'aide de charges équivalentes. L'amplitude de la charge équivalente est définie par l'effort axial agissant du composant structural et son comportement au flambement.
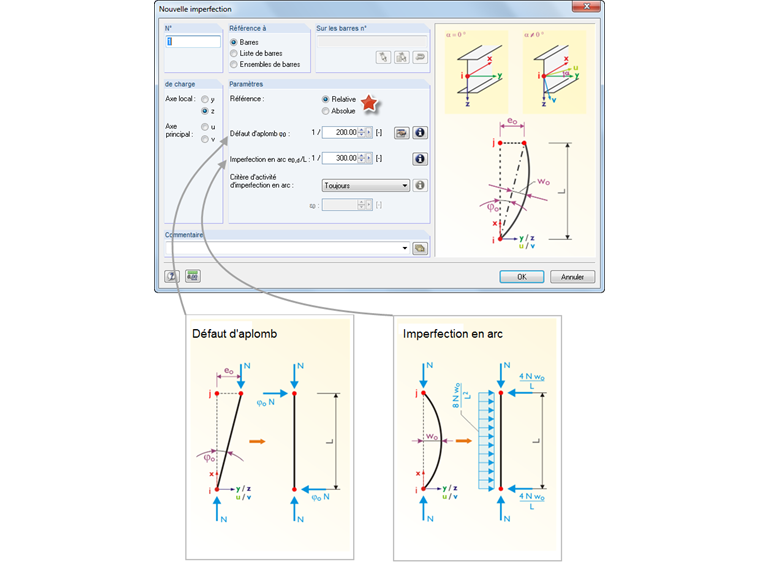
Afin de représenter autant que possible toute forme d'imperfection, il existe une imperfection d'inclinaison et une imperfection de pré-encombrement. L'imperfection d'inclinaison simule un composant comme incliné sur toute sa longueur. L'imperfection locale en arc simulée par contre une courbe décrivant le flamblement.
Nos programmes peuvent simuler ce genre d'imperfections par les imperfections de barre. Cette imperfection de barre est organisée dans le programme comme une charge. Cet attribut permet d'ajouter les imperfections comme cas de charge à ajouter d'autres séries de cas de charge. Ainsi, vous avez la possibilité de vérifier différentes géométries d'imperfections par différentes séries de cas de charge dans un modèle de calcul.
Exemple :
CC1 = Poids propre
CC2 = Charge imposée
CC3 = Imperfection dans la direction X
CC4 = Imperfection dans la direction Y
CO1 = 1,35 ⋅ CC1 + 1,5 ⋅ CC2 + 1,0 ⋅ CC3 ... Combinaison des cas de charge avec imperfection dans X
CO2 = 1,35 ⋅ CC1 + 1,5 ⋅ CC2 + 1,0 ⋅ CC4 ... Combinaison des cas de charge avec imperfection dans Y
Le programme détermine alors séparément pour chaque combinaison de cas de charge, la force normale et y ajoute le calcul de la charge équivalente. Étant donné que cette force normale peut changer en raison de l'analyse géométriquement non-linéaire dans les itérations respectives, la force normale est vérifiée et modifiée si nécessaire après chaque itération pour la charge équivalente d'imperfection. Pour les composants avec un diagramme d'effort normal variable, il est considéré la moyenne d'effort normal sur toute la longueur de la barre pour la charge d'imperfection.