Imperfekcje są często wykorzystywane w obliczeniach, gdy zachodzi potrzeba określenia równowagi sił dla elementów konstrukcyjnych w układzie odkształconym. To właśnie te nieliniowe obliczenia w połączeniu ze wspomnianym odkształceniem elementu konstrukcyjnego powodują wzrost sił wewnętrznych i odkształceń w porównaniu z obliczeniami liniowymi. Niemniej jednak, te zwiększone siły wewnętrzne i odkształcenia można w większości przypadków wykorzystać do uzyskania znacznie bardziej efektywnego wymiarowania elementu konstrukcyjnego w porównaniu z prostym obliczeniem, w którym imperfekcja elementu konstrukcyjnego jest uwzględniana za pomocą współczynników wzrostu.
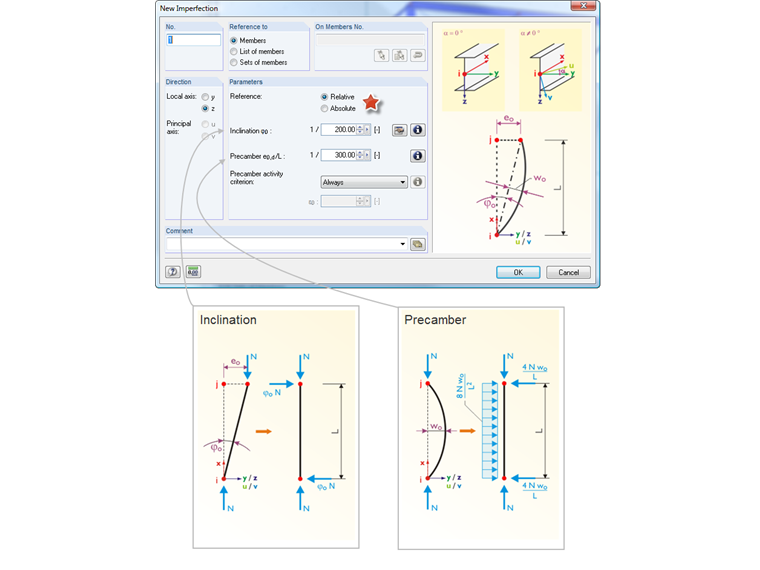
Normy projektowe, takie jak EN 1993-1-1, umożliwiają symulację imperfekcji za pomocą obciążeń zastępczych. Wielkość obciążenia równoważnego jest definiowana przez działającą siłę osiową elementu konstrukcyjnego oraz jego zachowanie wyboczeniowe.
Aby jak najlepiej odwzorować dowolną formę imperfekcji, stosuje się imperfekcję nachylenia i wygięcie wstępne. Imperfekcja pochylenia symuluje nachylenie elementu na całej jego długości. Imperfekcja wygięcia wstępnego symuluje prosty element konstrukcyjny jako łuk.
Nasze programy mogą symulować tego typu imperfekcje za pomocą imperfekcji prętów. Imperfekcje prętów są zorganizowane w programie jako obciążenie. Atrybut ten pomaga w dodawaniu imperfekcji prętowych jako przypadku obciążenia do innych serii przypadków obciążeń. Dzięki temu można sprawdzić różne geometrie imperfekcji według różnych serii przypadków obciążeń w modelu obliczeniowym.
Przykład:
PO1 = Ciężar własny
PO2 = obciążenie wymuszone
PO3 = Imperfekcja w kierunku X.
PO4 = Imperfekcja w kierunku Y.
KO1 = 1,35 ⋅ PO1 + 1,5 ⋅ PO2 + 1,0 ⋅ PO3 ... Kombinacja obciążeń z imperfekcją w X.
CO2 = 1,35 ⋅ PO1 + 1,5 ⋅ PO2 + 1,0 ⋅ PO4 ... Kombinacja obciążeń z imperfekcją w osi Y.
Następnie program określa siłę osiową osobno dla każdej kombinacji obciążeń i uwzględnia ją w obliczeniach obciążenia równoważnego. Ponieważ ta siła osiowa może zmieniać się w poszczególnych iteracjach z powodu obliczeń geometrycznych nieliniowych, siła osiowa dla obciążenia równoważnego imperfekcji jest sprawdzana i, w razie potrzeby, modyfikowana po każdej iteracji. W przypadku elementów konstrukcyjnych o zmiennym rozkładzie siły osiowej na całej długości pręta stosowana jest średnia siła osiowa dla obciążenia imperfekcyjnego.