User Story
Nel primo esempio, procediamo con una progettazione preliminare, concentrandoci in particolare sul calcolo della forza totale. Viene selezionato un piano quadrato 2D. Appartiene al Gruppo 1 del WTG-Merkblatt-M3:
- G1: Valori qualitativi con basse esigenze di accuratezza per l'uso nell'indagine di base o nella progettazione preliminare. Lo sforzo e i requisiti per il livello di dettaglio sono ridotti, poiché spesso non tutte le condizioni al contorno sono pienamente chiarite.
- R1: Solitaria (senza edifici circostanti), analisi delle singole direzioni del vento importanti.
- Z1: Valori medi statistici, a condizione che riguardino processi di flusso stazionari in cui le fluttuazioni (ad esempio, a causa della turbolenza di flusso in avvicinamento) possano essere sufficientemente catturate con altri mezzi.
- S1: Effetti statici. È sufficiente rappresentare il modello strutturale con il dettaglio meccanico necessario, ma senza proprietà di massa e smorzamento.
Le dimensioni dell'esempio sono riportate in Figura 1, e l'ipotesi di input è illustrata in Tabella 1:
Tabella 1: Dati di Input dell'Esempio di Verifica del Piano Quadrato 2D
| Modello | Piano quadrato 2D |
|---|---|
| Dimensione | a = 1 m |
| Velocità del vento di base | V = 30 m/s |
| Densità dell'aria | ρ = 1.225 kg/m³ |
| Risolutore | Basato sulla pressione |
| Modello di turbolenza | Costante k-ω SST |
| Categoria di terreno | 2 |
| Tipo di profilo di velocità del vento in RFEM | Picco |
| Algoritmo numerico | Algoritmo SIMPLE |
| Discretizzazione | Secondo Ordine |
| Pressione residua | 10⁻⁴ |
| Viscosità cinematica | ν = 1.5 × 10⁻⁵ |
In questo esempio, confronteremo i valori della forza del vento tra EN 1991-1-4 e RWIND. La formula della forza nel paragrafo 5.3 dell'Eurocodice è definita:
|
cscd |
Structural factor |
|
cf |
Force coefficient for the structure or structural element |
|
qp(ze ) |
Peak velocity pressure at reference height ze |
|
Aref |
Reference area of the structure or structural element |
I coefficienti di forza (d=b=1 → Cf,0=2.10) delle sezioni rettangolari con angoli affilati e senza flusso libero alle estremità possono essere ottenuti nella Figura 7.23 di EN 1991-1-4, e il fattore di riduzione (ψr) per una sezione quadrata con angoli arrotondati (r/b=0 → ψ r=1) può essere ottenuto dalla Figura 7.24 di EN 1991-1-4. Valori indicativi del fattore di effetto alle estremità ψλ=0.63 in funzione del rapporto di solidità φ=1 rispetto alla snellezza λ=2 possono essere ottenuti dalla Figura 7.36 di EN 1991-1-4.
Il coefficiente di forza cf degli elementi strutturali della sezione rettangolare con il vento che soffia normalmente su una superficie piatta dovrebbe essere determinato dall'Espressione (7.9) di EN 1991-1-4:
|
cf,0 |
The force coefficient of rectangular sections with sharp corners and without free-end flow |
|
ψr |
The reduction factor for square sections with rounded corners |
|
ψλ |
The end-effect factor for elements with free-end flow |
- Velocità del vento media
La velocità media del vento vm (ze) all'altezza di riferimento z_e dipende dalla rugosità del terreno, dall'orografia del terreno e dalla velocità del vento di base vb. È determinata usando l'equazione (4.3) di EN 1991-1-4:
- Turbolenza del vento
L'intensità di turbolenza Iv (ze) all'altezza di riferimento ze è definita come la deviazione standard della turbolenza divisa per la velocità media del vento. È calcolata in conformità con l'Equazione 4.7 di EN 1991-1-4. Per il caso esaminato ze inferiore a zmin:
- Pressione di velocità di base
La pressione di velocità di base q_b è la pressione corrispondente al momento del vento determinata alla velocità del vento di base vb. La pressione di velocità di base è calcolata secondo la relazione fondamentale specificata in EN1991 -14 §4.5(1):
dove ρ è la densità dell'aria in conformità con EN1991-1-4 §4.5(1). In questo calcolo, viene considerato il seguente valore ρ=1.225 kg/m3.
- Pressione di velocità di picco
La pressione di velocità di picco qp (ze) all'altezza di riferimento ze include fluttuazioni di velocità medie e a breve termine. È determinata secondo l'Equazione 4.8 di EN1991-1-4:
Poi la forza del vento può essere calcolata:
L'immagine 2 mostra uno studio sulla sensibilità della mesh in RWIND per la lastra 2D. Man mano che la densità della mesh aumenta dal 10% al 40%, il coefficiente di forza Cf diminuisce e si stabilizza a 1.23 dal 30% in poi, indicando risultati indipendenti dalla mesh e garantendo l'accuratezza della simulazione senza un raffinamento eccessivo.
Inoltre, lo studio della mesh computazionale deve essere eseguito secondo il seguente link:
Il WTG-Merkblatt M3 fornisce due metodi chiave per validare i risultati della simulazione. Il Metodo Hit Rate valuta quante delle valori simulati Pi corrispondono correttamente ai valori di riferimento Oi entro una tolleranza definita, utilizzando un approccio di classificazione binaria (colpo o manco). Questo approccio valuta l'affidabilità della simulazione calcolando un tasso di successo q, simile alle funzioni di confidenza utilizzate nella teoria dell'affidabilità. Al contrario, il metodo dell' Errore Quadratico Medio Normalizzato (e2) offre una valutazione più dettagliata dell'accuratezza quantificando la deviazione quadratica media tra i valori simulati e quelli di riferimento, normalizzata per tenere conto delle differenze di scala. Insieme, queste metodi forniscono misure sia qualitative che quantitative per la validazione della simulazione.
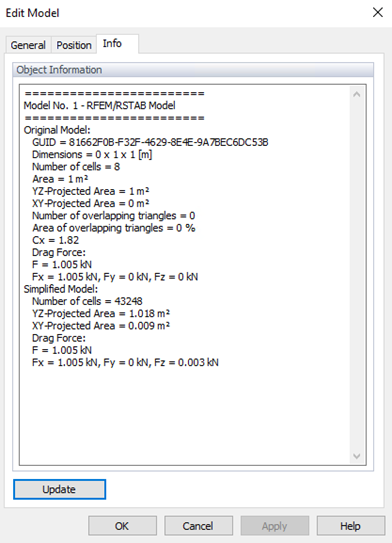
Risultati in RWIND e Confronto con Eurocodice
In RWIND i risultati delle forze totali (nelle Figure 3 e 4) sono disponibili nella scheda Info dell'Edit modello. La differenza tra RWIND e l'Eurocodice è di circa Wrel = 2.45% (inferiore ai criteri menzionati nel WTG); quindi il tasso di successo può essere ottenuto come q=100%, il che mostra un buon accordo. Il basso errore quadrato medio normalizzato e2=0.0005 conferma un forte accordo tra simulazione e misurazioni, soddisfacendo efficacemente gli standard di validazione.
Ecco il modello 3D della lastra 2D: