Histoire d’utilisateur
Dans le premier exemple, nous procédons à un calcul préliminaire, en nous concentrant particulièrement sur le calcul de la force totale. Il est sélectionné comme un plan carré 2D. Il appartient au Groupe 1 du WTG-Merkblatt-M3 :
- G1 : valeurs qualitatives avec des exigences de précision faibles pour une utilisation dans l’étude de base ou le calcul préliminaire. L’effort et les exigences pour le niveau de détail sont réduits, car les conditions limites ne sont souvent pas entièrement clarifiées.
- R1 : isolée (sans bâtiments environnants), analyse de chaque directions de vent importante.
- Z1 : valeurs moyennes statistiques, à condition qu’elles concernent des écoulements stationnaires où les fluctuations (par exemple, dues à la turbulence de l’écoulement approchant) peuvent être suffisamment capturées par d’autres mesures.
- S1 : effets statiques. Représenter le modèle structurel avec le détail mécanique requis, mais sans propriétés de masse et d’amortissement suffit.
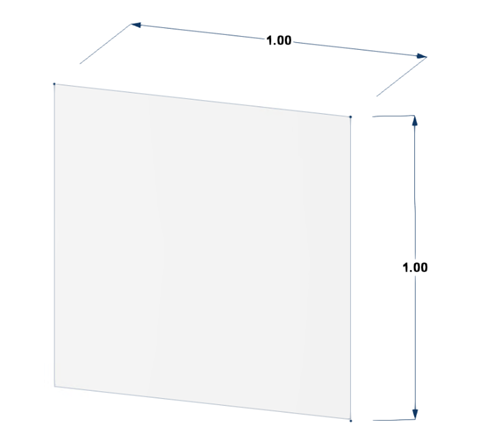
Les dimensions de l’exemple sont montrées à la figure 1, et l’hypothèse d’entrée est illustrée dans le Tableau 1 :
Table 1 : Données d’entrée de l’exemple de vérification du plan carré 2D
| Modèle | Plan carré 2D |
|---|---|
| Dimension | a = 1 m |
| Vitesse de base du vent | V = 30 m/s |
| Densité de l’air | ρ = 1,225 kg/m³ |
| Solveur | Basé sur la pression |
| Modèle de turbulence | k-ω SST stable |
| Catégorie de terrain | 2 |
| Type de profil de vitesse de vent dans RFEM | Pic |
| Algorithme numérique | Algorithme SIMPLE |
| Discrétisation | Ordre deux |
| Pression résiduelle | 10⁻⁴ |
| Viscosité cinématique | ν = 1,5 × 10⁻⁵ |
Dans cet exemple, nous allons comparer les valeurs de la force du vent entre EN 1991-1-4 et RWIND. La formule de la force du vent dans la clause 5.3 de l’Eurocode est définie :
|
cscd |
Structural factor |
|
cf |
Force coefficient for the structure or structural element |
|
qp(ze ) |
Peak velocity pressure at reference height ze |
|
Aref |
Reference area of the structure or structural element |
Les coefficients de force (d=b=1 → Cf,0=2,10) des sections rectangulaires avec des coins vifs et sans écoulement à l’extrémité libre peuvent être obtenus dans la figure 7.23 de l’EN 1991-1-4, et le facteur de réduction (ψr) pour une section carrée à coins arrondis (r/b=0 → ψ r=1) peut être obtenu de la figure 7.24 de l’EN 1991-1-4. Des valeurs indicatives du facteur d’effet d’extrémité ψλ=0,63 en fonction du rapport de solidité φ=1 par rapport à l’élancement λ=2 peuvent être obtenues dans la figure 7.36 de l’EN 1991-1-4.
Le coefficient de force cf des éléments structurels de la section rectangulaire avec le vent soufflant normalement sur une surface plate doit être déterminé par l’Expression (7.9) de l’EN 1991-1-4 :
|
cf,0 |
The force coefficient of rectangular sections with sharp corners and without free-end flow |
|
ψr |
The reduction factor for square sections with rounded corners |
|
ψλ |
The end-effect factor for elements with free-end flow |
- Vitesse moyenne du vent
La vitesse moyenne du vent vm (ze) à la hauteur de référence z_e dépend de la rugosité du terrain, de l’orographie du terrain, et de la vitesse de base du vent vb. Elle est déterminée à l’aide de l’équation (4.3) de l’EN 1991-1-4 :
- Turbulence du vent
L’intensité de la turbulence Iv (ze) à la hauteur de référence ze est définie comme l’écart type de la turbulence divisé par la vitesse moyenne du vent. Elle est calculée conformément à l’équation 4.7 de l’EN 1991-1-4. Pour le cas examiné, ze est inférieur à zmin :
- Pression dynamique de base
La pression dynamique de base q_b est la pression correspondant à la quantité de vent déterminée à la vitesse de base du vent vb. La pression dynamique de base est calculée selon la relation fondamentale spécifiée dans l’EN1991 -14 §4.5(1) :
où ρ est la densité de l’air selon l’EN1991-1-4 §4.5(1). Dans ce calcul, la valeur suivante est considérée ρ=1,225 kg/m3.
- Pression dynamique de pointe
La pression dynamique de pointe qp (ze) à la hauteur de référence ze inclut les fluctuations de vitesse moyennes et à court terme. Elle est déterminée selon l’équation 4.8 de l’EN1991-1-4 :
Ensuite, la force du vent peut être calculée :
La figure 2 montre une étude de sensibilité du maillage dans RWIND pour la plaque 2D. À mesure que la densité du maillage augmente de 10 % à 40 %, le coefficient de force Cf diminue et se stabilise à 1,23 à partir de 30 %, indiquant des résultats indépendants du maillage et assurant la précision de la simulation sans raffinement inutile.
De plus, l’étude du maillage numérique doit être effectuée selon le lien suivant :
WTG-Merkblatt M3 fournit deux méthodes clés pour valider les résultats de simulation. La méthode du taux de réussite évalue combien des valeurs simulées Pi correspondent correctement aux valeurs de référence Oi dans une tolérance définie, en utilisant une approche de classification binaire (succès ou échec). Cette approche évalue la fiabilité de la simulation en calculant un taux de réussite q, similaire aux fonctions de confiance utilisées en théorie de la fiabilité. En revanche, la méthode Erreur quadratique moyenne normalisée (e2) offre une évaluation de la précision plus détaillée en quantifiant la déviation quadratique moyenne entre les valeurs simulées et de référence, normalisée pour tenir compte des différences d’échelle. Ensemble, ces méthodes fournissent des mesures qualitatives et quantitatives pour la validation de la simulation.
Résultats dans RWIND et comparaison à l’Eurocode
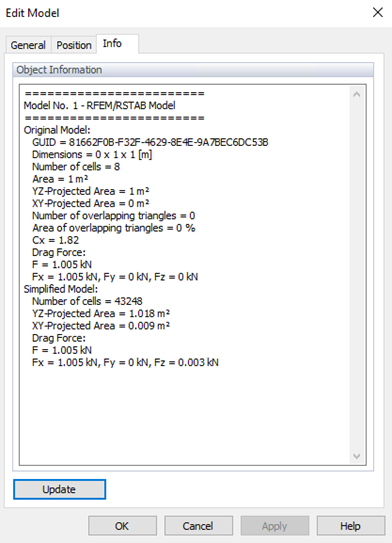
Dans RWIND, les résultats des forces totales (dans les figures 3 et 4) sont disponibles dans l’onglet Info de la boite de dialogue de modification du modèle. La différence entre RWIND et l’Eurocode est d'environ Wrel = 2,45% (inférieure au critère mentionné dans WTG). Alors le taux de réussite peut être obtenu comme q=100%, ce qui montre une bonne concordance. La faible erreur quadratique moyenne normalisée e²=0,0005 confirme une concordance solide entre la simulation et les mesures, répondant efficacement aux normes de validation.
Voici le modèle 3D de la plaque 2D :