User Story
Im ersten Beispiel fahren wir mit einem vorläufigen Entwurf fort und konzentrieren uns dabei insbesondere auf die Berechnung der Gesamtkraft. Es wird als 2D-Quadratebene ausgewählt. Die Einordnung erfolgt entsprechend der Gruppe 1 des WTG-Merkblatts M3:
- G1: Es handelt sich um qualitative Werte mit geringen Genauigkeitsanforderungen, die in der Basisuntersuchung oder im Vorentwurf verwendet werden. Da oft nicht alle Randbedingungen vollständig geklärt sind, werden der Aufwand und die Anforderungen an den Detaillierungsgrad reduziert.
- R1: Einzeln (ohne umliegende Gebäude), Analyse einzelner wichtiger Windrichtungen.
- Z1: Statistische Mittelwerte können verwendet werden, sofern es sich um stationäre Strömungsprozesse handelt und Schwankungen (z. B. aufgrund sich nähernder Strömungsturbulenzen) durch andere Messungen ausreichend erfasst werden können.
- S1: Statische Effekte. Es ist ausreichend, das Strukturmodell mit den erforderlichen mechanischen Details darzustellen – allerdings ohne Masse- und Dämpfungseigenschaften.
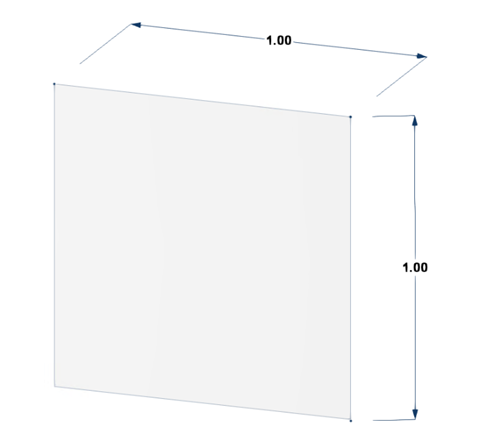
Die Abmessungen des Beispiels sind in Bild 1 dargestellt und die Eingangsannahme ist in Tabelle 1 veranschaulicht.
Tabelle 1: Tabelle 1: Eingabedaten des Verifizierungsbeispiels für die 2D-Quadratfläche
| Modell | 2D-Quadratfläche |
|---|---|
| Abmessung | a = 1 m |
| Basiswindgeschwindigkeit | V = 30 m/s |
| Luftdichte | ρ = 1,225 kg/m³ |
| Solver | Druckbasiert |
| Turbulenzmodell | Stationär k-ω SST |
| Geländekategorie | 2 |
| Typ des Windgeschwindigkeitsprofils in RFEM | Spitze |
| Numerischer Algorithmus | SIMPLE-Algorithmus |
| Diskretisierung | Zweiter Ordnung |
| Restdruck | 10⁻⁴ |
| Kinematische Viskosität | ν = 1,5 × 10⁻⁵ |
In diesem Beispiel werden die Windkraftwerte zwischen EN 1991-1-4 und RWIND verglichen. Die Windkraftformel ist im Abschnitt 5.3 der Eurocode-Norm definiert:
|
cscd |
Structural factor |
|
cf |
Force coefficient for the structure or structural element |
|
qp(ze ) |
Peak velocity pressure at reference height ze |
|
Aref |
Reference area of the structure or structural element |
Die Kraftbeiwerte (d=b=1 → Cf,0=2,10) von rechteckigen Querschnitten mit scharfen Kanten und ohne freie Endströmung können Bild 7.23 in EN 1991-1-4 entnommen werden. Der Reduktionsbeiwert (ψr) für einen quadratischen Querschnitt mit abgerundeten Kanten (r/b=0 → ψ r=1) kann nach Bild 7.24 in EN 1991-1-4 ermittelt werden. Indikative Werte des Abminderungsfaktors ψλ=0,63 in Abhängigkeit des Völligkeitsgrads φ=1 im Vergleich zur Schlankheit λ=2 sind in Bild 7.36 in EN 1991-1-4 zu finden.
Der Kraftbeiwert cf der Strukturelemente des rechteckigen Abschnitts bei normal auf einer ebenen Fläche einwirkendem Wind sollte gemäß Ausdruck (7.9) in EN 1991-1-4 ermittelt werden:
|
cf,0 |
The force coefficient of rectangular sections with sharp corners and without free-end flow |
|
ψr |
The reduction factor for square sections with rounded corners |
|
ψλ |
The end-effect factor for elements with free-end flow |
- Mittlere Windgeschwindigkeit
Die mittlere Windgeschwindigkeit vm (ze) in der Referenzhöhe z_e hängt von der Geländerauigkeit, der Geländeorographie und der grundlegenden Windgeschwindigkeit vb ab. Sie kann mit der Gleichung EN 1991-1-4 (4.3) berechnet werden:
- Windturbulenz
Die Turbulenzintensität Iv (ze) bei der Referenzhöhe ze ist definiert als die Standardabweichung der Turbulenz , dividiert durch die mittlere Windgeschwindigkeit. Sie wird gemäß Gleichung 4.7 in EN 1991-1-4 berechnet. Für den untersuchten Fall ze kleiner als zmin:
- Basisgeschwindigkeitsdruck
Der Basisgeschwindigkeitsdruck q_b ist der Druck, der dem Windimpuls entspricht, der bei der Basiswindgeschwindigkeit vb ermittelt wird. Der Basisgeschwindigkeitsdruck wird gemäß der in EN1991-14 §4.5(1) festgelegten Grundbeziehung berechnet:
wobei ρ die Dichte der Luft gemäß EN1991-1-4 §4.5(1) ist. In dieser Berechnung wird der folgende Wert berücksichtigt: ρ=1,225 kg/m3.
- Spitzengeschwindigkeitsdruck
Der Spitzengeschwindigkeitsdruck qp (ze) bei Referenzhöhe ze umfasst mittlere und kurzfristige Geschwindigkeitsschwankungen. Er wird gemäß EN1991-1-4-Gleichung 4.8 ermittelt:
Die Windkraft kann anschließend wie folgt berechnet werden:
Bild 2 zeigt eine Studie zur Netzempfindlichkeit in RWIND für die 2D-Platte. Mit zunehmender Netzdichte von 10 % auf 40 % verringert sich der Kraftbeiwert Cf und stabilisiert sich ab 30 % bei 1,23. Dies zeigt netzunabhängige Ergebnisse an und sichert die Simulationsgenauigkeit, ohne dass eine unnötige Verfeinerung erforderlich ist.
Die Durchführung der Studie des Berechnungsnetzes erfolgt außerdem über den folgenden Link:
Das WTG-Merkblatt M3 stellt zwei Schlüsselmethoden zur Validierung von Simulationsergebnissen vor. Die Methode „Trefferquote” nutzt einen binären Klassifizierungsansatz (Treffer oder Fehlschlag), um zu ermitteln, wie viele der simulierten Werte Pi innerhalb einer definierten Toleranz mit den Referenzwerten Oi übereinstimmen. Dieser Ansatz bewertet die Zuverlässigkeit der Simulation, indem er eine Trefferquote q berechnet, die den in der Zuverlässigkeitstheorie verwendeten Konfidenzfunktionen ähnelt. Im Gegensatz dazu bietet die Methode Normalisierte mittlere quadratische Abweichung (e2) eine detailliertere Genauigkeitsbewertung, indem sie die durchschnittliche quadratische Abweichung zwischen simulierten und Referenzwerten quantifiziert, normalisiert, um Skalenunterschiede zu berücksichtigen. Zusammen liefern diese Methoden somit sowohl qualitative als auch quantitative Messungen zur Simulationsvalidierung.
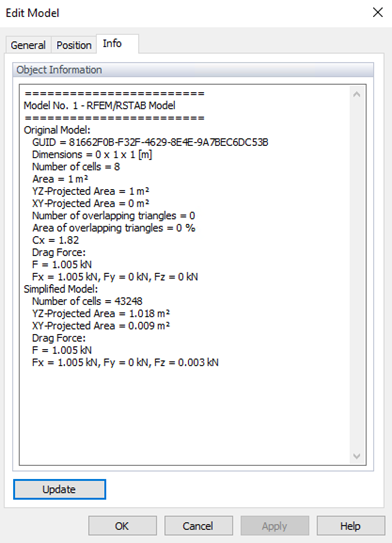
Ergebnisse in RWIND und Vergleich zum Eurocode
Die Ergebnisse der Gesamtkräfte (siehe Bilder 3 und 4) sind im Info-Tab „Modell bearbeiten” von RWIND verfügbar. Der Unterschied zwischen RWIND und dem Eurocode beträgt etwa Wrel = 2,45% (weniger als das erwähnte Kriterium in WTG). Dann kann die Trefferquote als q=100% ermittelt werden, was eine gute Übereinstimmung aufzeigt. Der niedrige normalisierte mittlere quadratische Fehler e2=0,0005 bestätigt eine starke Übereinstimmung zwischen Simulation und Messungen, wodurch die Validierungsstandards effektiv erfüllt werden.
Hier ist das 3D-Modell der 2D-Platte: