Zpět k online manuálům

115x

005874

Mahyar Kazemian, M.Sc.

7.11.2024

Vybrat manuál

Přehled

A. Obecné informace

např. Proudění větru, účinky větru a numerická simulace

C. WTG směrnice M3 pro numerickou simulaci proudění větru

C1. Účel a obsah směrnice
C2. Přiřazení úlohy pro požadované CFD modelování
- C2.1 Přidělení výpočetních metod k požadavkům prozkoumání
- C2.2 Požadavky na numerická šetření

D. Poznámky k CFD modelování

E. Praktické využití výsledků výpočtové simulace dynamiky tekutin

F. Dokumentace

G. Zajištění kvality

H. Příklady

I. Reference

H1.1. 2D čtvercová rovina

Uživatelský příběh

V prvním příkladu postupujeme s předběžným návrhem, zaměřujeme se především na výpočet celkové síly. Je vybrána jako 2D čtvercová rovina. Patří do Skupiny 1 WTG-Merkblatt-M3:

G1: Kvalitativní hodnoty s nízkými požadavky na přesnost pro použití v základním průzkumu nebo předběžném návrhu. Úsilí a požadavky na úroveň detailu jsou sníženy, protože často nejsou všechny okrajové podmínky plně vyjasněny.
R1: Samostatná (bez okolních budov), analýza jednotlivých důležitých směrů větru.
Z1: Statistické průměrné hodnoty, pokud se jedná o stacionární proudění, kde mohou být fluktuace (např. v důsledku turbulence přibližujícího se proudění) dostatečně pokryty jinými opatřeními.
S1: Statické účinky. Je dostačující reprezentovat konstrukční model s nezbytnými mechanickými detaily, ale bez hmotnosti a vlastností tlumení.

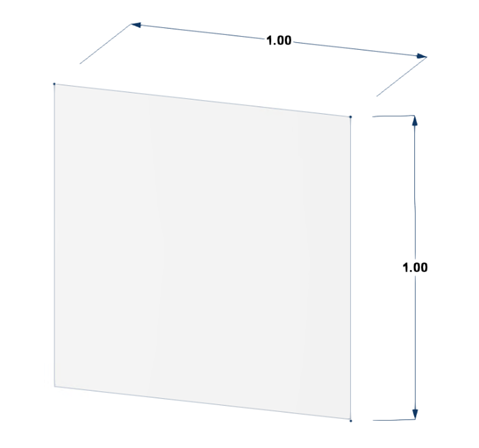
Rozměry příkladu jsou zobrazeny na obrázku 1 a vstupní předpoklad je ilustrován v tabulce 1:

1 Rozměry čtvercové 2D roviny (m)

Tabulka 1: Vstupní data ověřovacího příkladu 2D čtvercové roviny

Model	2D čtvercová rovina
Rozměr	a = 1 m
Základní rychlost větru	V = 30 m/s
Hustota vzduchu	ρ = 1.225 kg/m³
Solver	Na bázi tlaku
Model turbulence	Steady k-ω SST
Kategorizace terénu	2
Typ profilu rychlosti větru v RFEM	Špička
Numerický algoritmus	SIMPLE algoritmus
Diskretizace	Druhá řada
Zbytkový tlak	10⁻⁴
Kinematická viskozita	ν = 1.5 × 10⁻⁵

V tomto příkladu porovnáme hodnoty větrné síly mezi EN 1991-1-4 a RWIND. Vzorec pro větrnou sílu v Eurokódu, oddíl 5.3, je definován:

F_{w} = c_{s} c_{d} \cdot c_{f} \cdot q_{p} (z_{e}) \cdot A_{ref}

c_sc_d	Structural factor
c_f	Force coefficient for the structure or structural element
q_p(z_e )	Peak velocity pressure at reference height z_e
A_ref	Reference area of the structure or structural element

Síla větru v Eurokódu

Sílové koeficienty (d=b=1 → C_f,0=2.10) obdélníkových profilů s ostrými rohy a bez volného proudění na konci lze získat na obrázku 7.23 v EN 1991-1-4 a redukční faktor (ψ_r) pro čtvercový průřez se zaoblenými rohy (r/b=0 → ψ _r=1) lze získat z obrázku 7.24 v EN 1991-1-4. Orientační hodnoty faktoru koncového efektu ψ_λ=0.63 jako funkce poměru plnosti φ=1 oproti štíhlosti λ=2 lze získat na obrázku 7.36 v EN 1991-1-4.

Sílový koeficient c_f konstrukčních prvků obdélníkového průřezu s větrem foukajícím normálně na plochý povrch by měl být určen podle výrazu (7.9) v EN 1991-1-4:

C_{f} = C_{f . 0} \cdot ψ_{r} \cdot ψ_{λ} \to C_{f} = 2, 10 \times 1 \times 0, 63 = 1, 31

c_f,0	The force coefficient of rectangular sections with sharp corners and without free-end flow
ψ_r	The reduction factor for square sections with rounded corners
ψ_λ	The end-effect factor for elements with free-end flow

Součinitel síly konstrukčních prvků

Střední rychlost větru

Střední rychlost větru v_m (z_e) v referenční výšce z_e závisí na drsnosti terénu, orografii terénu a základní rychlosti větru v_b. Je určena pomocí rovnice (4.3) EN1991-1-4:

v_{m} (z_{e}) = c_{r} (z_{e}) \cdot c_{0} (z_{e}) \cdot v_{b} = 0, 7009 \cdot 1, 000 \cdot 30, 00 m / s = 21, 03 m / s

Střední rychlost větru

Turbulence větru

Intenzita turbulence I_v (z_e) v referenční výšce z_e je definována jako standardní odchylka turbulence dělená střední rychlostí větru. Vypočítává se podle rovnice 4.7 EN1991-1-4. Pro zkoumaný případ z_e menší než z_min:

\begin{aligned} I_{v} (z_{e}) = k_{1} / [c_{0} (z_{e}) \cdot \ln (max \{z_{e}, z_{min}\} / z_{0})] \\ = 1.000 / [1.000 \cdot \ln (max {1.000 m, 2.0 m} / 0.050 m)] = 0.2711 \end{aligned}

Turbulence větru

Základní tlak rychlosti

Základní tlak rychlosti q_b je tlak odpovídající momentu větru určený při základní rychlosti větru v_b. Základní tlak rychlosti je vypočítán podle základního vztahu specifikovaného v EN1991-14 §4.5(1):

q_{b} = (1 / 2) \cdot ρ \cdot v_{b}^{2} = (1 / 2) \cdot 1.23 kg / m^{3} \cdot (30.00 m / s)^{2} = 551 N / m^{2} = 0.551 kN / m^{2}

Základní dynamický tlak

kde ρ je hustota vzduchu v souladu s EN1991-1-4 §4.5(1). Při tomto výpočtu se uvažuje hodnota ρ=1.225 kg/m³.

Špičkový tlak rychlosti

Špičkový tlak rychlosti q_p (z_e) v referenční výšce z_e zahrnuje střední krátkodobé fluktuace rychlosti. Je určen podle rovnice 4.8 v EN1991-1-4:

\begin{aligned} q_{p} (z_{e}) = (1 + 7 \cdot ρ_{v} (z_{e})) \cdot (1 / 2) \cdot ρ \cdot v_{m} {(z_{e})}^{2} \\ = (1 + 7 \cdot 0.2711) \cdot (1 / 2) \cdot 1.23 kg / m^{3} \cdot (21.03 m / s)^{2} = 785 N / m^{2} \end{aligned}

Maximální dynamický tlak

Poté lze vypočítat větrnou sílu:

F_{w} = c_{s} c_{d} \cdot c_{f} \cdot q_{p} (z_{e}) \cdot A_{ref} \to F_{w} = 1 \times 1.31 \times 785 \times 1 = 1030 N

Síla od větru

Obrázek 2 ukazuje studii citlivosti sítě v RWIND pro 2D desku. Jak se hustota sítě zvyšuje z 10% na 40%, koeficient síly C_f klesá a stabilizuje se na 1.23 od 30% výše, což naznačuje výsledky nezávislé na síti a zajišťuje přesnost simulace bez zbytečného zpřesnění.

Studie citlivosti sítě s vizualizací efektů na 2D desku v programu RWIND se zaměřením na změny hustoty sítě.

2 Studie citlivosti sítě v programu RWIND pro 2D desku

Studie početní sítě musí být také provedena podle následujícího odkazu:

Studie výpočtové sítě

WTG-Merkblatt M3 poskytuje dvě klíčové metody pro validaci výsledků simulace. Metoda Hit Rate hodnotí, kolik simulovaných hodnot P_i se správně shoduje s referenčními hodnotami O_i v definované toleranci pomocí binárního klasifikačního přístupu (zásah nebo chybný zásah). Tento přístup hodnotí spolehlivost simulace výpočtem hit rate q, podobně jako funkce důvěry používané v teorii spolehlivosti. Naopak metoda Normalizované střední čtvercové chyby (e²) nabízí podrobnější hodnocení přesnosti kvantifikací průměrné čtvercové odchylky mezi simulovanými a referenčními hodnotami, normalizovanou pro zohlednění rozdílů v měřítku. Tyto metody dohromady poskytují jak kvalitativní, tak kvantitativní měření pro validaci simulace.

Validace výsledků simulace pomocí metody hit rate popsané v dokumentu WTG-Merkblatt M3

Vyhodnocení přesnosti výsledků pomocí normalizované střední kvadratické chyby definované ve WTG-Merkblatt M3

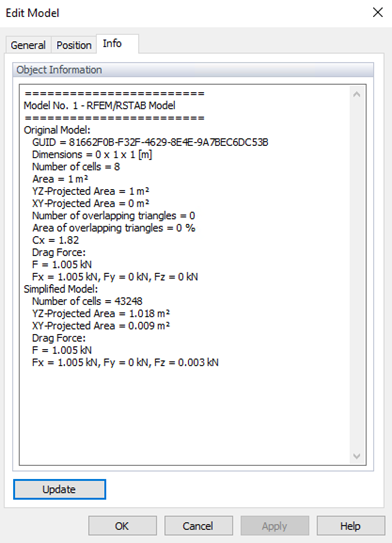
Výsledky v RWIND a porovnání s Eurokódem

V RWIND jsou výsledky celkových sil (na obrázcích 3 a 4) dostupné na kartě Info při úpravě modelu. Rozdíl mezi RWIND a Eurokódem je asi W_rel = 2.45% (méně než uvedené kritérium v WTG); poté může být hodnocení zásahu získáno jako q=100%, což ukazuje na dobrou shodu. Nízká normalizovaná střední čtvercová chyba e2=0.0005 potvrzuje silnou shodu mezi simulací a měřeními, účinně splňujícími validační standardy.