User Story
W pierwszym przykładzie przechodzimy do wstępnego projektu, koncentrując się szczególnie na obliczaniu siły całkowitej. Jest to wybrany jako 2D kwadratowa płaszczyzna. Należy do Grupy 1 WTG-Merkblatt-M3:
- G1: Wartości jakościowe z niskimi wymaganiami dokładności do wykorzystania w podstawowym badaniu lub wstępnym projektowaniu. Wysiłek i wymagania dotyczące poziomu szczegółowości są zredukowane, ponieważ często nie wszystkie warunki brzegowe są w pełni wyjaśnione.
- R1: Samotna (bez otaczających budynków), analiza pojedynczych ważnych kierunków wiatru.
- Z1: Wartości średnie statystyczne, pod warunkiem, że dotyczą stacjonarnych procesów przepływu, gdzie wahania (np. spowodowane turbulencjami napływu) mogą być wystarczająco uchwycone innymi środkami.
- S1: Efekty statyczne. Wystarczy przedstawić model konstrukcyjny z niezbędnymi detalami mechanicznymi, ale bez właściwości masy i tłumienia.
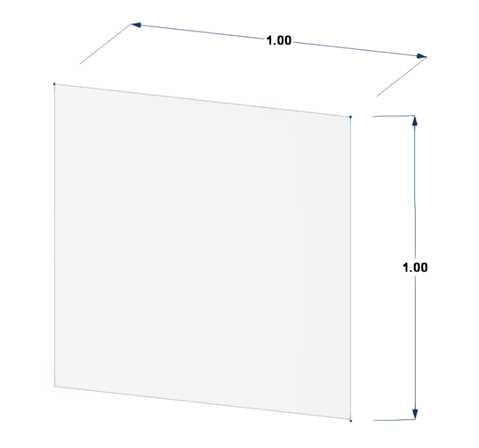
Wymiary przykładu przedstawiono na Rysunku 1, a założenie wejściowe zilustrowano w Tabeli 1:
Tabela 1: Dane wejściowe przykładu weryfikacji 2D kwadratowej płaszczyzny
| Model | 2D kwadratowa płaszczyzna |
|---|---|
| Wymiar | a = 1 m |
| Podstawowa prędkość wiatru | V = 30 m/s |
| Gęstość powietrza | ρ = 1.225 kg/m³ |
| Rozwiązanie | Oparte na ciśnieniu |
| Model turbulencji | Steady k-ω SST |
| Kategoria terenu | 2 |
| Typ profilu prędkości wiatru w RFEM | Szczytowy |
| Algorytm numeryczny | Algorytm SIMPLE |
| Dyskretyzacja | Drugi rząd |
| Ciśnienie resztkowe | 10⁻⁴ |
| Lepkość kinematyczna | ν = 1.5 × 10⁻⁵ |
W tym przykładzie porównamy wartości siły wiatru pomiędzy EN 1991-1-4 a RWIND. Wzór na siłę wiatru w sekcji Eurokodu 5.3 jest zdefiniowany:
|
cscd |
Structural factor |
|
cf |
Force coefficient for the structure or structural element |
|
qp(ze ) |
Peak velocity pressure at reference height ze |
|
Aref |
Reference area of the structure or structural element |
Współczynniki siły (d=b=1 → Cf,0=2.10) prostokątnych przekrojów o ostrych narożach i bez przepływu końcowego można uzyskać na Rysunku 7.23 w EN 1991-1-4, a współczynnik redukcji (ψr) dla przekroju kwadratowego z zaokrąglonymi narożami (r/b=0 → ψ r=1) można uzyskać z Rysunku 7.24 w EN 1991-1-4. Wartości orientacyjne współczynnika efektu końcowego ψλ=0.63 jako funkcji współczynnika wypełnienia φ=1 w porównaniu do smukłości λ=2 można uzyskać na Rysunku 7.36 w EN 1991-1-4.
Współczynnik siły cf elementów strukturalnych prostokątnego przekroju z wiatrem wiejącym normalnie na płaską powierzchnię należy określić według Wyrażenia (7.9) w EN 1991-1-4:
|
cf,0 |
The force coefficient of rectangular sections with sharp corners and without free-end flow |
|
ψr |
The reduction factor for square sections with rounded corners |
|
ψλ |
The end-effect factor for elements with free-end flow |
- Średnia prędkość wiatru
Średnia prędkość wiatru vm (ze) na wysokości odniesienia z_e zależy od szorstkości terenu, orografii terenu i podstawowej prędkości wiatru vb. Jest ona określana za pomocą równania EN1991-1-4 (4.3):
- Turbulencja wiatru
Intensywność turbulencji Iv (ze) na wysokości odniesienia ze jest zdefiniowana jako odchylenie standardowe turbulencji podzielone przez średnią prędkość wiatru. Jest obliczana zgodnie z Równaniem 4.7 EN1991-1-4. Dla badanego przypadku ze mniejsze niż zmin:
- Podstawowe ciśnienie prędkości
Podstawowe ciśnienie prędkości q_b odpowiada ciśnieniu wiatru określonemu przy podstawowej prędkości wiatru vb. Podstawowe ciśnienie prędkości jest obliczane zgodnie z podstawową zależnością określoną w EN1991 -14 §4.5(1):
gdzie ρ jest gęstością powietrza zgodnie z EN1991-1-4 §4.5(1). W tym obliczeniu brana pod uwagę jest następująca wartość ρ=1.225 kg/m3.
- Szczytowe ciśnienie prędkości
Szczytowe ciśnienie prędkości qp (ze) na wysokości odniesienia ze obejmuje średnie i krótkoterminowe fluktuacje prędkości. Jest określane zgodnie z Równaniem 4.8 EN1991-1-4:
Następnie można obliczyć siłę wiatru:
Obraz 2 pokazuje badanie wrażliwości siatki w RWIND dla płyty 2D. W miarę wzrostu gęstości siatki od 10% do 40%, współczynnik siły Cf maleje i stabilizuje się na poziomie 1.23 od 30% wzwyż, co wskazuje na niezależne od siatki wyniki i zapewnia dokładność symulacji bez zbędnego refinamentu.
Badanie siatki obliczeniowej musi być również przeprowadzone według poniższego linku:
WTG-Merkblatt M3 dostarcza dwie kluczowe metody walidacji wyników symulacji. Metoda Hit Rate ocenia, ile z symulowanych wartości Pi poprawnie zgadza się z wartościami odniesienia Oi w ramach zdefiniowanej tolerancji, wykorzystując podejście binarnej klasyfikacji (trafienie lub niepowodzenie). Podejście to ocenia niezawodność symulacji poprzez obliczenie wskaźnika trafień q, podobnie jak funkcje ufności stosowane w teorii niezawodności. Natomiast metoda Znormalizowanego Średniego Kwadratu Błędu (e2) oferuje bardziej szczegółową ocenę dokładności poprzez kwantyfikację średniego kwadratowego odchylenia pomiędzy wartościami symulowanymi a odniesienia, znormalizowaną do uwzględnienia różnic w skali. Razem te metody dostarczają zarówno jakościowych, jak i ilościowych miar walidacji symulacji.
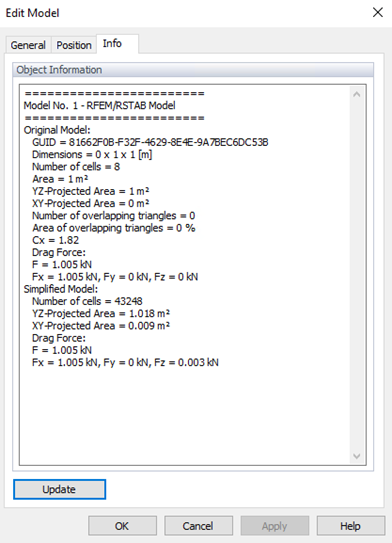
Wyniki w RWIND i Porównanie z Eurokodem
W RWIND wyniki całkowitych sił (w Rysunkach 3 i 4) są dostępne w karcie Informacje podczas edycji modelu. Różnica pomiędzy RWIND a Eurokodem wynosi około Wrel = 2.45% (mniej niż wspomniane kryteria w WTG); wówczas współczynnik trafień może być uzyskany jako q=100%, co pokazuje dobrą zgodność. Niski znormalizowany średni kwadratowy błąd e2=0.0005 potwierdza silną zgodność pomiędzy symulacją a pomiarami, efektywnie spełniając standardy walidacji.
Oto model 3D płyty 2D: