Descrizione
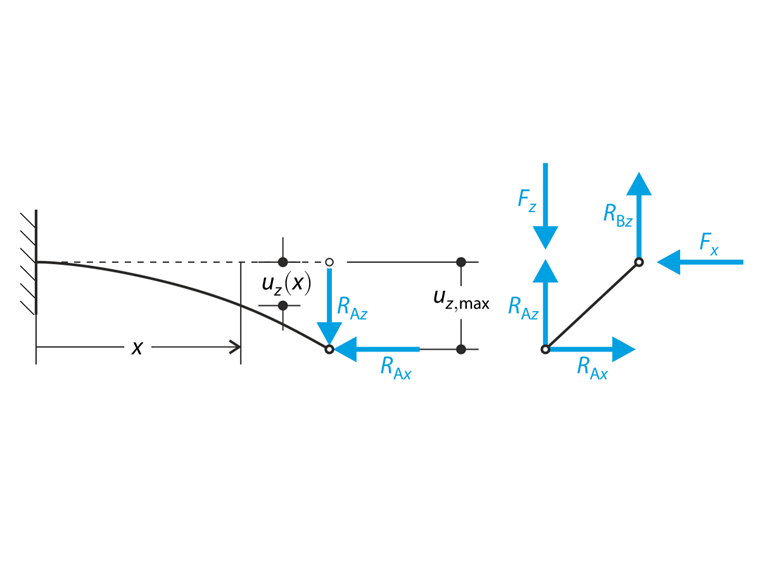
Una struttura realizzata con profilo a I è completamente fissata all'estremità sinistra e incorporata nel supporto scorrevole all'estremità destra. La struttura è costituita da due segmenti secondo il seguente . Il peso proprio è trascurato in questo esempio. Determina l'inflessione massima della struttura uz,max, il momento flettente My sull'estremità fissa, la rotazione φ2,y del segmento 2 e la forza di reazione RBz mediante l'analisi geometricamente lineare e del secondo ordine analisi. L'esempio di verifica si basa sull'esempio introdotto da Gensichen e Lumpe (vedere il riferimento).
| Materiale | Acciaio | Modulo di elasticità | E | 210000,000 | MPa |
| deformazione trasversale | ν | 0,300 | - | ||
| Geometria | Struttura | Lunghezza del segmento 1 | L1 | 6,000 | m |
| Lunghezza del segmento 2 | L2 | 1,200 | m | ||
| Sezione trasversale | Altezza | h | 400,000 | mm | |
| Larghezza | b | 180,000 | mm | ||
| Spessore dell'anima | s | 10,000 | mm | ||
| spessore dell'ala | t | 14,000 | mm | ||
| Carico | forza assiale | Fx | 100,000 | kN | |
| Forza trasversale | Fz | 0,500 | kN | ||
Soluzione analitica
Geometricamente lineare analisi
All'inizio viene eseguita l'analisi geometricamente lineare. In questo caso, la forza assiale Fx non viene presa in considerazione. Il problema può essere quindi risolto anche con uno sbalzo della lunghezza L1 caricato solo dalla forza trasversale Fz. L'inflessione massima uz,max può essere calcolata utilizzando l'integrale di Mohr's e risulta nell'espressione:
| F<sub>y</sub> | Momento quadratico della sezione trasversale rispetto all'asse y |
Il momento flettente sull'estremità fissa può essere calcolato secondo la seguente formula:
La rotazione del segmento 2 φ2,y è calcolata dalla condizione geometrica come segue:
La forza di reazione nel giunto scorrevole RBz considerando l'effetto zero della forza assiale Fx può essere ottenuta dal diagramma del corpo libero mostrato nel seguente del corpo libero.
Analisi del secondo ordine
A causa dell'effetto non trascurabile della forza assiale Fx, l'analisi del secondo ordine dovrebbe essere considerata. Pertanto, la forza assiale Fx viene presa in considerazione e produce un altro contributo al momento flettente. Il problema può essere descritto dal diagramma a corpo libero dei segmenti secondo lo a corpo libero. Le forze di reazione sconosciute possono essere ottenute dalle equazioni di equilibrio e quindi può essere scritta la formula del momento flettente.
La soluzione può essere trovata con l'equazione differenziale di Eulero-Bernoulli.
Considerando le condizioni al contorno, è possibile trovare la soluzione dell'equazione differenziale e calcolare l'inflessione massima della struttura.
Il momento flettente sull'estremità fissa può essere calcolato secondo la seguente formula:
La rotazione del segmento 2 φ2,y è calcolata dalla condizione geometrica come segue:
La forza di reazione nel giunto scorrevole RBz risulta:
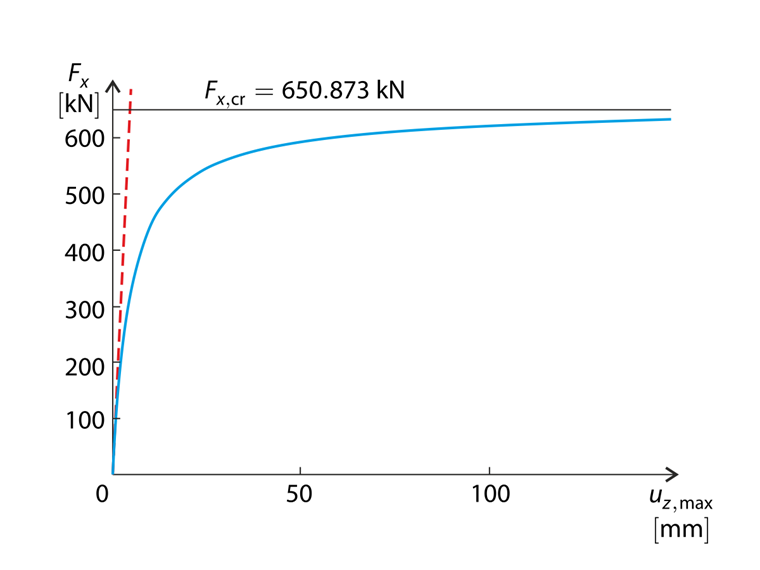
È ovvio che l'influenza della forza assiale Fx è considerevole. L'inflessione totale della struttura sotto il carico prescritto nel caso dell'analisi del secondo ordine è di circa il 18 % maggiore rispetto al caso dell'analisi geometricamente lineare. Il confronto tra l'analisi geometricamente lineare e l'analisi del secondo ordine è mostrato nel graph, considerando il rapporto tra le forze di carico Fz = Fx/200. È ovvio che la differenza tra queste analisi è più notevole quando il carico è maggiore. La soluzione dell'analisi del secondo ordine si sta avvicinando all'asintoto orizzontale. La soluzione numerica fornisce il valore dell'asintoto orizzontale Fx,cr = 650,873 kN.
Impostazioni di RFEM e RSTAB
- Modellato in RFEM 5.05 e RSTAB 8.05 e RFEM 6.01, RSTAB 9.01
- Il numero di elementi è 2 (un elemento per asta)
- Il numero di incrementi è 5
- Viene utilizzato il modello di materiale elastico lineare isotropo
- La struttura è modellata utilizzando le aste
- La rigidezza a taglio delle aste è trascurata
Risultati
| Analisi geometricamente lineare | Soluzione analitica | RFEM 6 | Rapporto | RSTAB 9 | Rapporto |
| uz,max [mm] | 0,743 | 0,743 | 1,000 | 0,743 | 1,000 |
| My (0) [kNm] | 3,000 | 3,000 | 1,000 | 3,000 | 1,000 |
| φ2,y [mrad] | 0,619 | 0,619 | 1,000 | 0,619 | 1,000 |
| [SCHOOL.SCHOOLORINSTITUTION]Bz [kN] | 0,000 | 0,000 | - | 0,000 | - |
| Analisi geometricamente lineare | Soluzione analitica | RFEM 5 | Rapporto | RSTAB 8 | Rapporto |
| uz,max [mm] | 0,743 | 0,743 | 1,000 | 0,743 | 1,000 |
| My (0) [kNm] | 3,000 | 3,000 | 1,000 | 3,000 | 1,000 |
| φ2,y [mrad] | 0,619 | 0,619 | 1,000 | 0,619 | 1,000 |
| [SCHOOL.SCHOOLORINSTITUTION]Bz [kN] | 0,000 | 0,000 | - | 0,000 | - |
| Analisi del secondo ordine | Soluzione analitica | RFEM 6 | Rapporto | RSTAB 9 | Rapporto |
| uz,max [mm] | 0,878 | 0,878 | 1,000 | 0,878 | 1,000 |
| My (0) [kNm] | 3,527 | 3,527 | 1,000 | 3,527 | 1,000 |
| φ2,y [mrad] | 0,732 | 0,732 | 1,000 | 0,732 | 1,000 |
| [SCHOOL.SCHOOLORINSTITUTION]Bz [kN] | -0,073 | -0,073 | 1,000 | -0,073 | 1,000 |
| Analisi del secondo ordine | Soluzione analitica | RFEM 5 | Rapporto | RSTAB 8 | Rapporto |
| uz,max [mm] | 0,878 | 0,878 | 1,000 | 0,878 | 1,000 |
| My (0) [kNm] | 3,527 | 3,527 | 1,000 | 3,527 | 1,000 |
| φ2,y [mrad] | 0,732 | 0,732 | 1,000 | 0,732 | 1,000 |
| [SCHOOL.SCHOOLORINSTITUTION]Bz [kN] | -0,073 | -0,073 | 1,000 | -0,073 | 1,000 |
,_LC1__LI.jpg?mw=760&hash=dc8e32cc15e1bd8d6d238956c9f1c615aa29a734)
,_LC1__LI.jpg?mw=350&hash=6ed041c2883863d5ca78996c15f07c7d24cb0baf)
,_LC1__LI.jpg?mw=350&hash=6ed041c2883863d5ca78996c15f07c7d24cb0baf)
,_LC1__LI.jpg?mw=350&hash=6ed041c2883863d5ca78996c15f07c7d24cb0baf)
,_LC1__LI.jpg?mw=350&hash=6ed041c2883863d5ca78996c15f07c7d24cb0baf)
