Neste capítulo, será explicado como as forças de tração nos estribos horizontais individuais do casquilho são derivadas das forças horizontais aplicadas. Será demonstrado como as forças são compostas de tração direta e do momento fletor na parede do casquilho, sendo distribuídas entre os diferentes grupos de estribos por meio de mecanismos de biela de compressão.
Forças Horizontais nas Paredes do Casquilho
No primeiro passo do dimensionamento, é investigada a distribuição das forças horizontais nas paredes do casquilho. Dependendo se a superfície de contato entre o suporte e o casquilho é áspera ou lisa, diferentes porções de forças horizontais podem ser transmitidas. As forças horizontais resultantes formam a base para a posterior determinação das forças de tração nos estribos.
O dimensionamento é feito apenas para a força horizontal superior, mesmo que a inferior geralmente seja maior, pelos seguintes motivos:
- Na área inferior, a parede frontal é parcialmente engastada devido à armadura vertical e à ligação com a placa de fundação. Portanto, a força horizontal não atua da mesma forma que na área superior.
- O casquilho é frequentemente feito mais espesso na parte inferior, o que aumenta a capacidade de carga e torna a maior força inferior menos crítica.
- O dimensionamento do concreto é feito para uma largura parcial específica (cerca de 1/3 da altura da parede), independentemente da altura total, o que proporciona segurança adicional.
Para uma fundação com casquilho com superfícies internas ásperas, a força horizontal superior é:
|
My |
Momento fletor de cálculo |
|
d |
Profundidade de embutimento do pilar |
|
Hx |
Força horizontal de dimensionamento sem cargas adicionais de fundações |
Para uma fundação com casquilho com superfícies internas lisas, a força horizontal superior é:
Verificação do Concreto da Parede do Casquilho Solicitada por Flexão
A verificação é feita exemplificando a parede do casquilho na direção y, que é solicitada por uma força horizontal superior Ht,x na direção x. Assim, a flexão ocorre em torno do eixo y. A força horizontal superior Ht,x pode ser dividida de forma que metade atue nos pontos quarteirões ao longo da extensão longitudinal do suporte na direção y.
Considerando apenas o canto superior direito isoladamente, este deve estar em equilíbrio de forças:
O momento em torno do ponto P é calculado da seguinte forma:
O momento fletor de dimensionamento MEd deve ser equilibrado por um momento oposto. Este surge da força de compressão do concreto no lado comprimido da parede do casquilho na direção y com o braço de alavanca z em relação ao ponto de rotação P:
Para determinar a compressão necessária do concreto, prosseguem-se da seguinte forma:
- Assume-se que a tensão do concreto é distribuída uniformemente sobre a zona de compressão.
- Começando com uma deformação do concreto de 0,0 ‰, esta é aumentada gradualmente até que o momento interno resultante corresponda ao momento de dimensionamento MEd.
- Simultaneamente, assume-se que o aço no lado externo da parede do casquilho já atingiu sua deformação máxima.
Assim que o momento interno calculado for maior que o momento de dimensionamento MEd, a iteração é concluída. A parede do casquilho é então verificada para flexão e a área de armadura necessária dos estribos horizontais no casquilho devido à flexão de Ht,x Asw,h,erf (MEd|Ht,x) é determinada.
Armadura Horizontal Externa
O estribo externo em todos os lados é solicitado por duas solicitações diferentes:
- Devido à flexão da parede perpendicular à força horizontal considerada
- Devido à tração da parede que se estende paralelamente à força horizontal considerada
Na imagem, a armadura resultante devido a Ht,x e a correspondente Ht,y estão representadas.
| Armadura | Denominação |
|---|---|
| Asw,h,out,erf(MEdHt,x) | Área de armadura necessária dos estribos horizontais externos no casquilho devido à flexão de Ht,x |
| Asw,h,erf(Ht,x) | Área de armadura necessária dos estribos horizontais no casquilho devido à força de tração na direção x |
| Asw,h,out,erf(MEdHt,y) | Área de armadura necessária dos estribos horizontais externos no casquilho devido à flexão de Ht,y |
| Asw,h,erf(Ht,y) | Área de armadura necessária dos estribos horizontais no casquilho devido à força de tração na direção y |
A solicitação máxima de tração dos estribos resulta da soma das forças de tração devido à flexão e à força de tração axial. A armadura necessária é determinada como segue:
Armadura Horizontal na Direção y
Neste estribo, apenas as forças horizontais na direção x causam forças de tração. A força horizontal Ht,y não causa força de tração aqui por dois motivos:
- Não há força de tração devido à flexão na direção y: O ramo do estribo na direção x está dentro da zona de compressão da parede solicitada por Ht,y. Aqui, o estribo atua mais como armadura de compressão, que no entanto é desconsiderada.
- Nenhum componente de tração devido a ramos do estribo paralelos: Os ramos do estribo que se estendem paralelamente à força horizontal Ht,y transferem suas forças por meio de bielas de compressão diagonais para a parte externa do casquilho. Lá, a força vertical é introduzida nos ramos verticais do estribo. Como o ramo vertical do estribo externo em y está acima deste ponto de introdução, não há componente vertical da biela de compressão neste estribo.
Armadura Horizontal na Direção x
Analogamente à armadura na direção y, apenas as forças horizontais que atuam perpendicularmente à direção do ramo do estribo causam uma força de tração no estribo.
Derivação das Forças de Tração nos Estribos a partir das Forças Horizontais
Ainda deve ser explicado como as forças de tração nos estribos, que foram então superadas para a força de tração determinante, de fato surgiram a partir das forças horizontais. Isso será exemplificado para a força horizontal Ht,x.
Divisão da Força Horizontal nos Estribos
A força horizontal Ht,x é distribuída uniformemente nos quatro ramos do estribo que atuam paralelamente à força. Cada um desses ramos, portanto, suportam um quarto da força total:
A armadura necessária é então:
Efeito de Flexão na Parede do Casquilho
Adicionalmente, Ht,x causa flexão na parede do casquilho na direção y. Durante o dimensionamento do concreto, a força de compressão resultante no concreto foi determinada. Por razões de equilíbrio, essa força de compressão no concreto deve ser compensada por uma força de tração correspondente nos estribos externos.
Componente de Tração nos Estribos Externos:
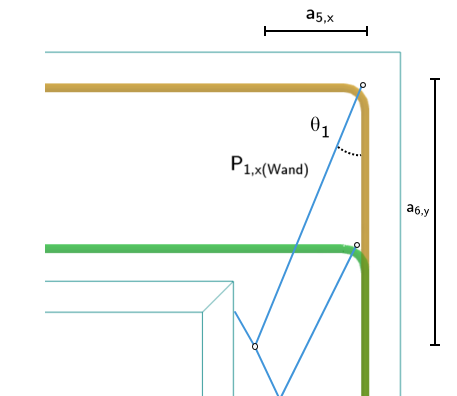
Essa força de tração de flexão não é distribuída uniformemente entre ambos os estribos horizontais, mas segue a mecânica da biela de compressão. As bielas se espalham sob um ângulo θ1.
Para obter o componente de tração que surge da flexão na parede do casquilho, sugere-se os seguintes passos:
Ângulo de propagação de carga dentro da parede do casquilho:
com:
|
dx(wall) |
Altura de utilização estrutural na parede na direção x |
|
kx(wall) |
Relação para braço de alavanca de forças internas |
|
xx(parede) |
Altura da zona de pressão utilizada para o braço de alavanca das forças internas devido a dimensionamento |
|
db,y |
Dimensão de encaixe na direção y |
|
cy |
Dimensão de pilare na direção y |
|
c(k) |
Recobrimento de betão existente na fundação de encaixe |
|
ds,h |
Diâmetro dos estribos horizontais no encaixe |
Força de compressão proporcional em estribos externos devido à flexão da parede do casquilho:
Força de tração proporcional em estribos externos devido à flexão da parede do casquilho:
A área de armadura necessária dos estribos horizontais externos no casquilho devido à flexão de Ht,x é então:
A área de armadura necessária dos estribos horizontais na direção y no casquilho devido à flexão de Ht,x corresponde então à porção restante da área de armadura total necessária após a dedução da armadura dos estribos externos Asw,h,out,erf (MEd|Ht,x):