53695x

001469

Sonja von Bloh, M.Sc.

2024-01-18

Расчет угловых сварных швов по норме EN 1993-1-8

Угловой сварной шов является наиболее распространенным типом сварного шва в стальных строительных конструкциях. По норме EN 1993‑1‑8, 4.3.2.1 (1) [1], можно использовать угловые швы для соединения конструктивных элементов, у которых поверхности проплавления образуют угол от 60° до 120°.

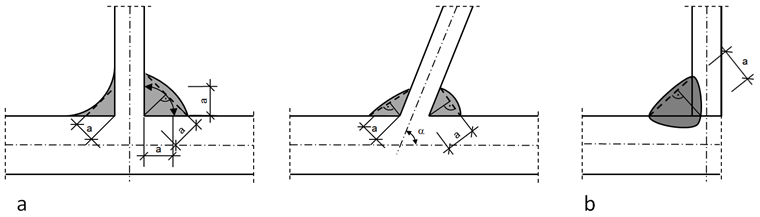
Эффективная толщина шва a углового шва обычно принимается как высота вписываемого (равнобедренного или неравнобедренного) треугольника, измеренная до теоретической точки корня, см. рисунок 01.

Толщина углового шва a для нормального (a) и глубокого (b)

Толщина углового шва a для различного проплавления. Толщина углового шва a для нормального проникновения b Толщина углового шва для глубокого проплавления

Носимость угловых швов

Носимость угловых швов согласно 1993-1-8 [1] обычно определяется с использованием направленного метода или упрощенного метода. Ниже приведено описание направленного метода.

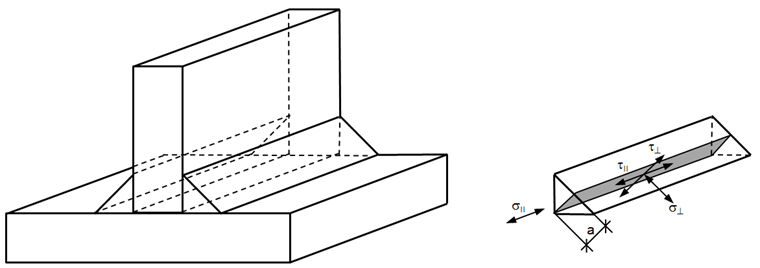
Предполагается, что прикладываемое напряжение равномерно распределено по сечению шва и приводит, как показано на рисунке 02, к следующим нормальным и сдвиговым напряжениям:

σ⊥ нормальное напряжение, перпендикулярное оси сварного шва σ|| нормальное напряжение, параллельное оси сварного шва τ⊥ сдвиговое напряжение (в плоскости поверхности углового шва) перпендикулярно оси сварного шва τ|| сдвиговое напряжение (в плоскости поверхности углового шва) параллельно оси сварного шва

Напряжения при сварке в эффективном сечении углового шва

При определении допустимой нагрузки углового шва нормальные напряжения σ||, параллельные оси сварного шва, игнорируются.

Носимость углового шва считается достаточной, если выполнены следующие условия:

\begin{array}{l} \sqrt{σ_{⊥}^{2} + 3 \cdot (τ_{⊥}^{2} + τ_{| |}^{2})} \leq \frac{f_{u}}{β_{w} \cdot γ_{M 2}} \\ σ_{⊥} \leq 0, 9 \cdot \frac{f_{u}}{γ_{M 2}} \end{array}

Формула 1

Где fu - предел прочности на растяжение слабейшего из соединяемых элементов, βw - коэффициент корреляции (см. EN 1993-1-8, таблица 4.1), γM2 - частный коэффициент безопасности для допустимой нагрузки сварных швов.

Пример

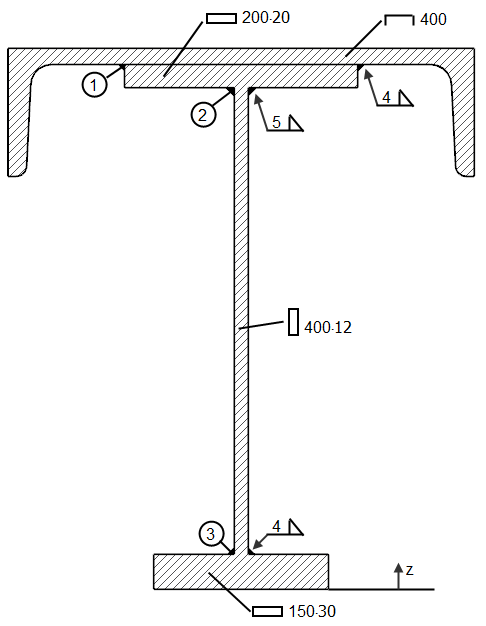
Проверка угловых швов балки, показанной на рисунке 03, из [2].

Материал: S235, fu = 36,0 кН/см², βw = 0,8 Сечения: Vz = 350 кН

Балка

Центр тяжести

z_{S} = \frac{Σ (A_{i} \cdot z_{Si})}{{ΣA}_{i}} = \frac{91, 48 \cdot 43, 72 40, 00 \cdot 44, 00 48, 00 \cdot 23, 00 45, 00 \cdot 1, 50}{224, 48} = 30, 88 cm

Формула 2

Момент инерции Относительно главной оси момент инерции составляет:

\begin{array}{l} I_{y} = \sum (I_{yi} + A_{i} \cdot z_{si}^{2}) - \frac{{(\sum A_{i} \cdot z_{Si})}^{2}}{{ΣA}_{i}} = \\ = 850, 88 \frac{20, 00 \cdot 2, 00 ³}{12} \frac{1, 20 \cdot 40, 00 ³}{12} \frac{15, 00 \cdot 3, 00 ³}{12} 91, 48 \cdot 43, 72 ² 40, 00 \cdot 44, 00 ² 48, 00 \cdot 23, 00 ² 45, 00 \cdot 1, 50 ² - \\ - \frac{(91, 48 \cdot 43, 72 40, 00 \cdot 44, 00 48, 00 \cdot 23, 00 45, 00 \cdot 1, 50) ²}{224, 48} = \\ = 71.095 {cm}^{4} \end{array}

Формула 3

Статические моменты Относительно главной оси статические моменты для частей сечения, подключенных с помощью швов➀, ➁ и ➂, рассчитываются: Sy,1 = A1 ∙ (zS,1 - zS) = 91,48 ∙ (43,72- 30,88) = 1.175 см³ Sy,2 = Sy,1 + A2 ∙ (zS,2 - zS)= 1175 + 40,00 ∙ (44,00 - 30,88) = 1.700 см³ Sy,3 = A3 ∙ (zS - zS,3) = 45,00 ∙ (30,88- 1,50) = 1.322 см³

Проверка сварных швов

\begin{array}{l} τ_{| |, Vz, i} = \frac{- V_{z} \cdot S_{y, i}}{I_{y} \cdot {Σa}_{w, i}} \leq \frac{f_{u}}{\sqrt{3} \cdot β_{w} \cdot γ_{M 2}} = \frac{36, 0}{\sqrt{3} \cdot 0, 8 \cdot 1, 25} = 20, 78 kN / cm ² \\ τ_{| |, Vz, 1} = \frac{- 350 \cdot 1.175}{71.095 \cdot 2 \cdot 0, 4} = - 7, 23 kN / cm ² < 20, 78 kN / cm ² \\ τ_{| |, Vz, 2} = \frac{- 350 \cdot 1.700}{71.095 \cdot 2 \cdot 0, 5} = - 8, 37 kN / cm ² < 20, 78 kN / cm ² \\ τ_{| |, Vz, 3} = \frac{- 350 \cdot 1.322}{71.095 \cdot 2 \cdot 0, 4} = - 8, 13 kN / cm ² < 20, 78 kN / cm ² \end{array}

Формула 4

DUENQ

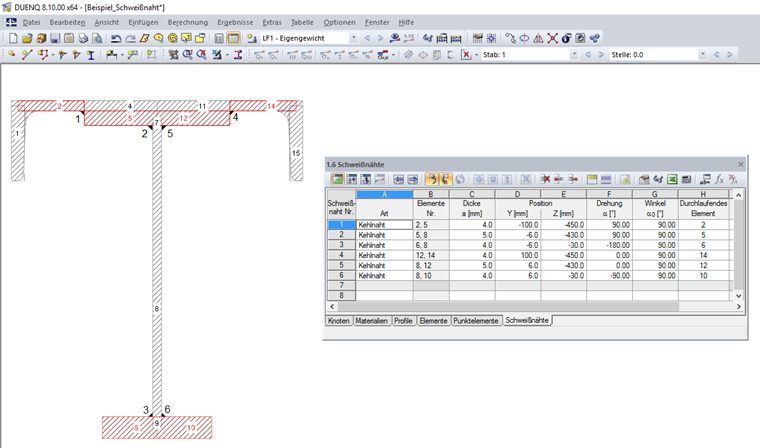
В DUENQ можно рассчитать сдвиговое напряжение (в плоскости поверхности углового шва) параллельно оси сварного шва τ|| на угловых швах и проверить их носимость. При моделировании важно, чтобы сварной шов был подключен к краям двух элементов. Один из этих элементов может быть нулевым элементом.

В столбце H "Проходящий элемент" таблицы 1.6 Сварные швы могут быть определены проходящие элементы. На этих элементах не рассчитываются напряжения сварного шва. Если в столбце H не указан элемент, то напряжения сварного шва определяются на всех элементах, к которым подключен сварной шов. Эти элементы можно найти в столбце B "Элементы №".

На рисунке 04 показано определение сварного шва для рассматриваемого примера.

Таблица 1.6 Сварные швы

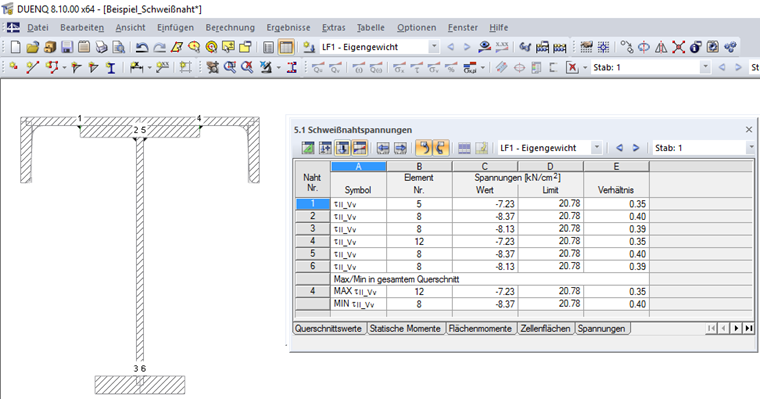
Таблица 5.1 Напряжения сварных швов выводит напряжения τ|| для швов, определенных в таблице 1.6 Сварные швы. На рисунке 05 показаны напряжения сварных швов для рассматриваемого примера.

Таблица 5.1 Напряжения при сварке

Литература [1] Еврокод 3: Проектирование стальных конструкций - Часть 1-8: Проектирование соединений; EN 1993-1-8:2005 + AC:2009 [2] Петерсен, C.: Стальные конструкции, 4-е издание. Висбаден: Springer Vieweg, 2013

Автор

Г-жа фон Бло оказывает техническую поддержку нашим клиентам и отвечает за разработку программы SHAPE‑THIN, а также стальных и алюминиевых конструкций.

Ссылки

Программы для расчета характеристик сечений

Ссылки

Европейские рекомендации по расчёту простых соединений в стальных конструкциях. ECCS - European Convention for Constructional Steelwork, Mem Martins, edition = 1. 2009.

Скачивания

Файл модели в программе SHAPE-THIN

364 KB

;