53506x

001469

Sonja von Bloh, M.Sc.

2024-01-18

Projektowanie spoin pachwinowych wg EN 1993-1-8

Spoina pachwinowa jest zdecydowanie najczęściej spotykaną formą spoiny w budownictwie stalowym. Zgodnie z EN 1993-1-8, 4.3.2.1 (1) [1] spoiny pachwinowe mogą być stosowane do łączenia elementów konstrukcyjnych, jeśli zbocza tworzą kąt otwarcia od 60° do 120°.

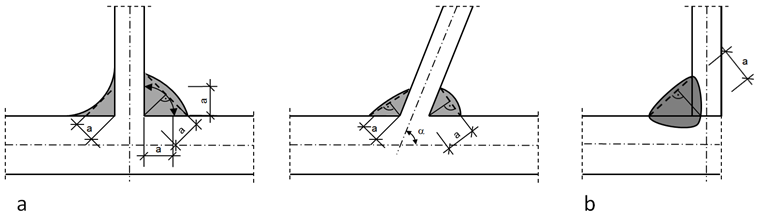
Efektywna grubość spoiny a dla spoiny pachwinowej jest zazwyczaj uważana za wysokość trójkąta wpisanego (równoramiennego lub nierównoramiennego), mierzona do teoretycznego punktu korzenia, patrz rysunek 01.

Grubość spoiny pachwinowej a dla normalnego przetopu (a) i dla głębokiego przetopu (b)

Grubość spoiny pachwinowej a dla innego przetopu. Grubość spoiny pachwinowej a dla normalnej penetracji b Grubość spoiny pachwinowej dla głębokiej penetracji

Nośność spoin pachwinowych

Nośność spoin pachwinowych określa się zgodnie z normą 1993-1-8 [1] zwykle metodą kierunkową lub metodą uproszczoną. Metodę kierunkową przedstawiono poniżej.

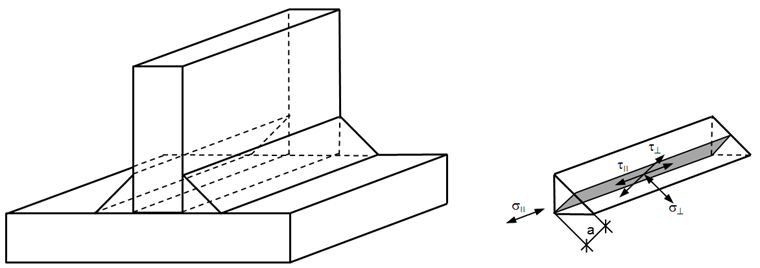
Zakłada się, że działające naprężenie rozkłada się równomiernie na przekrój poprzeczny spoiny i prowadzi, jak pokazano na rysunku 02, do następujących naprężeń normalnych i ścinających:

σ⊥ naprężenie normalne prostopadłe do osi spoiny, σ|| naprężenie normalne równoległe do osi spoiny, τ⊥ naprężenie ścinające (w płaszczyźnie powierzchni spoiny pachwinowej) prostopadłe do osi spoiny, τ|| naprężenie ścinające (w płaszczyźnie powierzchni spoiny pachwinowej) równoległe do osi spoiny

Naprężenia spoiny w efektywnym przekroju spoiny pachwinowej

Przy określaniu nośności spoiny pachwinowej pomija się naprężenia normalne σ|| równoległe do osi spoiny.

Nośność spoiny pachwinowej jest wystarczająca, jeśli spełnione są następujące warunki:

\begin{array}{l} \sqrt{σ_{⊥}^{2} + 3 \cdot (τ_{⊥}^{2} + τ_{| |}^{2})} \leq \frac{f_{u}}{β_{w} \cdot γ_{M 2}} \\ σ_{⊥} \leq 0, 9 \cdot \frac{f_{u}}{γ_{M 2}} \end{array}

Wzór 1

Gdzie: fu to wytrzymałość na rozciąganie słabszego z przyłączonych elementów, βw to współczynnik korelacji (patrz EN 1993-1-8, tabela 4.1), γM2 to częściowy współczynnik bezpieczeństwa dla nośności spoin.

Przykład

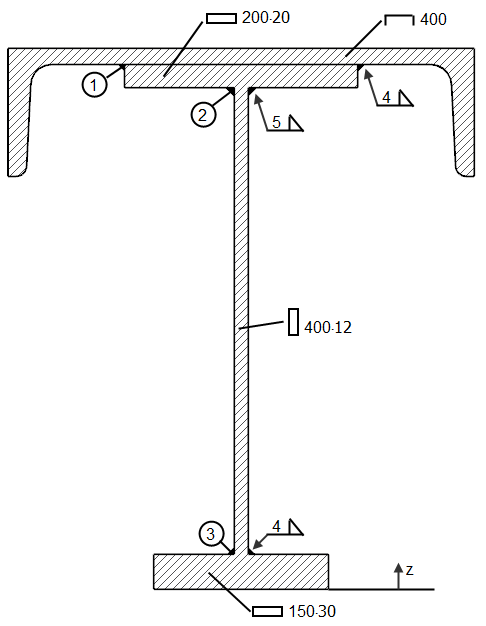
Weryfikacja spoin pachwinowych belki przedstawionej na rysunku 03 z [2].

Materiał: S235, fu = 36,0 kN/cm², βw = 0,8 Wielkości przekrojowe: Vz = 350 kN

złącze kratownica-podciąg

Środek ciężkości

z_{S} = \frac{Σ (A_{i} \cdot z_{Si})}{{ΣA}_{i}} = \frac{91, 48 \cdot 43, 72 40, 00 \cdot 44, 00 48, 00 \cdot 23, 00 45, 00 \cdot 1, 50}{224, 48} = 30, 88 cm

Wzór 2

Moment bezwładności W odniesieniu do osi ciężkości moment bezwładności wynosi:

\begin{array}{l} I_{y} = \sum (I_{yi} + A_{i} \cdot z_{si}^{2}) - \frac{{(\sum A_{i} \cdot z_{Si})}^{2}}{{ΣA}_{i}} = \\ = 850, 88 \frac{20, 00 \cdot 2, 00 ³}{12} \frac{1, 20 \cdot 40, 00 ³}{12} \frac{15, 00 \cdot 3, 00 ³}{12} 91, 48 \cdot 43, 72 ² 40, 00 \cdot 44, 00 ² 48, 00 \cdot 23, 00 ² 45, 00 \cdot 1, 50 ² - \\ - \frac{(91, 48 \cdot 43, 72 40, 00 \cdot 44, 00 48, 00 \cdot 23, 00 45, 00 \cdot 1, 50) ²}{224, 48} = \\ = 71.095 {cm}^{4} \end{array}

Wzór 3

Momenty statyczne W odniesieniu do osi ciężkości oblicza się momenty statyczne dla części przekroju przyłączonych za pomocą spoin ➀, ➁ i ➂: Sy,1 = A1 ∙ (zS,1 - zS) = 91,48 ∙ (43,72 - 30,88) = 1.175 cm³ Sy,2 = Sy,1 + A2 ∙ (zS,2 - zS) = 1175 + 40,00 ∙ (44,00 - 30,88) = 1.700 cm³ Sy,3 = A3 ∙ (zS - zS,3) = 45,00 ∙ (30,88 - 1,50) = 1.322 cm³

Weryfikacja spoin

\begin{array}{l} τ_{| |, Vz, i} = \frac{- V_{z} \cdot S_{y, i}}{I_{y} \cdot {Σa}_{w, i}} \leq \frac{f_{u}}{\sqrt{3} \cdot β_{w} \cdot γ_{M 2}} = \frac{36, 0}{\sqrt{3} \cdot 0, 8 \cdot 1, 25} = 20, 78 kN / cm ² \\ τ_{| |, Vz, 1} = \frac{- 350 \cdot 1.175}{71.095 \cdot 2 \cdot 0, 4} = - 7, 23 kN / cm ² < 20, 78 kN / cm ² \\ τ_{| |, Vz, 2} = \frac{- 350 \cdot 1.700}{71.095 \cdot 2 \cdot 0, 5} = - 8, 37 kN / cm ² < 20, 78 kN / cm ² \\ τ_{| |, Vz, 3} = \frac{- 350 \cdot 1.322}{71.095 \cdot 2 \cdot 0, 4} = - 8, 13 kN / cm ² < 20, 78 kN / cm ² \end{array}

Wzór 4

DUENQ

W DUENQ można obliczyć naprężenie ścinające (w płaszczyźnie powierzchni spoiny pachwinowej) równoległe do osi spoiny τ|| na spoinach pachwinowych i zweryfikować nośność. Podczas modelowania należy zwrócić uwagę, aby spoina była przyłączona do krawędzi dwóch elementów. Jeden z tych elementów może być również elementem zerowym.

W kolumnie H "Element przekrojony" tabeli 1.6 Spojenia można określić elementy przekrojone. Na tych elementach nie są obliczane naprężenia spoin. Jeśli w kolumnie H nie podano żadnego elementu, to naprężenia spoin są określane na wszystkich elementach, do których przyłączona jest spoina. Elementy te można znaleźć w kolumnie B "Nr elementu".

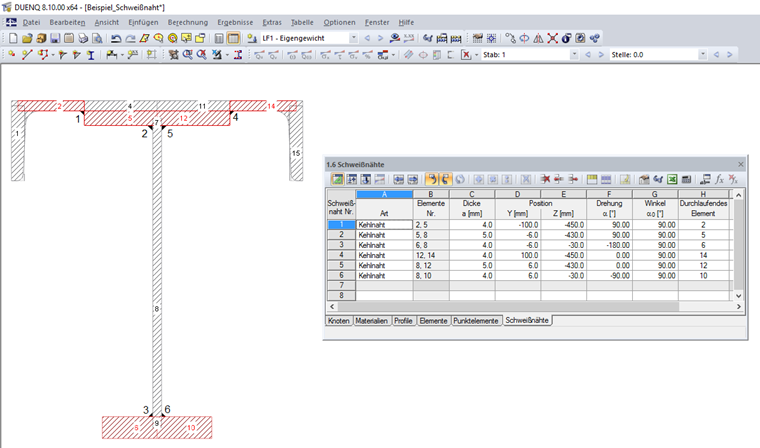
Na rysunku 04 przedstawiono definicję spoiny dla przykładu omawianego.

Tabela 1.6 Spoiny

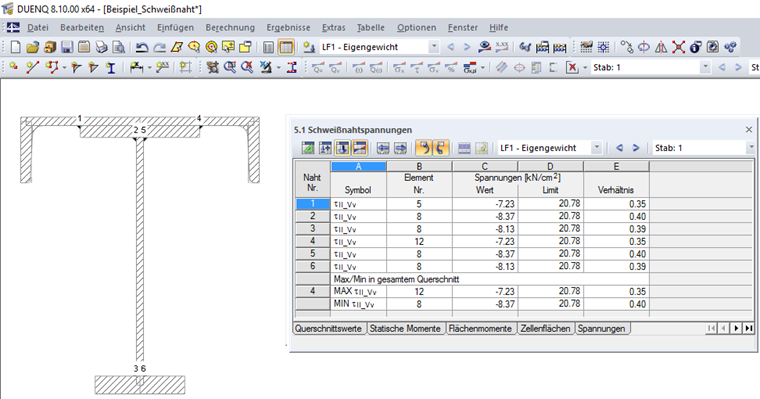
Tabela 5.1 Naprężenia spoin dostarcza wartości naprężeń τ|| dla spoin zdefiniowanych w tabeli 1.6 Spojenia. Rysunek 05 pokazuje naprężenia spoiny dla omawianego przykładu.

Tabela 5.1 Naprężenia spoiny

Literatura [1] Eurokod 3: Projektowanie i wykonanie konstrukcji stalowych - Część 1-8: Projektowanie połączeń; EN 1993-1-8:2005 + AC:2009 [2] Petersen, C.: Konstrukcje stalowe, wydanie 4. Wiesbaden: Springer Vieweg, 2013

Autor

Pani von Bloh zapewnia naszym klientom wsparcie techniczne i jest odpowiedzialna za rozwój programu SHAPE‑THIN oraz konstrukcji stalowych i aluminiowych.

Odnośniki

SHAPE-THIN - Charakterystyki przekrojów cienkościennych

Odniesienia

Europejskie zalecenia dotyczące projektowania prostych połączeń w konstrukcjach stalowych. ECCS - European Convention for Constructional Steelwork, Mem Martins, edition = 1. 2009.

Pobrane

Plik modelu SHAPE-THIN

364 KB

;