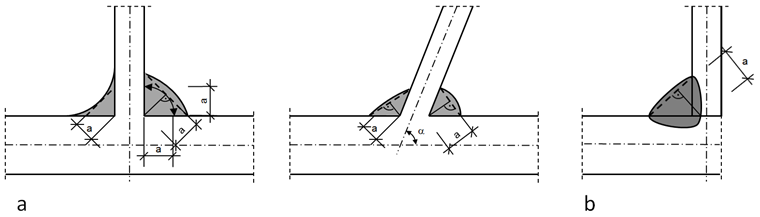
Účinná tloušťka koutového svaru a se má uvažovat jako výška největšího úhelníku (se stejnými nebo nestejnými rameny), vepsaného mezi tavné plochy a povrch svaru, měřeno kolmo k přeponě tohoto trojúhelníku, viz obr. 01.
Únosnost koutových svarů
Návrhová únosnost koutového svaru se má podle 1993-1-8 [1] určit buď metodou uvažující směr namáhání nebo zjednodušenou metodou. Metodu uvažující směr namáhání představíme níže.
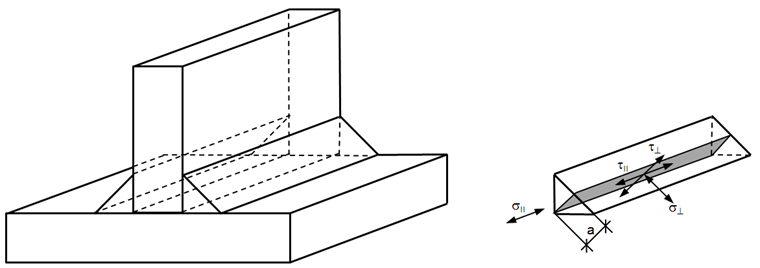
Předpokládá se rovnoměrné rozložení napětí po účinném průřezu svaru, což vede ke vzniku normálového a smykového napětí, jak je znázorněno na obr. 02:
σ⊥ normálové napětí kolmé na osu svaru
Σ|| normálové napětí rovnoběžné s osou svaru
τ⊥ smykové napětí (v účinné rovině průřezu) kolmé na osu svaru
τ|| smykové napětí (v účinné rovině průřezu) rovnoběžné s osou svaru
Při ověřování návrhové únosnosti svaru se neuvažuje normálové napětí rovnoběžné s osou svaru σ||.
Únosnost koutového svaru je dostatečná, jsou-li splněny obě následující podmínky:
kde
fu jmenovitá hodnota meze pevnosti nejslabší spojované části v tahu
βw korelační součinitel (viz EN 1993-1-8, tabulka 4.1)
γM2 dílčí součinitel spolehlivosti pro únosnost svarů
Příklad použití
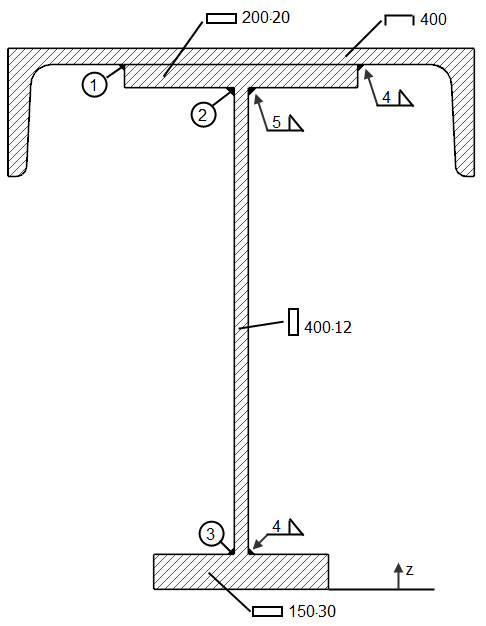
V našem příkladu posoudíme svary nosníku znázorněného na obr. 03, který přebíráme z literatury [2].
Materiál: S235, fu = 36,0 kN/cm², βw = 0,8
Vnitřní síly: Vz = 350 kN
Těžiště
Moment setrvačnosti
Vzhledem k těžišťové ose činí moment setrvačnosti:
Statické momenty
Statické momenty se vzhledem k těžišťové ose stanoví pro části průřezu připojené svary ➀, ➁ a ➂ následově:
Sy,1 = A1 ∙ (zS,1 - zS) = 91,48 ∙ (43,72- 30,88) = 1 175 cm³
Sy, 2 = Sy, 1 + A2 ∙ (zS, 2 - zS ) = 1175 + 40,00 ∙ (44,00 - 30,88) = 1 700 cm³
Sy, 3 = A3 ∙ (zS - zS, 3 ) = 45,00 ∙ (30,88 - 1,50) = 1 322 cm³
Posouzení svarů
SHAPE-THIN
V programu SHAPE-THIN můžeme vypočítat smykové napětí na koutových svarech (v účinné rovině průřezu) rovnoběžné s osou svaru τ|| a ověřit únosnost. Při zadávání modelu je třeba dát pozor na to, aby svar spojoval hrany dvou prvků. Jedním z těchto prvků může být i nulový prvek.
Ve sloupci H „Průběžný prvek“ v tabulce 1.6 Svary lze zadat průběžné prvky. U těchto prvků se nebudou počítat žádná napětí na svarech. Pokud ve sloupci H neuvedeme žádný prvek, pak se napětí na svarech budou zjišťovat u všech prvků, které svar spojuje. Tyto prvky jsou uvedeny ve sloupci B „Prvky č.“.
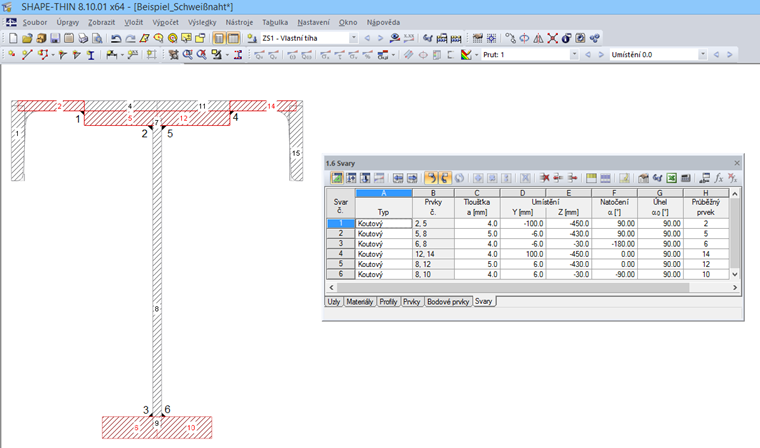
Na Obr. 04 vidíme zadání svarů v našem příkladu.
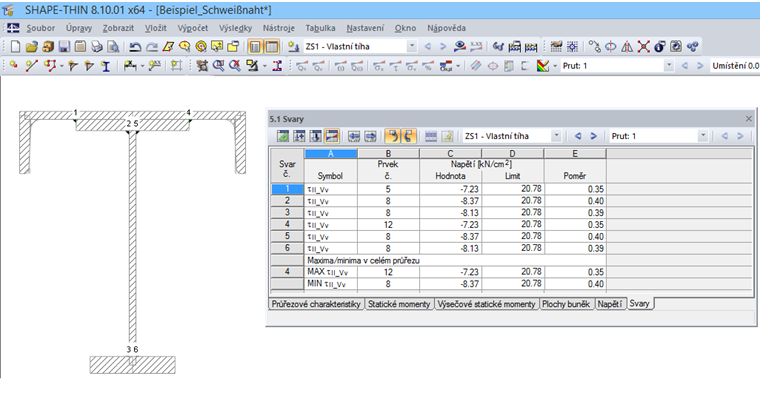
V tabulce 5.1 Svary se zobrazí napětí τ|| na svarech, které jsme zadali v tabulce 1.6 Svary. Na obr. 05 vidíme napětí na svarech v našem příkladu.
Literatura
[1] - Eurokód 3: Navrhování ocelových konstrukcí – Část 1-8: Navrhování styčníků; EN 1993-1-8:2006-12
[2] - Petersen, C.: Stahlbau, 4. vydání. Wiesbaden: Springer Vieweg, 2013