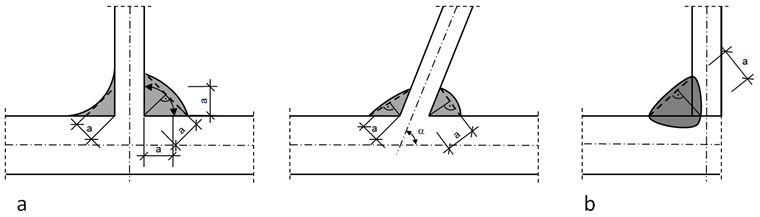
L'épaisseur efficace de soudure a d'une soudure d'angle doit être considérée comme la hauteur du plus grand triangle (avec des branches égales ou inégales) qui peut être inscrit dans les faces de fusion et la surface de soudure, mesurée perpendiculairement au côté extérieur de ce triangle; voir la Figure 01.
Résistance de calcul des soudures d'angle
Selon 1993-1-8 [1] , la résistance de calcul d'une soudure d'angle est généralement déterminée à l'aide de la méthode directionnelle ou de la méthode simplifiée. La méthode directionnelle est décrite ci-dessous.
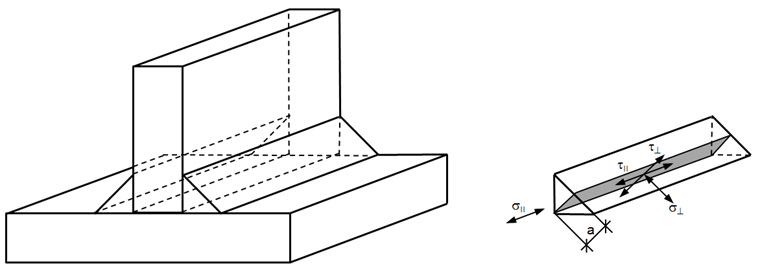
Une distribution uniforme des contraintes est supposée sur la section de la soudure, conduisant aux contraintes normales et aux contraintes de cisaillement indiquées sur la Figure 02, comme suit:
- σ⊥ contrainte normale perpendiculaire à l'axe de soudure
- σ|| contrainte normale parallèle à l'axe de soudure
- τ⊥ contrainte de cisaillement (dans le plan de la surface de la soudure d'angle) perpendiculaire à l'axe de la soudure
- τ|| contrainte de cisaillement (dans le plan de la surface de la soudure d'angle) parallèle à l'axe de la soudure
La contrainte normale σ|| parallèle à l'axe n'est pas considéré lors de la vérification de la résistance de calcul de la soudure d'angle.
La résistance de calcul de la soudure d'angle est suffisante si les conditions suivantes sont remplies:
où
fu est la contrainte de traction ultime nominale de la partie la plus faible connectée,
βw est le facteur de corrélation approprié (voir le Tableau 4.1 de l'EN 1993-1-8)
γM2 est le coefficient partiel de sécurité pour la résistance des soudures.
Exemple
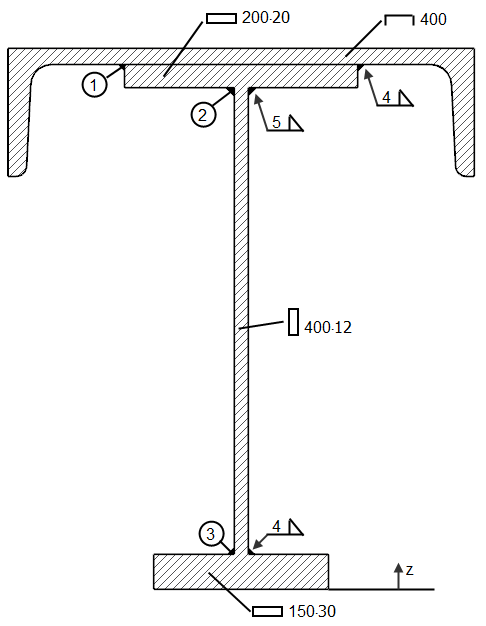
Calcul d'une soudure d'angle de la poutre affichée sur la Figure 03 de [2].
Matériau : S235, fu = 36,0 kN/cm², βw = 0,8
Efforts internes: Vz = 350 kN
Centre de gravité
Moment d'inertie
En ce qui concerne le centre de gravité, le moment d'inertie est:
Moments statiques
En ce qui concerne le centre de gravité, les moments statiques des sections connectées sont calculés à l'aide des soudures , et :
Sy,1 = A1 ∙ (zS,1 - zS) = 91,48 ∙ (43,72- 30,88) = 1175 cm³
Sy,2 = Sy,1 + A2 ∙ (zS,2 - zS)= 1175 + 40,00 ∙ (44,00 - 30,88) = 1700 cm³
Sy,3 = A3 ∙ (zS - zS,3) = 45,00 ∙ (30,88- 1,50) = 1322 cm³
Calcul de la soudure
SHAPE-THIN
Dans SHAPE-THIN, la contrainte de cisaillement (dans le plan de la surface de la soudure d'angle) parallèle à l'axe de la soudure τ|| peut être calculée sur des soudures d'angle et la résistance peut être calculée. Lors de la modélisation, la soudure doit être connectée aux bords de deux éléments. L'un de ces éléments peut également être un élément fictif.
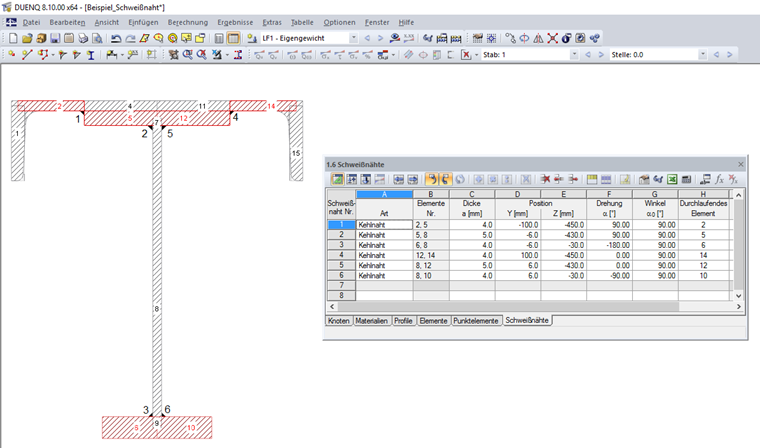
Dans la colonne H «Élément continu» du tableau 1.6 Soudures, vous pouvez définir les éléments continus. Aucune contrainte de soudure n'est calculée sur ces éléments. Si aucun élément n'est spécifié dans la colonne H, les contraintes de soudure sont déterminées sur tous les éléments auxquels la soudure est connectée. Ces éléments peuvent être extraits de la colonne B, « Élément n° ».
La Figure 04 montre la définition de soudure pour l'exemple décrit dans cet article.
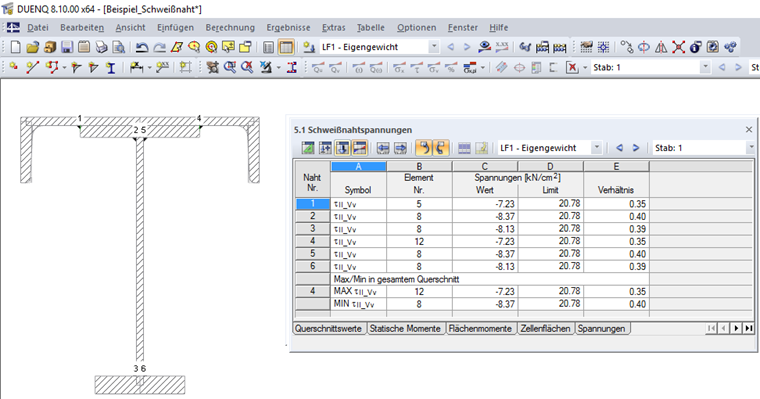
Le tableau 5.1 Soudures affiche les contraintes résultantes τ|| pour les soudures définies dans le Tableau 1.6 Soudures. La Figure 05 montre les contraintes de soudure pour l'exemple décrit dans cet article.
