乔治·温特(George Winter)认为,主杆件在临界屈曲荷载作用下,必须能够完全防止主杆件产生侧向屈曲,并能起到完全支撑的作用,才算是理想的弹簧刚度。 冬天说到 “完全支撑”。 据此,屈曲曲线的过零应位于该弹簧处,因此屈曲曲线本身有两个或更多个波浪,而不是一个。
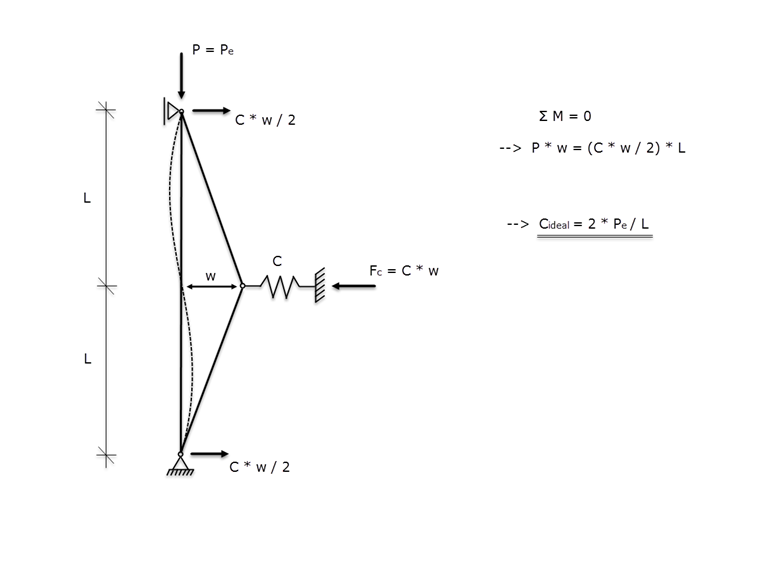
Winter 模型中考虑了一根理想的直线压杆,两边都是端部固定,在中间由一个支撑弹簧约束。 为了确定理想的弹簧刚度,Winter建立了如图01所示的理想模型。
如果跨度相同,那么名义铰基于弯曲屈曲曲线上的拐点进行计算。 临界屈曲荷载 Pe为压缩轴力,杆件在弹簧支座的's范围内位移w尺寸,在消除名义释放周围的区域后,通过下式获得理想弹簧刚度Cideal截面虚部和弯矩平衡的设置条件。
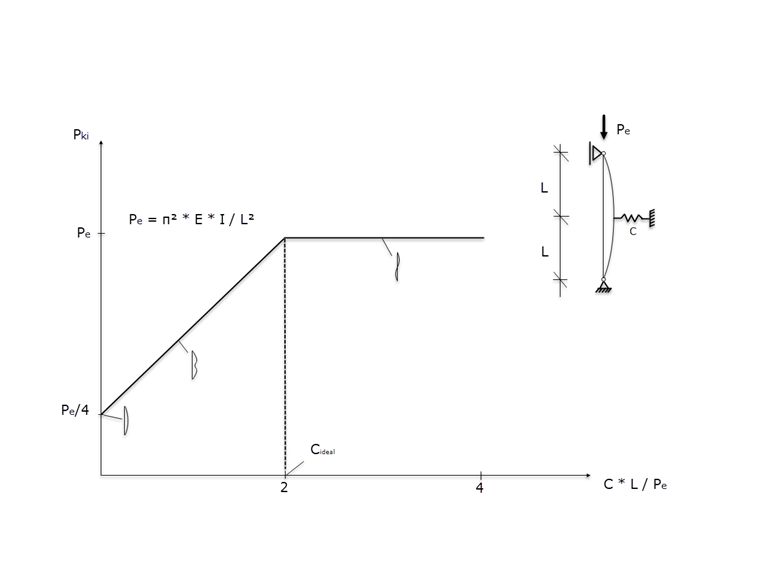
弹簧刚度和临界屈曲荷载之间的关系如图02所示。 因此当弹簧刚度小于 C理想时,在支座弹簧的'区域中会出现一个带有侧向位移的屈曲形状。
临界荷载 Pe可以使用附加模块 RSBUCK 和 RF-STABILITY 来计算,也可以手动计算。
计算示例中描述的理想弹簧刚度
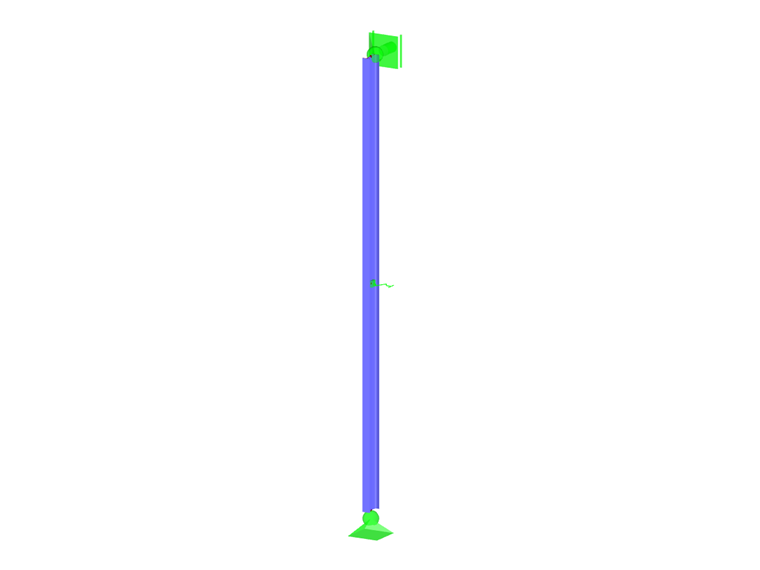
在图03模型中,参数 E = 21000 kN/cm2 、 Iz = 1.318 cm4和 L = 5 m 的受压杆件(IPE 400)在中间通过支撑弹簧约束。
这样得出的临界荷载 Pe为 1.089 kN,由此得出的在杆件中间位置的理想弹簧刚度 Cideal为 436 kN/m。
以一个考虑缺陷的屈曲杆件为例,计算弹性支座的稳定力
除了上述理论考虑外,在对翘曲柱子进行极限荷载试验后,我们确定理论上理想的弹簧刚度对于包含几何缺陷的柱子是不够的。
相应地,图01中的变形w通过预变形w0到wtot进行补充。
w总= w + w0
绕假想铰(图01)建立弯矩平衡后,的结果是:
P ⋅ (w + w0 ) = C ⋅ w ⋅ L/2
计算结果是:
|
wges |
Gesamtverformung aus Knickauslenkung und Vorkrümmung |
|
w0 |
Vorverformung aus Vorkrümmung aufgrund geometrischer Imperfektion |
|
P |
Vorhandene Drucknormalkraft im Knickstab |
|
C |
Federsteifigkeit der seitlichen Stützfeder |
|
L |
Stützweite zwischen Auflager und Stützfeder |
对于 Cideal = 2 ⋅ Pe/L:
|
wges |
Gesamtverformung aus Knickauslenkung und Vorkrümmung |
|
w0 |
Vorverformung aus Vorkrümmung aufgrund geometrischer Imperfektion |
|
P |
Vorhandene Drucknormalkraft im Knickstab |
|
Pe |
Verzweigungslast im Knickstab |
根据公式得出侧重点 Fc为:
稳定扭矩 Fc可以由下列参数确定:
- 实际压力 P = 500 kN
- 支座和支座弹簧之间的跨度 L = 5 m
- 缺陷的初弯曲 w0 = L总的/300 = 10/300 = 0.0333 m
临界荷载 Pe = 1.089 kN
得出稳定荷载 Fc = 12,3 kN。 RFEM 得出的值为 11.7 kN。
概述总结
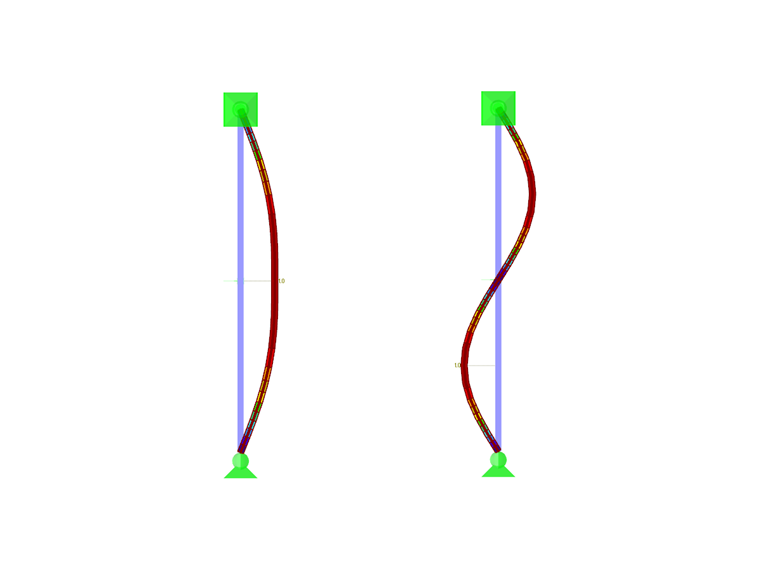
如果要检查弹簧刚度的正确性,可以使用 RF-STABILITY 的结果。 第一个振型是双波屈曲曲线,在弹簧支承下交零,第二种振型是单波屈曲曲线,在弹簧支承下(图 04)。 两者具有近似相同的临界屈曲荷载。