Secondo George Winter, la rigidezza ideale della molla è quella che è almeno necessaria per prevenire completamente l'instabilità laterale dell'asta principale per quanto riguarda il suo carico critico e per agire di conseguenza come un vincolo esterno completo. Winter parla di "controvento completo". In base a ciò, l'attraversamento per lo zero della curva di instabilità dovrebbe essere posizionato su questa molla di vincolo, in modo che la curva di instabilità stessa abbia due o più onde invece di una.
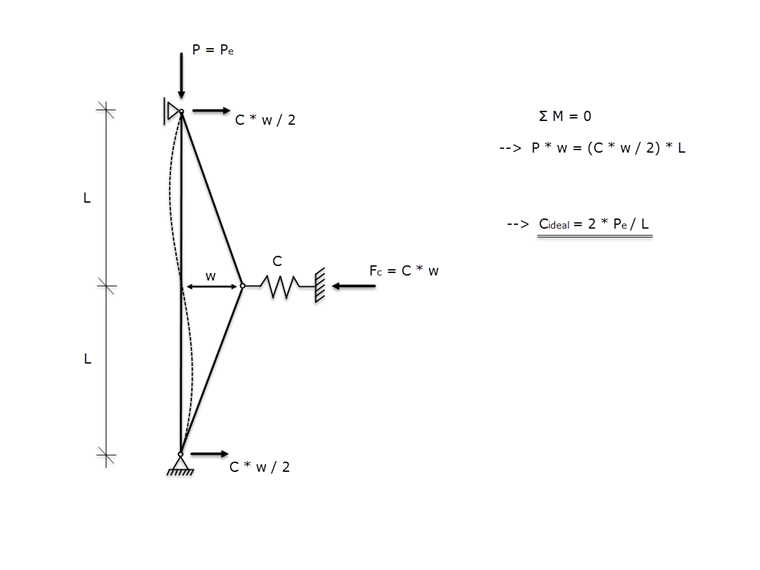
Nel modello Winter, viene considerata un'asta compressa idealmente diritta con estremità incernierate su entrambi i lati, che è vincolata al centro da una molla di supporto. Per determinare la rigidezza ideale della molla, Winter ha sviluppato il modello idealizzato mostrato nell'immagine 01.
Lo svincolo fittizio si basa sull'assunzione di un punto di flesso nella curva di instabilità flessionale, se le lunghezze delle campate sono le stesse. Se il carico critico di instabilità Pe viene applicato come forza assiale di compressione e l'asta è spostata della dimensione w nella regione della molla del vincolo 's, otteniamo la rigidezza ideale della molla Cideale, dopo aver liberato la zona intorno allo svincolo fittizio di tagli immaginari e impostazione delle condizioni per l'equilibrio del momento.
|
Cideal |
Rigidezza ideale della molla |
|
Pe |
Carico critico |
|
L |
Campata tra il vincolo esterno e la molla del vincolo esterno |
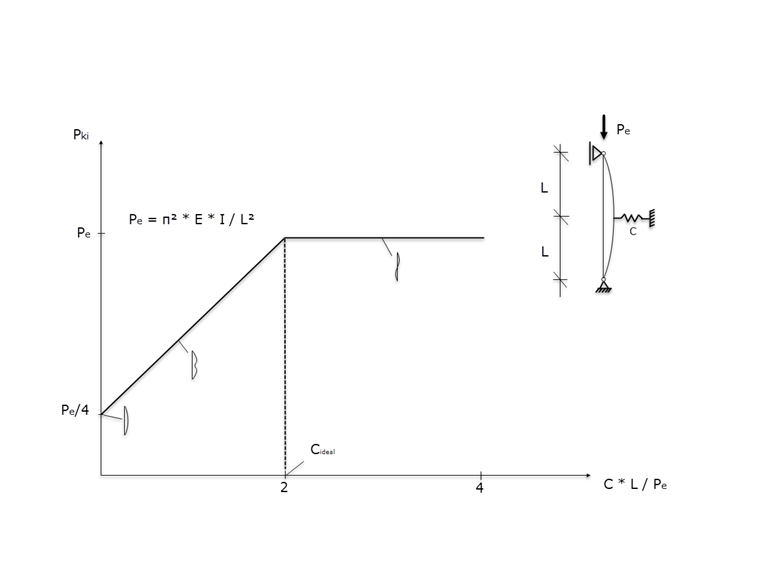
Questa correlazione tra la rigidezza della molla e il carico critico di instabilità risulta nella funzione mostrata nella Figura 02. Pertanto, una forma di instabilità con spostamento laterale nella regione della molla del vincolo 's si verifica per rigidezze della molla inferiori a Cideal.
Il carico critico Pe può essere determinato con i moduli aggiuntivi RSBUCK e RF-STABILITY, o manualmente, come segue.
|
Pe |
Carico critico |
|
E |
Modulo elastico |
|
I |
momento di inerzia |
|
L |
Campata tra il vincolo esterno e la molla del vincolo esterno |
Determinazione della rigidezza ideale della molla descritta dall'esempio
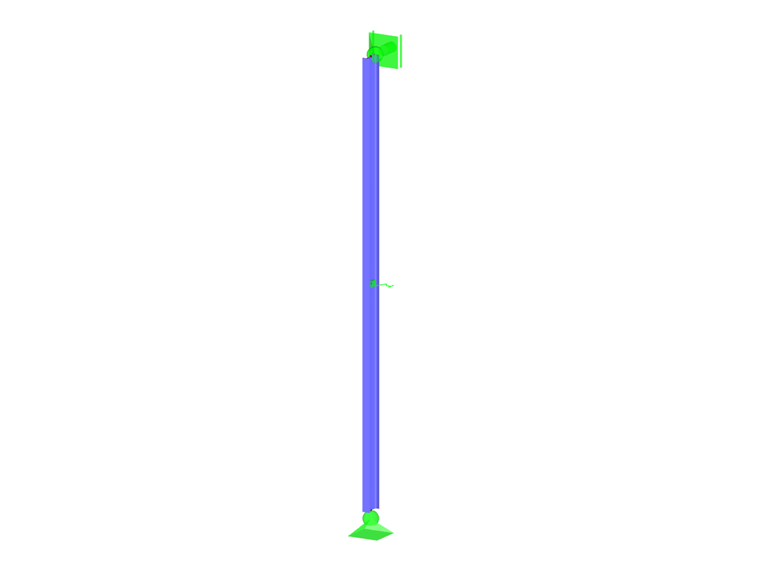
Nel modello (Figura 03), un'asta compressa (IPE 400) con estremità incernierate e i parametri E = 21.000 kN/cm2, Iz = 1.318 cm4 e L = 5 m è trattenuta al centro da una molla di supporto.
Ciò si traduce in un carico critico Pe di 1.089 kN, che si traduce in una rigidezza ideale della molla Cideale per la molla di vincolo definita nel centro dell'asta di 436 kN/m.
Determinazione della forza stabilizzante nella molla di vincolo utilizzando l'esempio di un'asta instabile con un'imperfezione
Dopo aver eseguito le prove di carico ultimo su colonne instabili in aggiunta alle considerazioni teoriche sopra menzionate, abbiamo accertato che la rigidezza elastica teoricamente ideale è insufficiente per le colonne con imperfezioni geometriche.
Di conseguenza, la deformazione w dall'immagine 01 è integrata dalla predeformazione da w0 a wtot.
wtot = w + w0
Dopo aver impostato l'equilibrio del momento attorno alla cerniera teorica (Figura 01), il risultato è:
P ⋅ (w + w0 ) = C ⋅ w ⋅ L/2
Ciò si traduce in:
|
wges |
Gesamtverformung aus Knickauslenkung und Vorkrümmung |
|
w0 |
Vorverformung aus Vorkrümmung aufgrund geometrischer Imperfektion |
|
P |
Vorhandene Drucknormalkraft im Knickstab |
|
C |
Federsteifigkeit der seitlichen Stützfeder |
|
L |
Stützweite zwischen Auflager und Stützfeder |
E per Cideale = 2 ⋅ Pe/L:
|
wges |
Gesamtverformung aus Knickauslenkung und Vorkrümmung |
|
w0 |
Vorverformung aus Vorkrümmung aufgrund geometrischer Imperfektion |
|
P |
Vorhandene Drucknormalkraft im Knickstab |
|
Pe |
Verzweigungslast im Knickstab |
Sulla base di queste equazioni, la forza stabilizzante Fc risulta in:
|
Fc |
Forza di stabilizzazione laterale |
|
C |
Rigidezza della molla del vincolo laterale |
|
w |
Spostamento laterale della barra di instabilità al centro |
|
P |
Forza assiale di compressione nell'asta di instabilità |
|
L |
Luce di campata tra carico di supporto e molla dello stesso |
|
w0 |
Deformazione iniziale da camber per imperfezione geometrica |
|
Pe |
Carico critico dell'asta di instabilità |
La forza stabilizzante Fc può quindi essere determinata dai seguenti parametri:
- Forza di compressione esistente P = 500 kN
- Luce tra il vincolo esterno e la molla del vincolo esterno L = 5 m
- Controfreccia dall'imperfezione w0 = Ltotale/300 = 10/300 = 0,0333 m
Carico critico Pe = 1.089 kN
Ciò si traduce in un carico stabilizzante Fc = 12,3 kN. RFEM determina 11,7 kN.
Conclusione
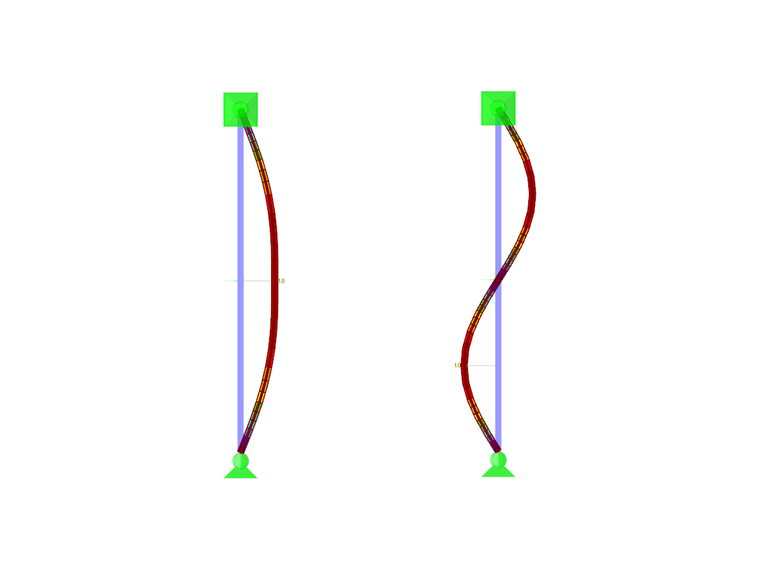
Per verificare la correttezza della rigidezza della molla determinata, è possibile guardare i risultati di RF-STABILITY. La prima forma modale è una curva di instabilità a doppia onda con passaggio per lo zero a livello della molla del vincolo esterno, mentre la seconda forma è una curva di instabilità a onda singola supportata dalla molla del vincolo esterno (Figura 04). Entrambi hanno approssimativamente lo stesso carico critico.