Según George Winter, la rigidez elástica ideal es aquella que es al menos necesaria para evitar completamente el pandeo lateral de la barra principal con respecto a su carga crítica de pandeo y actuar en consecuencia como un apoyo completo. Winter habla de "arriostramiento completo". Según esto, el paso por cero de la curva de pandeo debe ubicarse en este muelle de apoyo, de modo que la curva de pandeo en sí tenga dos o más ondas en lugar de una.
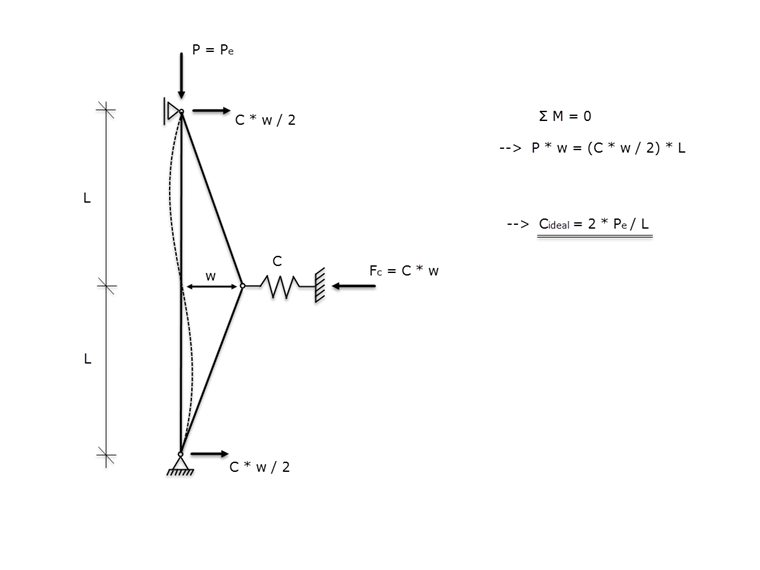
En el modelo de Winter, se considera una barra sometida a compresión idealmente recta con extremos articulados en ambos lados, y que está restringida en su mitad por un muelle de apoyo. Para determinar la rigidez elástica ideal, Winter desarrolló el modelo idealizado que se muestra en la imagen 01.
La liberación teórica se basa en la suposición de un punto de inflexión en la curva de pandeo por flexión, con las longitudes del vano iguales. Si la carga crítica de pandeo Pe se aplica como un esfuerzo axil de compresión y la barra se desplaza por la dimensión w en la región del muelle del apoyo, obtenemos la rigidez elástica Cideal, después de despejar la zona alrededor de la liberación teórica mediante cortes imaginarios y ajustando condiciones al alza para el equilibrio de momentos.
|
Cideal |
Ideale Federsteifigkeit |
|
Pe |
Verzweigungslast |
|
L |
Stützweite zwischen Auflager und Stützfeder |
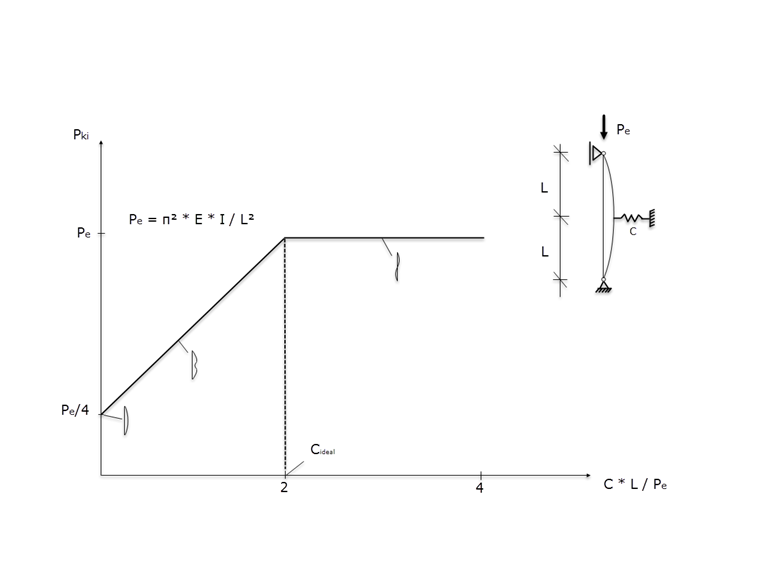
Esta correlación entre la rigidez elástica y la carga crítica de pandeo da como resultado la función que se muestra en la imagen 02. Por lo tanto, se produce una forma de pandeo con desplazamiento lateral en la región del muelle de apoyo para rigideces elásticas menores que Cideal.
La carga crítica Pe se puede determinar con los módulos adicionales RSBUCK y RF-STABILITY, o bien manualmente, como se indica a continuación.
|
Pe |
Verzweigungslast |
|
E |
Elastizitätsmodul |
|
I |
Flächenträgheitsmoment |
|
L |
Stützweite zwischen Auflager und Stützfeder |
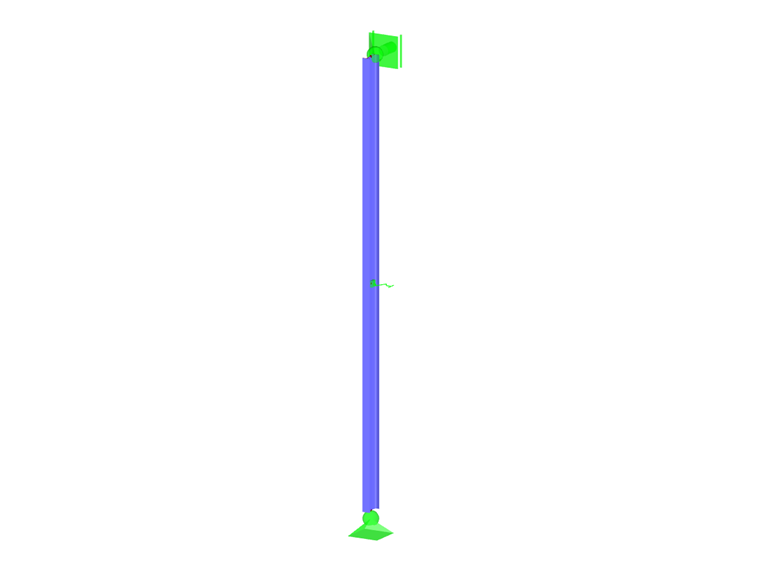
Determinación de la rigidez elástica ideal descrita por un ejemplo
En el modelo (imagen 03), una barra a compresión (IPE 400) con extremos articulados y los parámetros E = 21.000 kN/cm², Iz = 1.318 cm 4 y L = 5 m está coaccionada en el medio por un muelle de apoyo.
Esto da como resultado una carga crítica Pe de 1.089 kN, que da como resultado una rigidez elástica Cideal para el muelle de apoyo definido en el centro de la barra de 436 kN/m.
Determinación de la fuerza de estabilización en el muelle de apoyo utilizando el ejemplo de una barra a pandeo con una imperfección
Después de realizar pruebas de carga última en pilares con pandeo, además de las consideraciones teóricas mencionadas anteriormente, determinamos que la rigidez elástica teóricamente ideal es insuficiente para pilares con imperfecciones geométricas.
En consecuencia, la deformación w de la imagen 01 se complementa con la predeformación de w0 a wtot.
wtot = w + w0
Después de establecer el equilibrio de momentos sobre la articulación teórica (imagen 01), el resultado es:
P ⋅ (w + w0 ) = C ⋅ w ⋅ L / 2
Esto da como resultado:
|
wges |
Gesamtverformung aus Knickauslenkung und Vorkrümmung |
|
w0 |
Vorverformung aus Vorkrümmung aufgrund geometrischer Imperfektion |
|
P |
Vorhandene Drucknormalkraft im Knickstab |
|
C |
Federsteifigkeit der seitlichen Stützfeder |
|
L |
Stützweite zwischen Auflager und Stützfeder |
Y para Cideal = 2 ⋅ Pe / L:
|
wges |
Gesamtverformung aus Knickauslenkung und Vorkrümmung |
|
w0 |
Vorverformung aus Vorkrümmung aufgrund geometrischer Imperfektion |
|
P |
Vorhandene Drucknormalkraft im Knickstab |
|
Pe |
Verzweigungslast im Knickstab |
Basándose en estas ecuaciones, la fuerza estabilizadora Fc da como resultado:
|
Fc |
Seitliche Stabilisierungskraft |
|
C |
Federsteifigkeit der seitlichen Stützung |
|
w |
Seitliche Auslenkung des Knickstabes in der Mitte |
|
P |
Drucknormalkraft im Knickstab |
|
L |
Stützweite zwischen Auflager und Stützfeder |
|
w0 |
Vorverformung aus Vorkrümmung aufgrund geometrischer Imperfektion |
|
Pe |
Verzweigungslast des Knickstabes |
Por lo tanto, la fuerza de estabilización Fc se puede determinar a partir de los siguientes parámetros:
- Fuerza de compresión existente P = 500 kN
- Vano entre apoyo y muelle de apoyo L = 5,00 m
- Imperfección de curvatura w0 = Ltotal / 300 = 10 / 300 = 0,0333 m
Carga crítica Pe = 1.089 kN
Esto da como resultado una carga estabilizadoraFc = 12,3 kN. RFEM determina 11,7 kN.
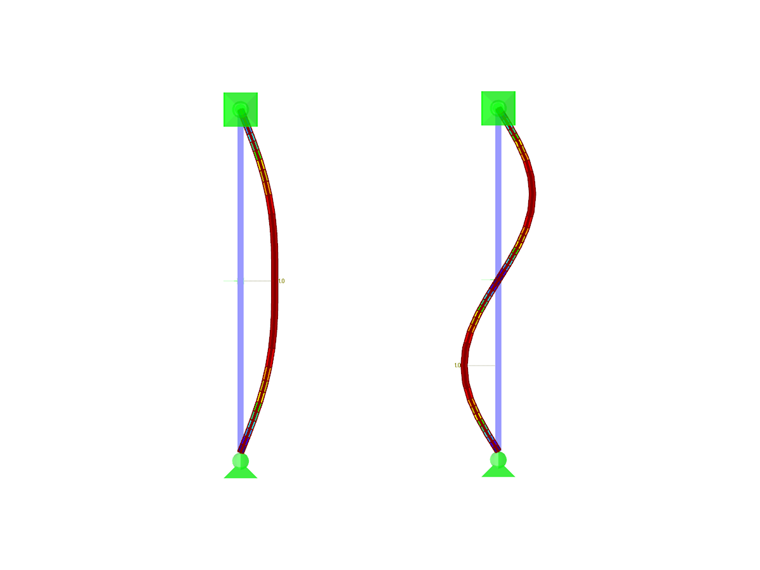
Conclusión
Para comprobar la exactitud de la rigidez elástica determinada, puede consultar los resultados de RF-STABILITY. La primera deformada del modo es una curva de pandeo de onda doble con paso por cero en el nivel del muelle del apoyo, mientras que la segunda deformada es una curva de pandeo de una onda apoyada por el muelle del apoyo (imagen 04). Ambos tienen aproximadamente la misma carga crítica de pandeo.
Base de datos de conocimientos
.png?mw=350&hash=6eaa339e57e511d092af43ce013e521254c93d0f)
_1.jpg?mw=350&hash=ab2086621f4e50c8c8fb8f3c211a22bc246e0552)
-querkraft-hertha-hurnaus.jpg?mw=350&hash=3306957537863c7a7dc17160e2ced5806b35a7fb)
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
