Ideální tuhost pružiny je podle George Wintera taková tuhost, která je zapotřebí přinejmenším k tomu, aby s ohledem na kritické zatížení hlavního prutu zcela zamezila jeho příčnému vybočení, a působila tak jako plnohodnotná podpora. Winter hovoří o „úplném ztužení“. V místě této pružné podpory má proto vzpěrnostní křivka procházet nulovým bodem, a křivka vzpěrné pevnosti má tak sama dvě nebo více vln místo jedné.
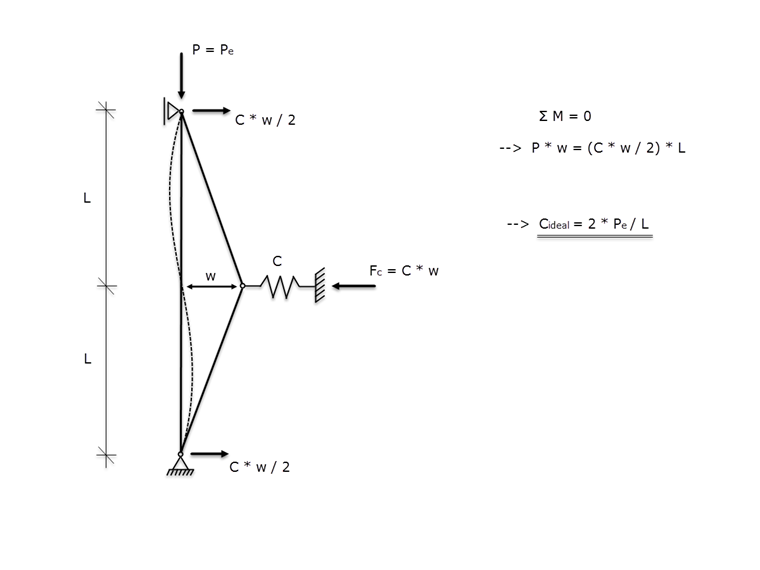
Winterův model vychází z ideálního přímého tlačeného prutu s kloubem na obou stranách, který je ve svém středu zajištěn pružnou podporou. Pro stanovení ideální tuhosti pružiny vytvořil Winter idealizovaný model, který je znázorněn na obr. 01.
Fiktivní kloub je založen na předpokladu inflexního bodu na křivce vzpěrné pevnosti se stejnými vzdálenostmi mezi podporami. Pokud jako tlakovou osovou sílu uvažujeme kritickou sílu Pe a prut se v oblasti pružné podpory posouvá o w, dostaneme po řezu na fiktivním kloubu a po ustavení momentové rovnováhy ideální tuhost pružiny Cideal.
| Cideal | ideální tuhost pružiny |
| Pe | kritické zatížení |
| L | vzdálenost mezi uložením a pružnou podporou |
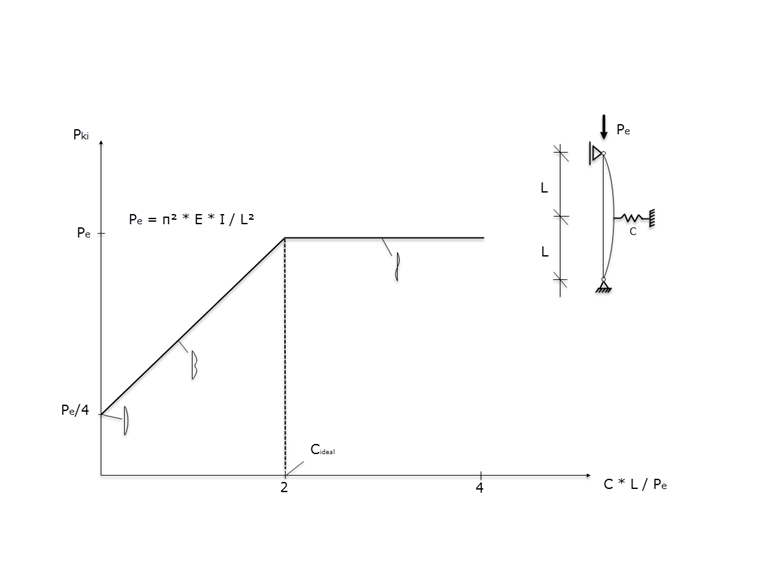
Ze vztahu mezi tuhostí pružiny a kritickou silou lze stanovit funkci znázorněnou na obr. 02. U tuhostí pružiny menších než Cideal tak lze pozorovat tvar vybočení s příčným posunem v oblasti pružné podpory.
Kritické zatížení Pe lze stanovit pomocí přídavných modulů RSBUCK a RF-STABILITY nebo ručním výpočtem následovně.
| Pe | kritické zatížení |
| E | modul pružnosti |
| I | moment setrvačnosti plochy |
| L | vzdálenost mezi uložením a pružnou podporou |
Stanovení ideální tuhosti pružiny na konkrétním příkladu
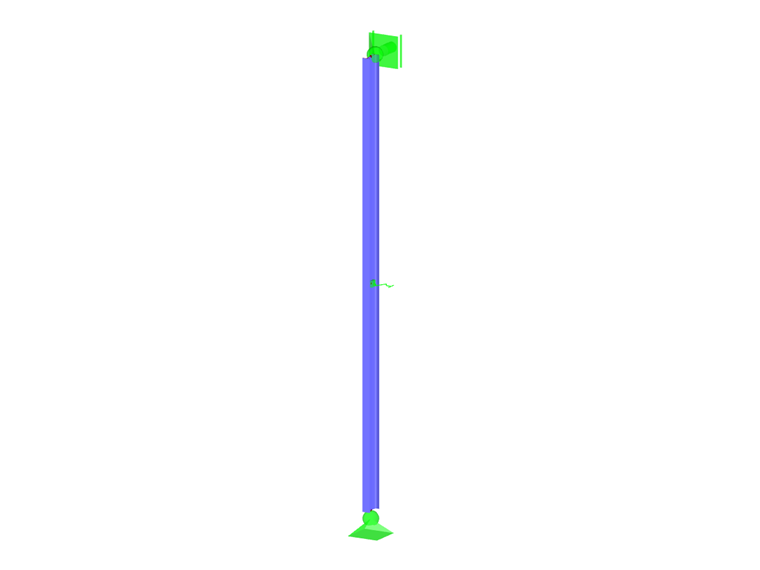
V modelu (obr. 03) je tlačený prut (IPE 400) s klouby na obou stranách a parametry E = 21 000 kN/cm², Iz = 1 318 cm4 a L = 5 m zajištěn ve svém středu pružnou podporou.
Kritické zatížení Pe činí 1 089 kN, z čehož plyne ideální tuhost pružiny Cideal 436 kN/m pro pružnou podporu zadanou uprostřed prutu.
Stanovení stabilizační síly v pružné podpoře na příkladu vzpěrného prutu s imperfekcí
Po provedení zkoušek mezního zatížení na vzpěrných sloupech pro doplnění výše uvedené teorie bylo zjištěno, že teoreticky ideální tuhost pružiny u sloupů s geometrickými imperfekcemi nestačí.
Deformaci w z obr. 01 proto rozšíříme o počáteční deformaci w0 na wtot.
wtot = w + w0
Po ustavení momentové rovnováhy okolo fiktivního kloubu (obr. 01) platí:
P ⋅ (w + w0) = C ⋅ w ⋅ L / 2
Z toho vyplývá:
| wtot | celková deformace od vybočení a počátečního prohnutí |
| w0 | počáteční prohnutí jako deformace vlivem geometrické imperfekce |
| P | návrhová tlaková osová síla ve vzpěrném prutu |
| C | tuhost pružiny příčné podpory |
| L | vzdálenost mezi uložením a pružnou podporou |
A pro Cideal = 2 ⋅ Pe / L:
| wtot | celková deformace od vybočení a počátečního prohnutí |
| w0 | počáteční prohnutí jako deformace vlivem geometrické imperfekce |
| P | návrhová tlaková osová síla ve vzpěrném prutu |
| Pe | kritická síla ve vzpěrném prutu |
Stabilizační síla Fc se určí z těchto vztahů:
| Fc | příčná stabilizační síla |
| C | tuhost pružiny příčné podpory |
| w | příčný průhyb vzpěrného prutu uprostřed |
| P | tlaková osová síla ve vzpěrném prutu |
| L | vzdálenost mezi uložením a pružnou podporou |
| w0 | počáteční prohnutí jako deformace vlivem geometrické imperfekce |
| Pe | kritická síla ve vzpěrném prutu |
Stabilizační sílu Fc tak lze stanovit na základě následujících parametrů:
- Návrhová tlaková síla P = 500 kN
- Vzdálenost mezi uložením a pružnou podporou L = 5,00 m
- Imperfekce ve tvaru počátečního prohnutí w0 = Ltotal / 300 = 10 / 300 = 0,0333 m
Kritické zatížení Pe = 1 089 kN
Výsledkem je stabilizační zatížení Fc = 12,3 kN. RFEM stanoví 11,7 kN.
Závěr a výhled
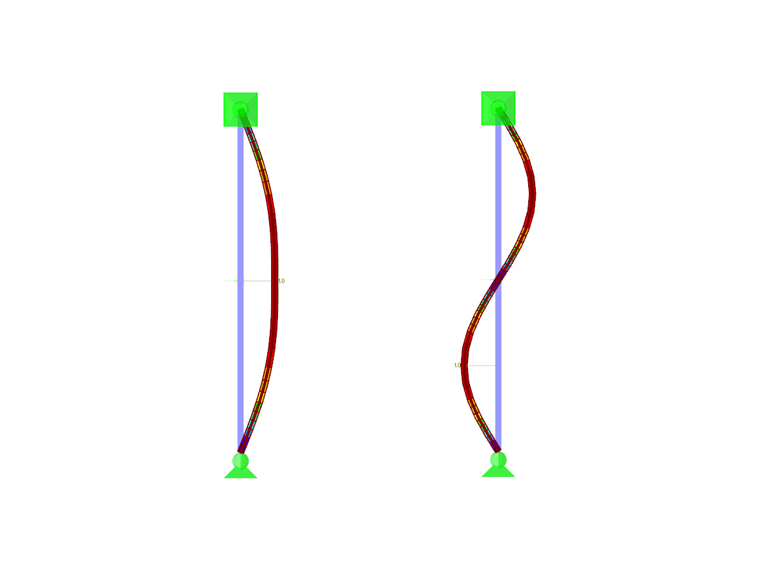
Pro kontrolu správnosti stanovené tuhosti pružiny se lze podívat na výsledky z modulu RF-STABILITY. První vlastní tvar odpovídá dvouvlnové vzpěrnostní křivce procházející nulovým bodem v úrovni pružné podpory, zatímco druhý vlastní tvar představuje jednovlnová vzpěrnostní křivka s podepřením v pružné podpoře (obr. 04). Oba vykazují přibližně stejné kritické zatížení.
