4459x

001502

Dipl.-Ing. (FH) Bastian Kuhn, M.Sc.

16.01.2018

Effort par boulon de l’assemblage principal de poutre

RF-/JOINTS Timber to Timber permet de concevoir des assemblages de poutres principale et secondaire. Cet article explique la détermination d’effort dans le boulon d’une poutre connectée à une poutre principale rigide en torsion.

Système

La détermination des efforts dans le boulon rend la vérification possible uniquement dans le plan principal de la paire de boulons. Les forces dans l’autre plan du boulon ne sont pas considérées par le module. Ainsi, si des efforts internes V_y et V_z existent, seul le plan sélectionné (en général V_z) est considéré. Toutefois, vous pouvez sélectionner le plan de l’assemblage dans le module (Figure 02).

Plan de l’assemblage

Dans notre exemple, la torsion bi-axiale est définie pour mettre en lumière cette méthode de vérification. Dans un système 3D, des forces dans la direction y et z agiront inévitablement. Si ces forces deviennent trop importantes, une interaction avec

\begin{array}{l} f_{ax, k} = 0.52 \cdot \emptyset^{- 0.5} \cdot l_{ef}^{- 0.1} \cdot ρ_{k}^{0.8} = 0.52 \cdot 8 {mm}^{- 0.5} \cdot 90 {mm}^{- 0.1} \cdot 350^{0.8} = 11.27 N / {mm}^{2} \\ F_{ax, Rk} = \frac{n_{ef} \cdot f_{ax, k} \cdot d \cdot l_{ef} \cdot k_{d}}{1.2 \cos^{2} α \sin^{2} α} = \frac{11.27 \cdot 8 mm \cdot 90 mm \cdot 1}{1.2 \cos^{2} 30 \sin^{2} 30} = 7.96 kN \\ f_{tens, k} = 20 kN \\ f_{c, k} = 50 kN \end{array}

Formule 1

peut être déterminée comme estimation conservatrice.

Système

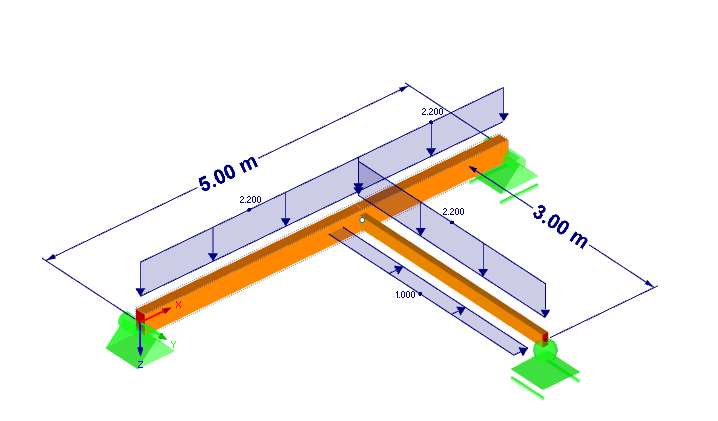
Poutre principale = 14/26 GL24c
Poutre connectée = 10/16 C24
Travée de la poutre principale = 5 m
Travée de la poutre connectée = 3 m
Charge z = 2,2 kN/m (self‑weight par défaut)
Charge y = 1,0 kN/m
Effort tranchant de connexion Vz = 3,38 kN
Effort tranchant de connexion Vy = 1,13 kN
Angle de vissage des boulons les uns par rapport aux autres = 45 °
Classe de durée de charge permanente

Vérification des boulons

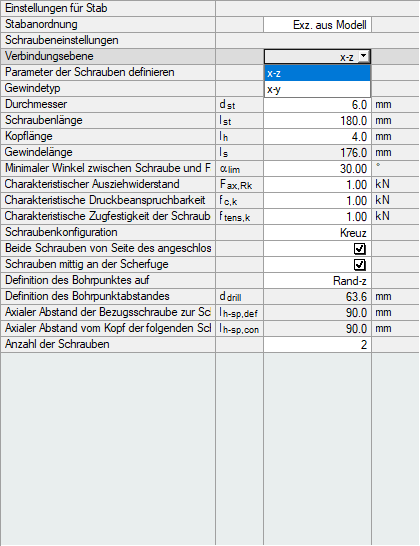
Le type d’assemblage 2 est sélectionné dans le module pour l’assemblage de la poutre principale avec la poutre connectée. Les nœuds sont ensuite sélectionnés, puis les charges sont définies. Des informations de base au sujet de l’entrée peuvent être trouvées dans le manuel pour le module. Dans la fenêtre « Géométrie », le plan x-z est sélectionné pour l’assemblage pour la définition de la première vérification.

Type d’assemblage 2

La capacité portante de charge du boulon est définie manuellement selon [1].

\begin{array}{l} F_{def} = \cos (α N_{def}) \cdot N \cos (α V_{def}) \cdot V = 0 \cos 45 ° \cdot 3.38 = 2.39 kN \\ F_{con} = \cos (α N_{con}) \cdot N \cos (α V_{con}) \cdot V = 0 \cos 45 ° \cdot 3.38 = 2.39 kN \end{array}

Formule 2

Pour en savoir plus sur la géométrie, nous vous invitons à consulter le manuel du module (disponible en anglais).

Vérification

La vérification des efforts dans les boulons est affichée ci-dessous. Dans le logiciel, cette vérification est réalisée sous les numéros de vérification interne 4103 et 4104.

Effort du boulon dans le plan x-z :

F_{ax, Rd} = \frac{0.6 \cdot 7.96}{1.3} = 3.67 kN \to \frac{2.39}{3.67} = 0.65

Formule 3

Forces par boulon dans le plan x-z

Vérification :

\begin{array}{l} F_{def} = \cos (α N_{def}) \cdot N \cos (α V_{def}) \cdot V = 0 \cos 45 ° \cdot 1.13 = 0.80 kN \\ F_{con} = \cos (α N_{con}) \cdot N \cos (α V_{con}) \cdot V = 0 \cos 45 ° \cdot 1.13 = 0.80 kN \end{array}

Formule 4

Utilisation = 65%.

Effort par boulon dans le plan x-y :
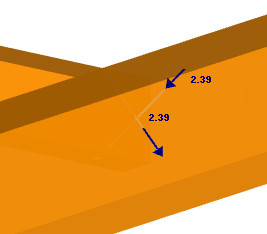
Ci-dessous, la paire de boulon est située et conçue dans un plan pivoté d’environ 90° à cause de la double-flexion.

F_{ax, Rd} = \frac{0.6 \cdot 5.5}{1.3} = 2.53 kN \to \frac{0.8}{2.53} = 0.31

Formule 5

Vérification dans le plan x-y :
Le diamètre est modifié à 6 mm et la longueur de vis à 140 mm. Ainsi en résultent des capacités portantes légèrement différentes. La détermination de la capacité portante n’est pas décrite à nouveau dans cet article.

η_{ges} = \sqrt{0 . 65^{2} 0 . 31^{2}} = 0.72

Formule 6

Utilisation = 31%.

Interaction :

η_{ges} = \sqrt{0, 65^{2} 0, 31^{2}} = 0, 72

Formule 7

Résumé

La superposition manuelle permet de considerer la double flexion dans deux cas avec RF-/JOINTS Timber – Timber to Timber. La résistance en traction et la résistance à l’arrachement sont seulement considérées dans chaque plan respectif.

Littérature

[1]	Eurocode 5 : Conception et calcul des structures en bois - Partie 1-1 : Généralités - Règles communes et règles pour les bâtiments ; DIN EN 1995-1-1:2010-12

Auteur

M. Kuhn est responsable du développement de produits pour les structures en bois et fournit une assistance technique à nos clients.

Téléchargements

Fichier du modèle RFEM

636 KB

;