3955x

001502

Dipl.-Ing. (FH) Bastian Kuhn, M.Sc.

2018-01-16

Siły w śrubach w połączeniu z belką główną

Moduł RF-/JOINTS Timber - Timber to Timber umożliwia obliczanie połączeń między belką główną i drugorzędną. Artykuł wyjaśnia sposób definiowania sił w śrubach belki, połączonej z główną belką, zablokowaną na skręcanie.

Układ

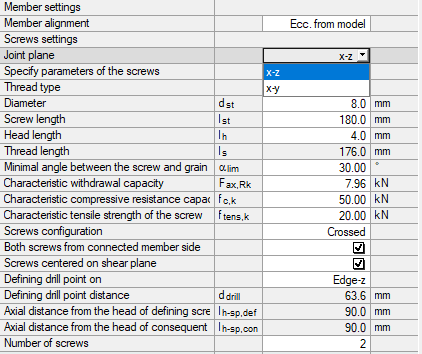
Ze względu na definicję sił w śrubach, obliczenia mogą zostać przeprowadzone w głównej płaszczyźnie pary śrub. Siły w innej płaszczyźnie śruby nie są w module uwzględniane. Falls also Schnittgrößen V_y und V_z vorhanden sind, wird immer nur die gewählte Ebene (im Regelfall V_z) berücksichtigt. Jednakże w module można wybrać płaszczyznę połączenia (Rysunek 02).

Płaszczyzna połączenia

W naszym przykładzie, definiowane jest zginanie dwuosiowe, aby zademonstrować sposób obliczeń. W układzie przestrzennym, w sposób nieunikniony pojawią się siły w kierunku y i z. Falls diese Kräfte zu groß werden, kann als konservative Abschätzung eine Interaktion mit

\begin{array}{l} f_{ax, k} = 0.52 \cdot \emptyset^{- 0.5} \cdot l_{ef}^{- 0.1} \cdot ρ_{k}^{0.8} = 0.52 \cdot 8 {mm}^{- 0.5} \cdot 90 {mm}^{- 0.1} \cdot 350^{0.8} = 11.27 N / {mm}^{2} \\ F_{ax, Rk} = \frac{n_{ef} \cdot f_{ax, k} \cdot d \cdot l_{ef} \cdot k_{d}}{1.2 \cos^{2} α \sin^{2} α} = \frac{11.27 \cdot 8 mm \cdot 90 mm \cdot 1}{1.2 \cos^{2} 30 \sin^{2} 30} = 7.96 kN \\ f_{tens, k} = 20 kN \\ f_{c, k} = 50 kN \end{array}

Wzór 1

durchgeführt werden.

System

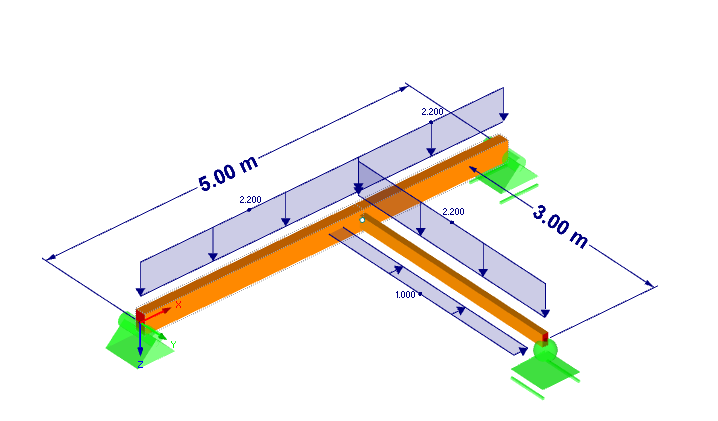
Belka główna = 14/26 GL24c
Belka drugorzędna = 10/16 C24
Rozpiętość belki głównej = 5 m
Rozpiętość belki drugorzędnej = 3 m
Obciążenie z = 2.2 kN/m (ciężar własny ustawiony domyślnie)
Obciążenie y = 1.0 kN/m
Siła tnąca V z = 3.38 kN
Siła tnąca V y = 1.13 kN
Kąt wkrętu śrub = 45 °
Stała KTO

Obliczenia w śrubach

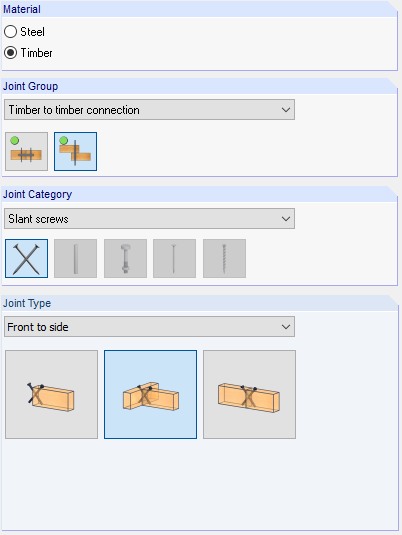
W module dodatkowym wybierany jest typ połączenia 2 dla połączenia między belką główną i drugorzędną. Następnie wybierane są węzły połączenia i definiowane są obciążenia. Ogólne informacje na temat danych wejściowych znajdują się w instrukcji obsługi modułu. W oknie Geometria, w celu zdefiniowania pierwszego obliczenia, wybierana jest płaszczyzna połączenia x-z.

Typ połączenia 2

Die Tragfähigkeit der Schraube wird manuell definiert gemäß [1].

\begin{array}{l} F_{def} = \cos (α N_{def}) \cdot N \cos (α V_{def}) \cdot V = 0 \cos 45 ° \cdot 3.38 = 2.39 kN \\ F_{con} = \cos (α N_{con}) \cdot N \cos (α V_{con}) \cdot V = 0 \cos 45 ° \cdot 3.38 = 2.39 kN \end{array}

Wzór 2

Für weitere Angaben hinsichtlich der Geometrie wird wiederum auf das Handbuch verwiesen.

Warunek projektowy

Poniżej pokazano obliczenia sił w śrubach. W programie oznaczono je wewnętrznymi numerami obliczeń 4103 i 4104.

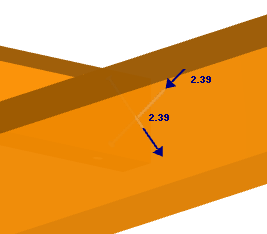
Siły w śrubach w płaszczyźnie x‑z:

F_{ax, Rd} = \frac{0.6 \cdot 7.96}{1.3} = 3.67 kN \to \frac{2.39}{3.67} = 0.65

Wzór 3

Kräfte je Schraube in x-z-Ebene

Weryfikacja:

\begin{array}{l} F_{def} = \cos (α N_{def}) \cdot N \cos (α V_{def}) \cdot V = 0 \cos 45 ° \cdot 1.13 = 0.80 kN \\ F_{con} = \cos (α N_{con}) \cdot N \cos (α V_{con}) \cdot V = 0 \cos 45 ° \cdot 1.13 = 0.80 kN \end{array}

Wzór 4

Wykorzystanie = 65%.

Siły w śrubie w płaszczyźnie x-y:
Poniżej para śrub została umieszczona i obliczona w płaszczyźnie obróconej o 90° ze względu na podwójne zginanie.

F_{ax, Rd} = \frac{0.6 \cdot 5.5}{1.3} = 2.53 kN \to \frac{0.8}{2.53} = 0.31

Wzór 5

Obliczenia w płaszczyźnie x-y:
Średnica została zmieniona na 6 mm, a długość śruby na 140 mm. Tym samym, pojawia się nieco inna nośność. Definiowanie nośności nie jest tu ponownie omawiane.

η_{ges} = \sqrt{0 . 65^{2} 0 . 31^{2}} = 0.72

Wzór 6

Wykorzystanie = 31%.

Interakcja:

\sqrt{V_{z} ² V_{y} ²}

Wzór 7

Podsumowanie

Ręczne superpozycjonowanie umożliwia uwzględnienie podwójnego zginania w dwóch przypadkach w module RF /JOINTS Timber - Timber to Timber. Wytrzymałość na rozciąganie oraz nośność na wyciąganie są uwzględniane tylko w odpowiedniej płaszczyźnie.

Literatura

[1]	Eurocode 5: Bemessung und Konstruktion von Holzbauten - Teil 1-1: Allgemeines - Allgemeine Regeln und Regeln für den Hochbau; DIN EN 1995-1-1:2010-12

Autor

Pan Kuhn jest odpowiedzialny za rozwój produktów do konstrukcji drewnianych i zapewnia wsparcie techniczne dla naszych klientów.

Pobrane

Plik modelu w RFEM

636 KB

;