3955x

001502

Dipl.-Ing. (FH) Bastian Kuhn, M.Sc.

16.1.2018

Síly ve vrutech mezi hlavním a připojeným nosníkem

Modul RF-/JOINTS Timber - Timber to Timber umožňuje posoudit připojení vedlejších nosníků na hlavní nosníky. Výpočet sil ve vrutech si vysvětlíme na příkladu nosníku připojeného na torzně tuhý hlavní nosník.

Systém

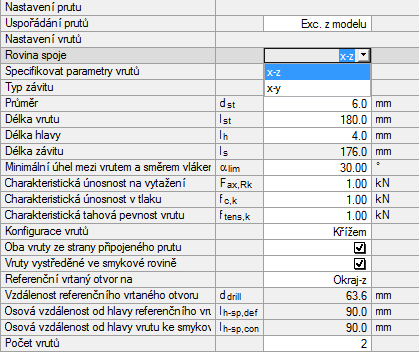
Vzhledem k výpočtu sil ve vrutech je posouzení možné vždy pouze v hlavní rovině dané dvojice vrutů. Síly v jiné rovině vrutu modul nezohledňuje. Falls also Schnittgrößen V_y und V_z vorhanden sind, wird immer nur die gewählte Ebene (im Regelfall V_z) berücksichtigt. Rovinu spoje můžeme ovšem v modulu vybrat (obr. 02).

Rovina spoje

V našem příkladu zadáme dvouosý ohyb, abychom předvedli příslušný způsob posouzení. V prostorové konstrukci tak budou nutně působit síly ve směru y a z. Falls diese Kräfte zu groß werden, kann als konservative Abschätzung eine Interaktion mit

\sqrt{V_{z} ² V_{y} ²}

Vzorec 1

durchgeführt werden.

Systém

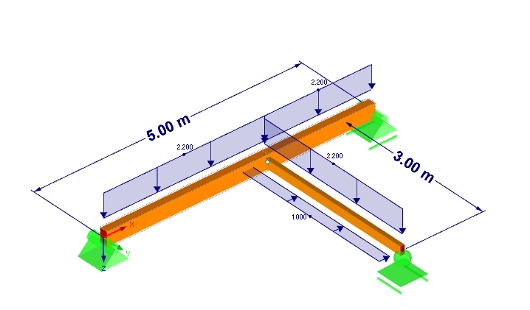
Hlavní nosník = 14/26 GL24c
Připojený nosník = 10/16 C24
Rozpětí hlavního nosníku = 5 m
Rozpětí připojeného nosníku = 3 m
Zatížení z = 2,2 kN/m (vlastní tíha stanovená v programu)
Zatížení y = 1,0 kN/m
Posouvající síla v připojeném prutu Vz = 3,38 kN
Posouvající síla v připojeném prutu Vy = 1,13 kN
Úhel zašroubování vrutů vůči sobě navzájem = 45°
TTZ stálé

Posouzení vrutů

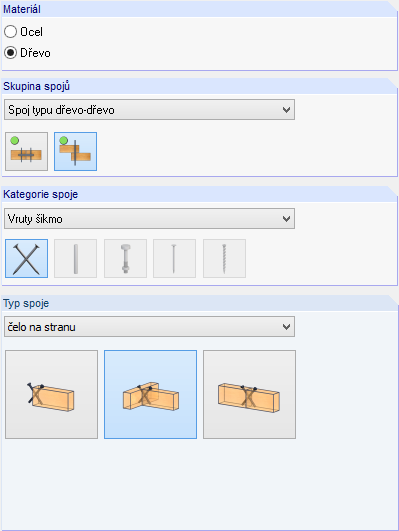
Pro připojení vedlejšího nosníku na hlavní nosník zvolíme v modulu typ spoje 2. Dále vybereme uzel, v němž je vedlejší nosník připojen, a zadáme zatížení. Obecné informace o zadání údajů najdeme v příručce k modulu. V dialogu Geometrie nastavíme pro zadání prvního posouzení rovinu x-z.

Typ spoje 2

Die Tragfähigkeit der Schraube wird manuell definiert gemäß [1].

\begin{array}{l} f_{ax, k} = 0, 52 \cdot \emptyset^{- 0, 5} \cdot l_{ef}^{- 0, 1} \cdot ρ_{k}^{0, 8} = 0, 52 \cdot 8 {mm}^{- 0, 5} \cdot 90 {mm}^{- 0, 1} \cdot 350^{0, 8} = 11, 27 N / {mm}^{2} \\ F_{ax, Rk} = \frac{n_{ef} \cdot f_{ax, k} \cdot d \cdot l_{ef} \cdot k_{d}}{1, 2 \cos^{2} α \sin^{2} α} = \frac{11, 27 \cdot 8 mm \cdot 90 mm \cdot 1}{1, 2 \cos^{2} 30 \sin^{2} 30} = 7, 96 kN \\ f_{tens, k} = 20 kN \\ f_{c, k} = 50 kN \end{array}

Vzorec 2

Für weitere Angaben hinsichtlich der Geometrie wird wiederum auf das Handbuch verwiesen.

Posudek

Následně si ukážeme posouzení sil ve vrutech. V programu se posouzení provádí pod interními čísly 4103 a 4104.

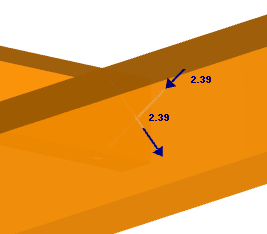
Síla na vrut v rovině x-z:

\begin{array}{l} F_{def} = \cos (α N_{def}) \cdot N \cos (α V_{def}) \cdot V = 0 \cos 45 ° \cdot 3, 38 = 2, 39 kN \\ F_{con} = \cos (α N_{con}) \cdot N \cos (α V_{con}) \cdot V = 0 \cos 45 ° \cdot 3, 38 = 2, 39 kN \end{array}

Vzorec 3

Kräfte je Schraube in x-z-Ebene

Posouzení:

F_{ax, Rd} = \frac{0, 6 \cdot 7, 96}{1, 3} = 3, 67 kN \to \frac{2, 39}{3, 67} = 0, 65

Vzorec 4

Využití = 65 %.

Síla na vrut v rovině x-y:
Vzhledem k dvouosému ohybu nyní vložíme dvojici vrutů do roviny pootočené o 90° a posoudíme ji.

\begin{array}{l} F_{def} = \cos (α N_{def}) \cdot N \cos (α V_{def}) \cdot V = 0 \cos 45 ° \cdot 1, 13 = 0, 80 kN \\ F_{con} = \cos (α N_{con}) \cdot N \cos (α V_{con}) \cdot V = 0 \cos 45 ° \cdot 1, 13 = 0, 80 kN \end{array}

Vzorec 5

Posouzení v rovině x-y:
Průměr upravíme na 6 mm a délku vrutu na 140 mm. Únosnost je proto nepatrně odlišná. Výpočet únosnosti již znovu neuvádíme.

F_{ax, Rd} = \frac{0, 6 \cdot 5, 5}{1, 3} = 2, 53 kN \to \frac{0, 8}{2, 53} = 0, 31

Vzorec 6

Využití = 31 %.

Interakce:

η_{ges} = \sqrt{0, 65^{2} 0, 31^{2}} = 0, 72

Vzorec 7

Závěr

Ruční superpozice nám umožňuje ve dvou případech v modulu RF-/JOINTS Timber – Timber to Timber zohlednit také dvouosý ohyb. Osová únosnost a únosnost na vytažení se přitom uvažují pouze v příslušné rovině.

Literatura

[1]	Eurokód 5: Bemessung und Konstruktion von Holzbauten - Teil 1-1: Obecná pravidla – Společná pravidla a pravidla pro pozemní stavby; ČSN EN 1995-1-1:2006-12

Autor

Ing. Kuhn je zodpovědný za vývoj produktů pro dřevěné konstrukce a poskytuje technickou podporu zákazníkům.

Stahování

Model v programu RFEM

636 KB

;