Réponse:
Le ressort de rotation total se compose de plusieurs ressorts de rotation individuels, donnés dans [1] comme équation 10.11.
Dans le cas d'un maintien en rotation discontinu par pannes, RF-/STEEL EC3 prend en compte la rigidité en rotation due à la rigidité de l'assemblage CD,A, la rigidité en rotation CD,C due à la rigidité en flexion des pannes disponibles ainsi que la rigidité en rotation CD,B due à la déformation de la section, si elle est activée.
L’exécution de la connexion étant inconnue, la valeur infinie est définie par défaut. La rigidité du ressort de rotation est considérée comme une valeur réciproque 1/C, renseigner la valeur « infinie » donne une rigidité de ressort égale à 0. Un utilisateur connaissant la rigidité de ressort de rotation de l’assemblage peut entrer la valeur manuellement.
Le maintien en rotation CD,C est déterminé à partir de la rigidité en flexion selon la formule suivante :
| E | Module d’élasticité |
| k | Coefficient pour la position (travée interne, travée externe) |
| I | moment d'inertie Iy |
| s | Espacement entre poutres |
| e | Distance entre les pannes |
La rigidité en rotation CD,B due à la rigidité en flexion est déterminée selon la formule suivante, voir [3] et [4] :
| E | Module d’élasticité |
| tw | Épaisseur de l'âme de la ferme ou du composant supporté |
| G | Module G |
| h | Hauteur du treillis ou du composant supporté |
| tf | Épaisseur de la semelle du treillis |
| b | Largeur du treillis |
| e | Distance entre les pannes |
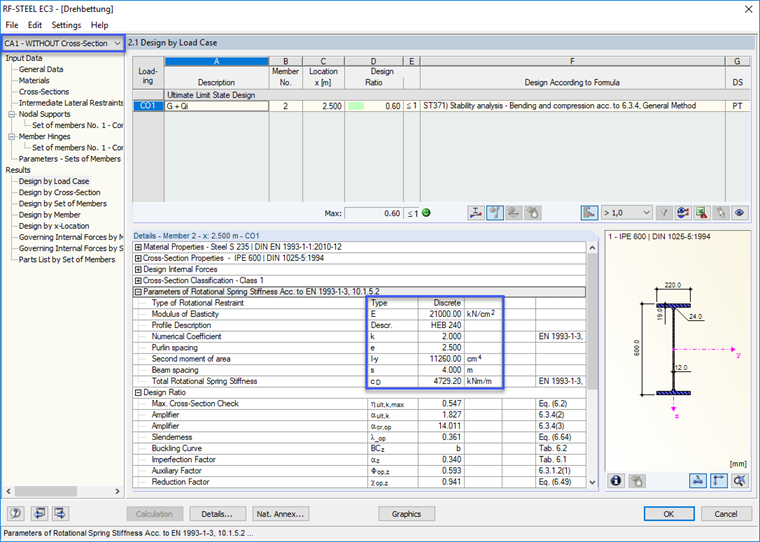
L’exemple ci-joint inclut deux cas de calcul.
Le cas 1 a été calculé sans considérer la déformation de la section. La rigidité totale du ressort en rotation est
CD = CD,C = 4729 kNm/m
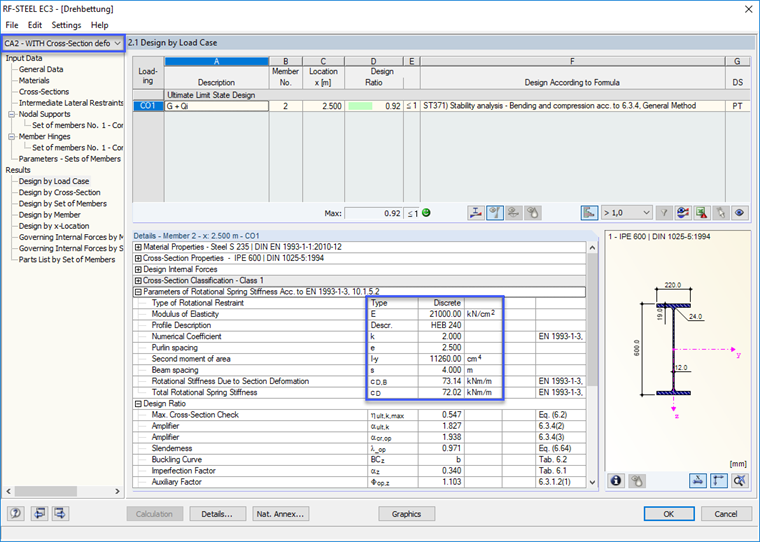
Le cas 2 a été calculé en considérant la déformation de la section. La rigidité totale du ressort en rotation est
CD = 72,02 kNm/m
Ressort simple CD,B = 73,14 kNm/m
Ressort simple CD,C = 4729 kNm/m
Ressort total :
