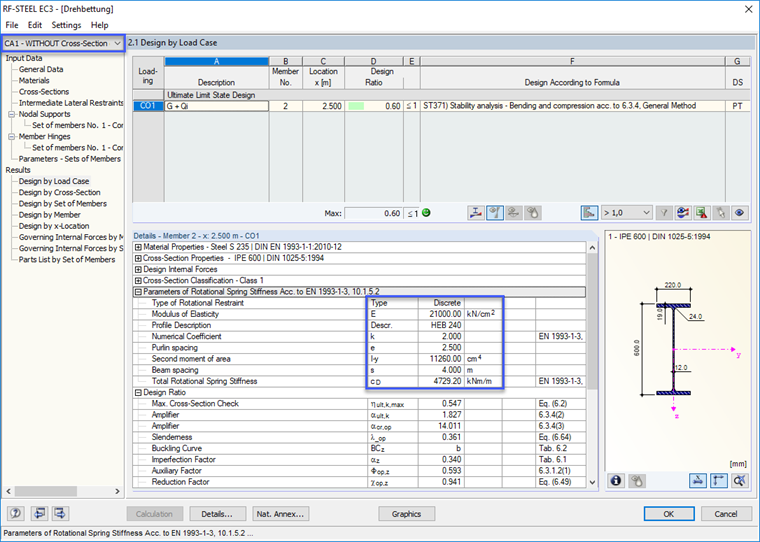
Celková rotační pružina se skládá z několika jednotlivých rotačních pružin, které jsou uvedeny v [1] pomocí rovnice 10.11.
Bei einer nicht kontinuierlichen Drehbettung durch Pfetten werden in RF-/STAHL EC3 die Drehbettung aus der Anschlusssteifigkeit CD,A, die Drehbettung CD,C aus der Biegesteifigkeit der aufliegenden Pfetten, sowie bei Aktivierung auch die Drehbettung CD,B aus Profilverformung berücksichtigt.
Da die Ausführung des Anschlusses unbekannt ist, wird hier standardmäßig ein unendlich großer Wert angesetzt. Die Federsteifigkeiten werden als Kehrwert 1/C berücksichtigt, somit ergibt "unendlich" eine Federsteifigkeit = 0. Kennt der Anwender die Drehfedersteifigkeit des Anschlusses, kann er diesen Wert manuell angeben.
Die Ermittlung der Drehbettung CD,C aus der Biegesteifigkeit erfolgt nach folgender Formel:
|
E |
E-Modul |
|
k |
Beiwert für Lage (Innenfeld, Außenfeld) |
|
I |
Trägheitsmoment Iy |
|
s |
Abstand der Riegel |
|
e |
Abstand der Pfetten |
Die Ermittlung der Drehbettung CD,B aus Profilverformung erfolgt nach folgender Formel, siehe [3] und [4]:
|
E |
E-Modul |
|
tw |
Stegdicke Binder bzw. gestütztes Bauteil |
|
G |
G-Modul |
|
h |
Höhe des Binders bzw. gestütztes Bauteil |
|
tf |
Flanschdicke des Binders |
|
b |
Breite Binder |
|
e |
Abstand der Pfetten |
Im angefügten Beispiel sind jeweils zwei Bemessungsfälle vorhanden.
Fall 1 wurde ohne Berücksichtigung der Profilverformung bemessen. Die Gesamtdrehfeder ergibt sich zu
CD = CD,C = 4729 kNm/m
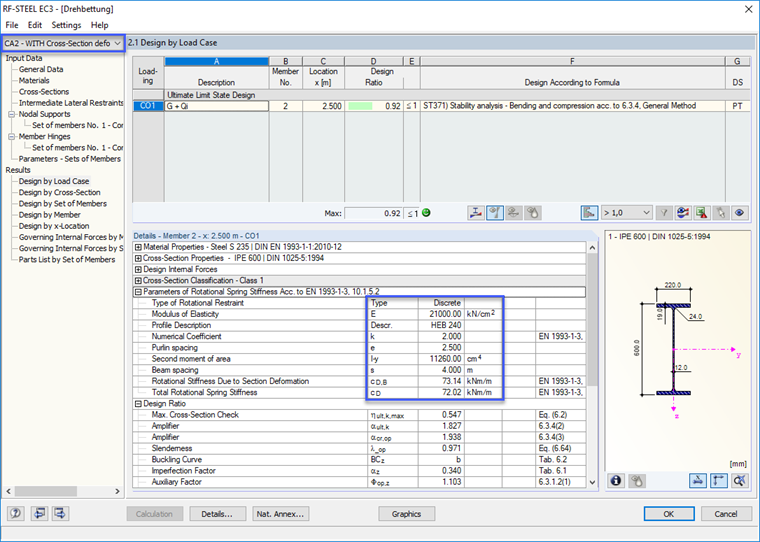
Fall 2 wurde unter Berücksichtigung der Profilverformung bemessen. Die Gesamtfeder ergibt sich zu
CD = 72,02 kNm/m
Einzelfeder CD,B = 73,14 kNm/m
Einzelfeder CD,C = 4729 kNm/m
Gesamtfeder: