Общие данные
Каждая узловая опора имеет свою собственную местную систему осей, которые означаются как X', Y' и Z'. В программе RFEM или RSTAB потом данная система по умолчанию основывается на общей системе осей модели. Тем не менее всегда можно задать пользовательскую систему осей или просто повернуть существующую. В нашем примере активировано отображение системы осей для всех узловых опор. Варианты отдельных нелинейностей для перемещений затем показаны в X'. Для других двух направлений осей опор применимы аналогичные действия.
Примечание: Нелинейность всегда относится к действующей опорной реакции.
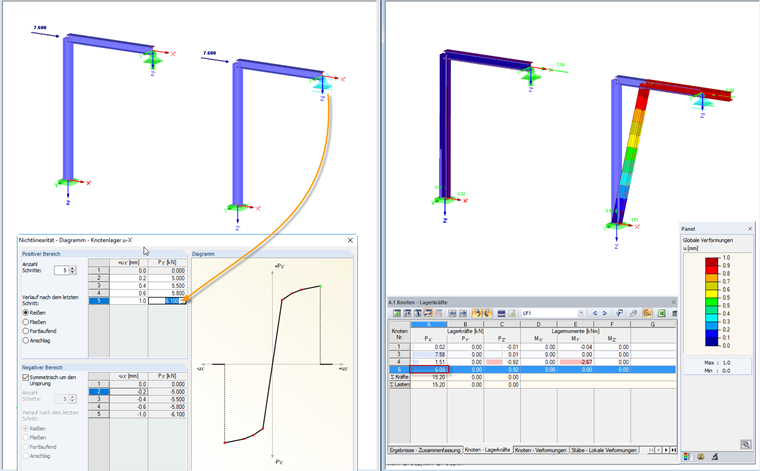
Диаграмма: Разрушение
В данной диаграмме можно воспроизвести довольно реалистичное у опоры взаимосвязь между нагрузками и деформациями. В случае «текучести» затем опора выходит из строя после достижения наибольшей положительной или наименьшей отрицательной опорной реакции. Положительные и отрицательные зоны могут быть определены также независимо друг от друга. На рисунке 01 действующая нагрузка была выбрана таким образом, чтобы представлять состояние незадолго до достижения разрыва.
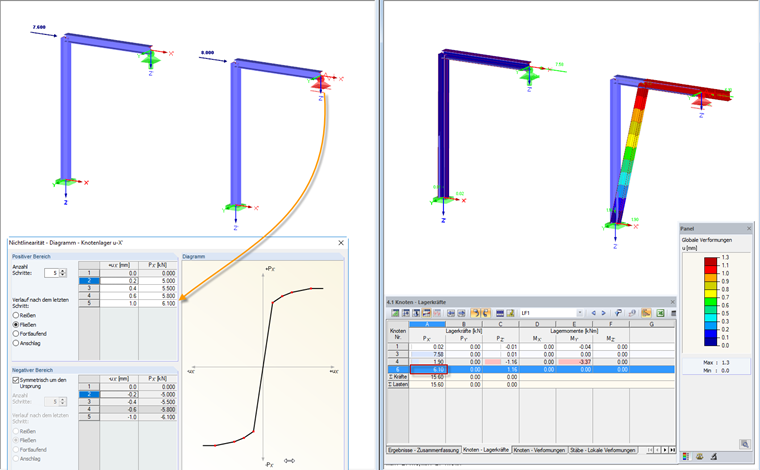
Диаграмма: Текучесть
В данном случае при достижении заданной деформации, опорная реакция даже при дальнейшем увеличении нагрузки уже не увеличивается. Это состояние называется «текучесть». Деформация может увеличиваться, но опорная сила не превышает заданного максимального значения. Это также можно задать по -разному для положительных и отрицательных зон.
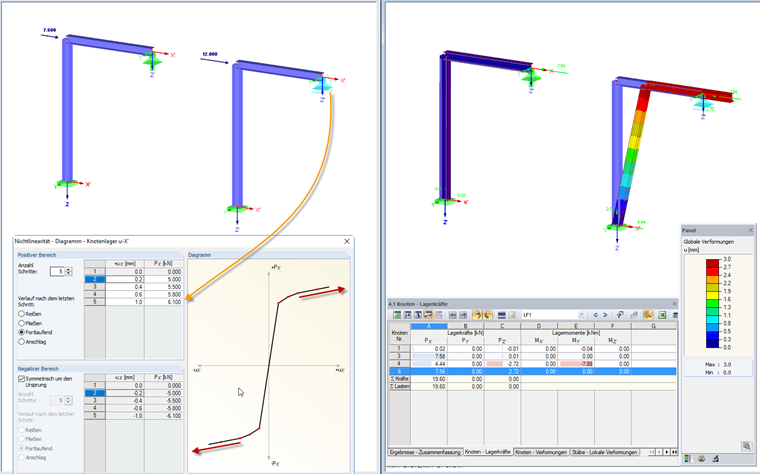
Диаграмма: Непрерывно
После достижения максимальной заданной деформации, опорная сила и деформация продолжают линейно увеличиваться. Отношение определяется градиентом прямой линии, описываемой двумя последними элементами диаграммы.
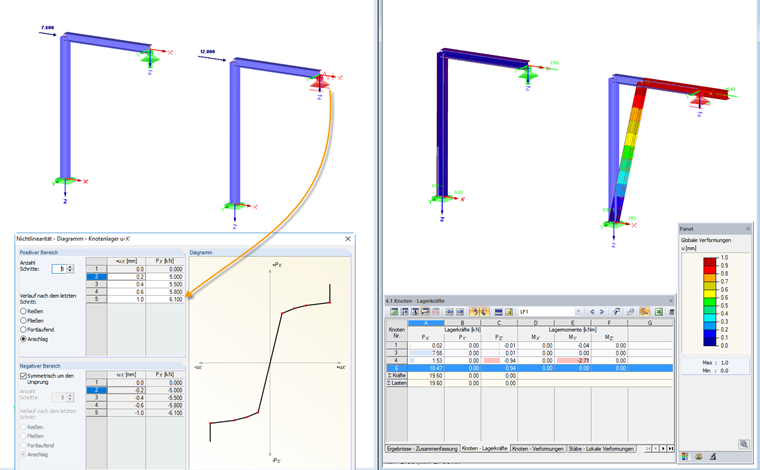
Диаграмма: Остановка
Начиная с деформации, превышающей последнее значение на диаграмме, эффект опоры является полным. Затем узел полностью сохраняется для заданного направления.
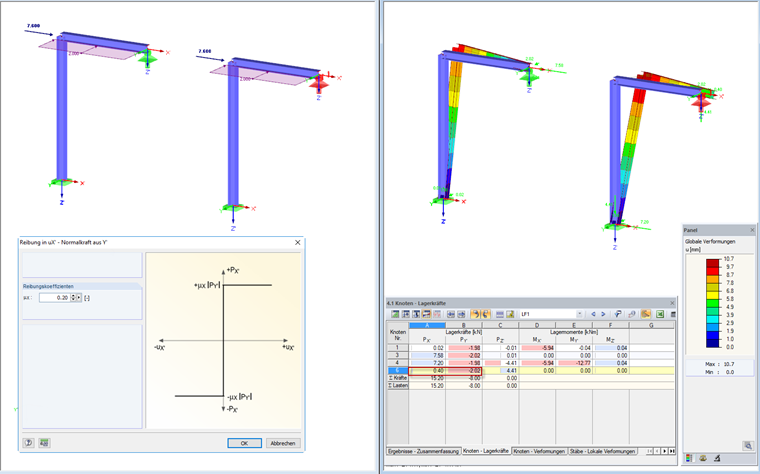
Трение PY'
В этом случае определение опоры учитывает опорную силу, действующую в направлении Y '. Определяя коэффициент трения, можно задать максимальное значение опорной силы в X ', относящееся к опорной силе в Y'.
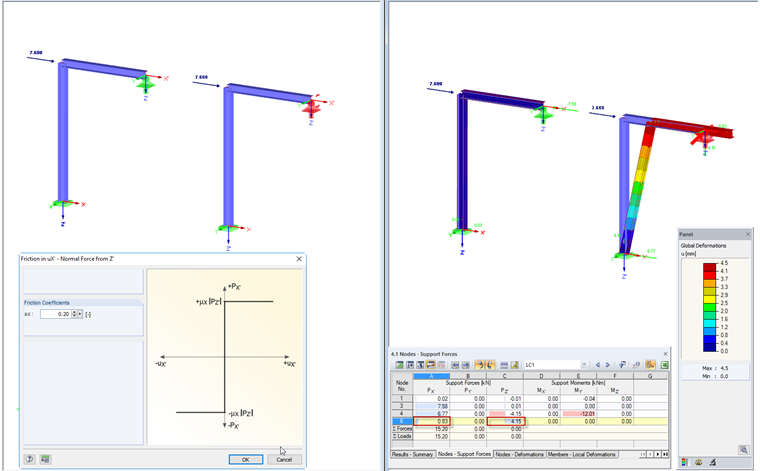
Трение PZ'
Определение опоры учитывает опорную силу, действующую в направлении Z '. Посредством определения коэффициента трения устанавливается максимальное значение опорной силы в X ', относящееся к опорной силе в Z'.
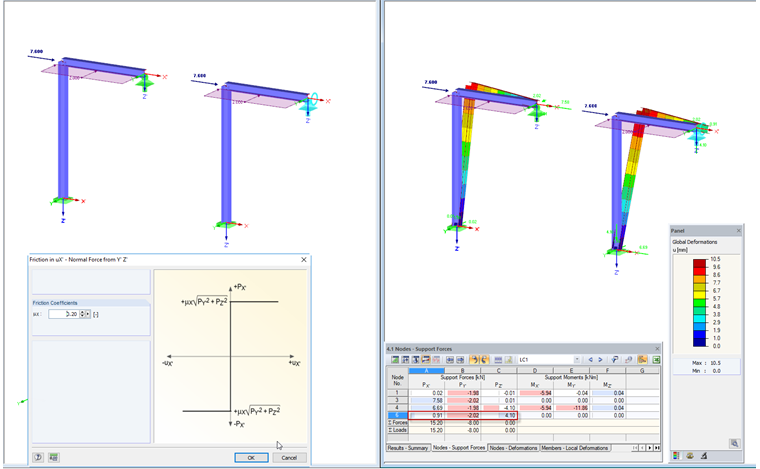
Трение PY'PZ '
Эта опция позволяет моделировать опору с помощью вектора PY 'и PZ', а также коэффициента трения.
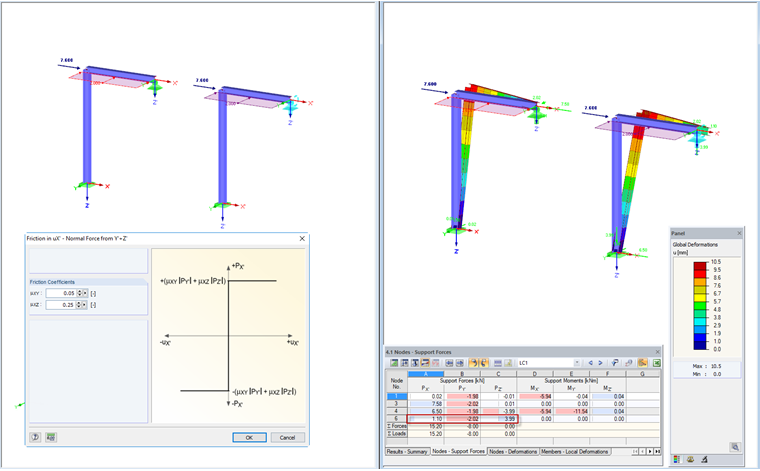
Трение PY'+ PZ'
Если опора спроектирована таким образом, что коэффициент трения для Y 'и Z' различен, можно использовать это определение опоры. Соответствующая опорная сила умножается на заданный коэффициент трения, и затем оба компонента складываются вместе, образуя управляющую опору в X '.