Obecně
Každá uzlová podpora má vlastní lokální osový systém. Osy se označují jako X', Y' a Z'. Standardně se lokální osový systém podpory řídí globálním systémem os v dané úloze v programu RFEM nebo případně RSTAB. Osový systém podpor však může definovat také sám uživatel nebo ho může jednoduše natočit. V našem příkladu zapneme zobrazení osových systémů u všech uzlových podpor. Jednotlivé možnosti zadání nelinearity si ukážeme v případě posunu ve směru X'. Obdobné možnosti ovšem platí i ve směru obou zbývajících os podpory.
Upozornění: Nelinearita se vždy vztahuje na působící podporovou sílu.
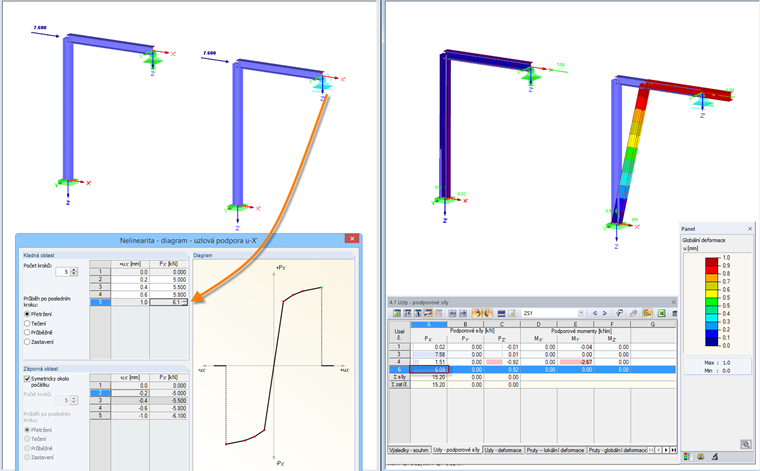
Diagram: Přetržení
Diagram umožňuje velice realisticky zachytit vztahy mezi zatížením a deformací podpory. Pokud zadáme „Přetržení“, bude podpora neúčinná po dosažení maximální kladné nebo minimální záporné podporové síly. Kladnou a zápornou oblast diagramu lze zadat také nezávisle na sobě. Na obr. 01 jsme zvolili působící zatížení tak, abychom znázornili stav krátce před přetržením.
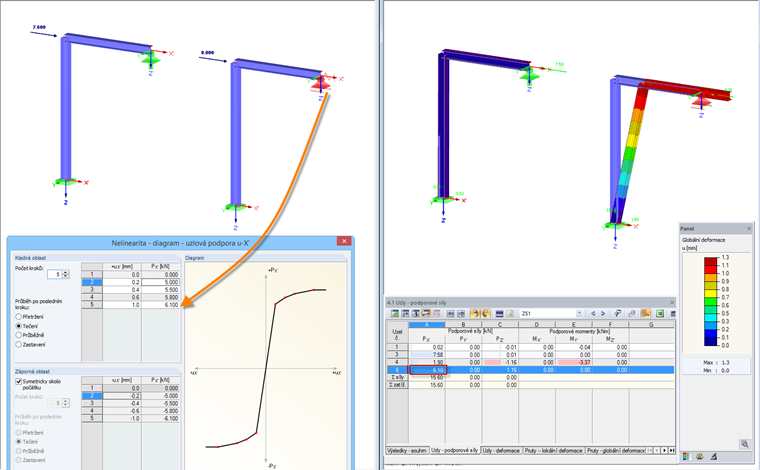
Diagram: Tečení
Po dosažení zadané deformace se podporová síla při dalším stupňování zatížení již dále nezvyšuje. Tento stav se označuje jako „Tečení“. Deformace může ještě růst, ovšem podporová síla nepřekročí zadanou maximální hodnotu. Nastavení lze opět zadat zvlášť pro kladnou a pro zápornou oblast.
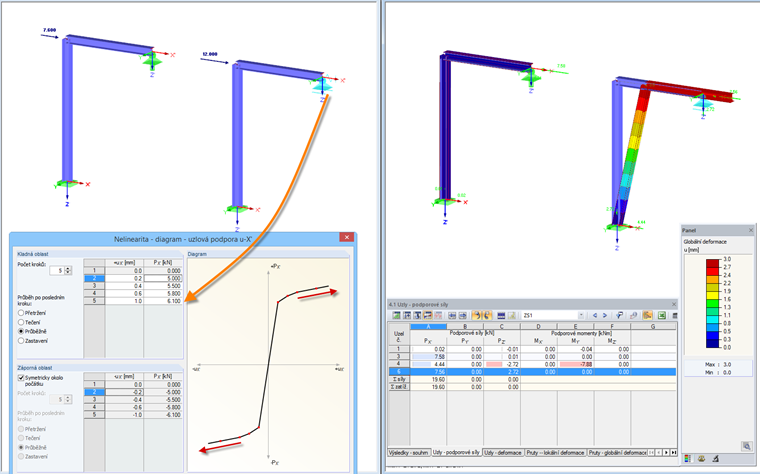
Diagram: Průběžně
Po dosažení zadané maximální deformace podporová síla i deformace dále lineárně rostou. Vztah se stanoví na základě sklonu přímky, který je dán dvěma posledními body diagramu.
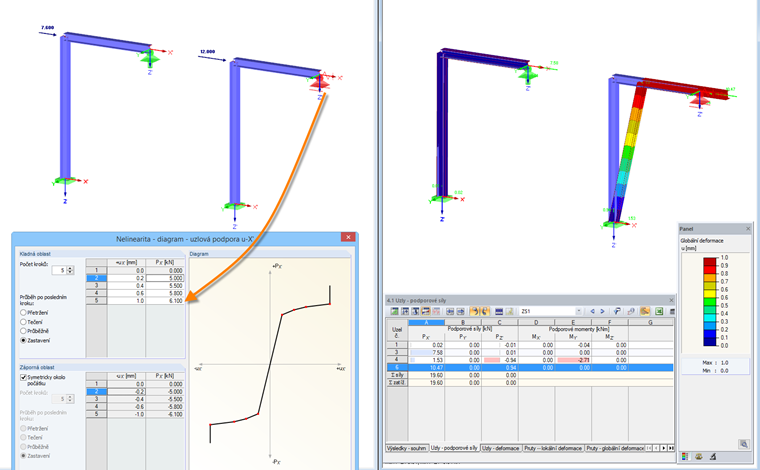
Diagram: Zastavení
Od určité deformace, která je větší než poslední hodnota v diagramu, je podpora plně účinná. Uzel je pak plně podepřen v zadaném směru.
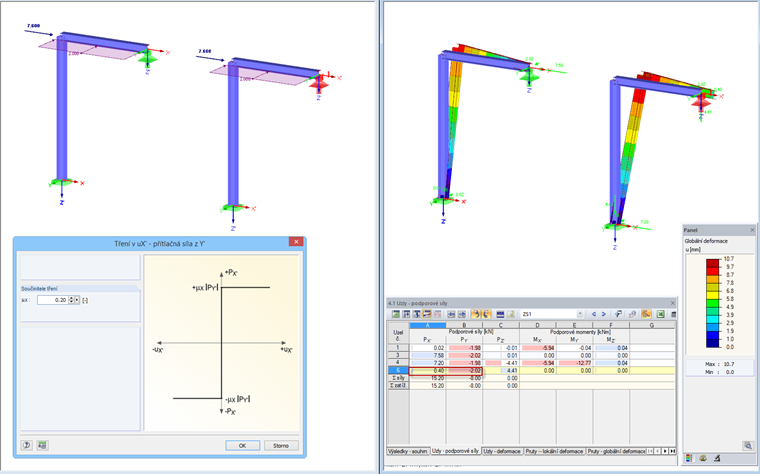
Tření PY'
V tomto případě se podpora zadá s ohledem na působící podporovou sílu ve směru Y'. Zadáním součinitele tření stanovíme vztah mezi maximální hodnotou podporové síly ve směru X' a podporovou silou ve směru Y'.
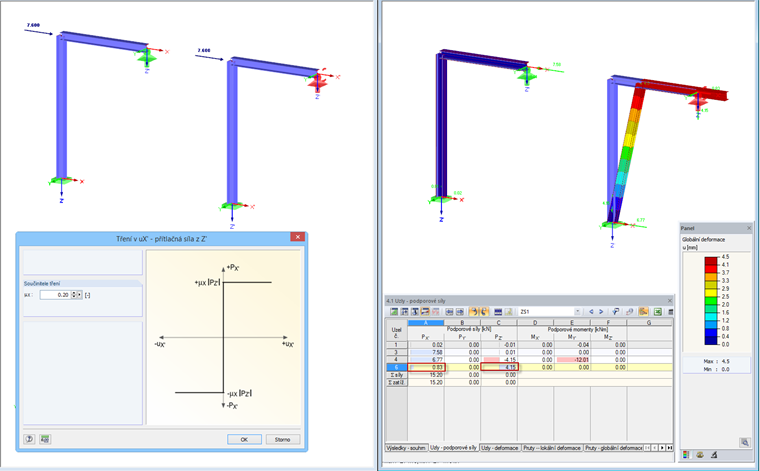
Tření PZ '
V tomto případě se podpora zadá s ohledem na působící podporovou sílu ve směru Z'. Zadáním součinitele tření stanovíme vztah mezi maximální hodnotou podporové síly ve směru X' a podporovou silou ve směru Z'.
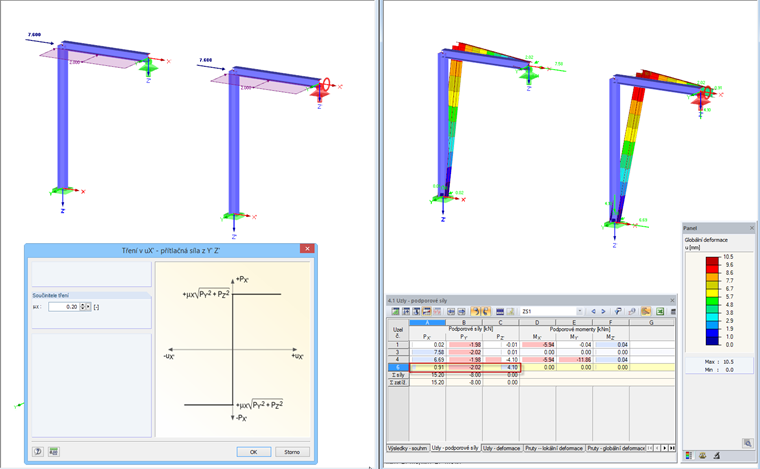
Tření PY'PZ'
Podpora je v tomto případě dána vektorem PY' a PZ' a společným součinitelem tření.
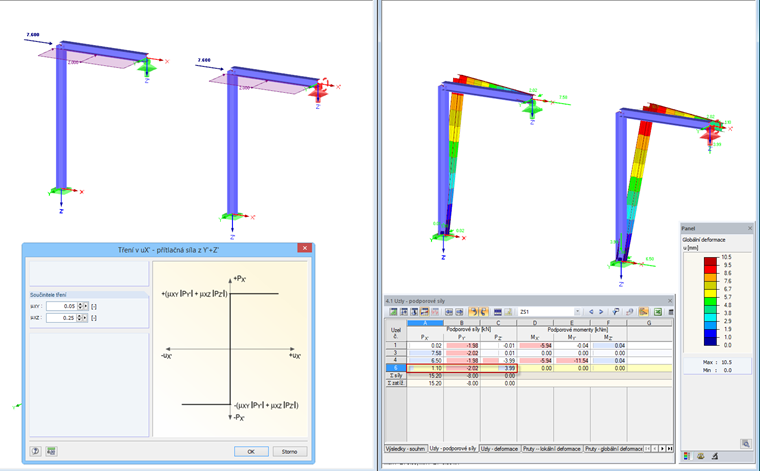
Tření PY'+PZ'
Jestliže mají pro směry Y' a Z' platit odlišné součinitele tření, pak můžeme použít tuto volbu. Příslušná podporová síla se vynásobí zadaným součinitelem tření. Následně se obě složky sečtou, a určí se tak rozhodující podepření ve směru X'.