Ten nieliniowy, ortotropowy, plastyczny model materiałowy umożliwia obliczanie i wymiarowanie konstrukcji murowych.
Jako metodę modelowania wybrano makromodelowanie muru. Oznacza to, że zachowanie murowanego materiału budowlanego, będącego kombinacją zaprawy murarskiej i cegieł, jest "rozmyte" na całej powierzchni.
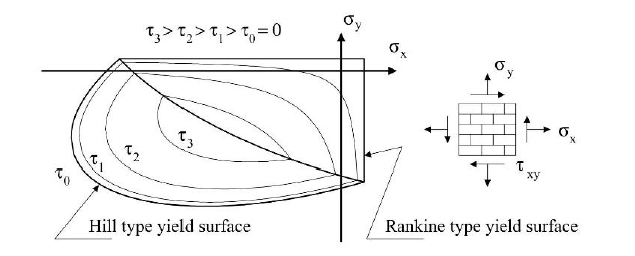
Na podstawie publikacji Lourenco (Lourenco 1996) wprowadzono model materiałowy składający się z dwóch powierzchni plastyczności (powierzchnia plastyczności Rankine'a Hilla). W projekcie badawczym DDMaD - Digitalizacja wymiarowania konstrukcji murowych - ten model materiałowy został zbadany i dalej rozwinięty, dzięki czemu w przypadku pomyślnego obliczenia przeprowadzane jest sprawdzenie podobne do Eurokodu.
Opis powierzchni uplastycznienia
Aby możliwe było realistyczne odwzorowanie zachowania materiału, wymagane parametry powierzchni plastyczności należy wyprowadzić z parametrów materiałowych.
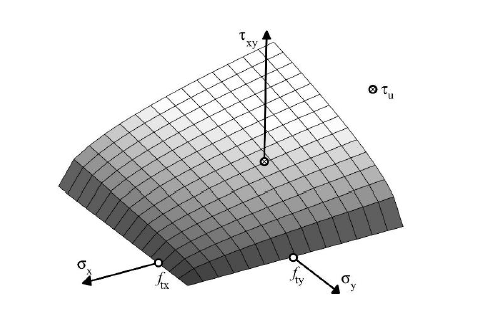
Definicja powierzchni Rankine'a
Powierzchnia Rankine'a definiowana jest przez trzy podstawowe parametry:
- ft⊥ = fty Wytrzymałość na rozciąganie prostopadle do spoiny w podporze
- ft||= ftx Wytrzymałość na rozciąganie równoległe do spoiny w podporze
- fvk0 = τxy Wytrzymałość na ścinanie w początku układu współrzędnych
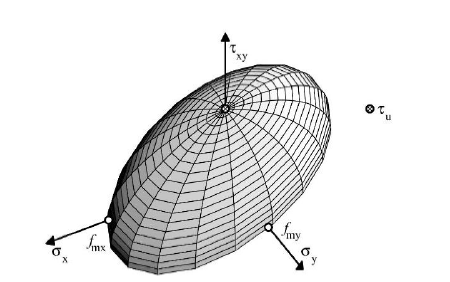
Definicja powierzchni wzgórza
Powierzchnia wzgórza jest definiowana przez cztery podstawowe parametry:
- fm⊥ = fmy Wytrzymałość na ściskanie prostopadle do spoiny w podporze
- fm||= fmx Wytrzymałość na ściskanie równolegle do spoiny w podporze
- Umowna wytrzymałość na ścinanie w początku układu współrzędnych
- Wytrzymałość na ściskanie dwukierunkowe
Parametry powierzchni wzgórza Rankine'a
Aby możliwe było realistyczne opisanie materiału murowego lub kombinacji zaprawa-cegła w modelu materiałowym, wymagane są dodatkowe parametry α,β,γ.