This nonlinear, orthotropic plastic material model allows for the calculation and design of masonry.
Macro-modeling of the masonry is chosen as the modeling approach. This means that the behavior of the masonry building material, which consists of a combination of mortar and bricks, is displayed as "blurred" over the surface.
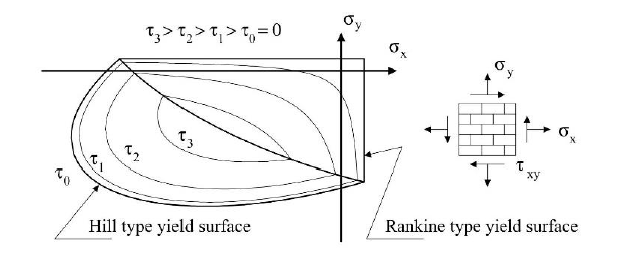
Based on the publications by Lourenco (Lourenco 1996), the material model consisting of two yield surface functions (Rankine Hill yield surface) was implemented. In the research project DDMaD (Digitizing the Design of Masonry Stuctures), this material model was examined and further developed, so a design check similar to Eurocode is carried out in the case of a successful calculation.
Description of Yield Surfaces
In order to be able to represent realistic material behavior, it is necessary to derive the required parameters of the yield surface from the material parameters.
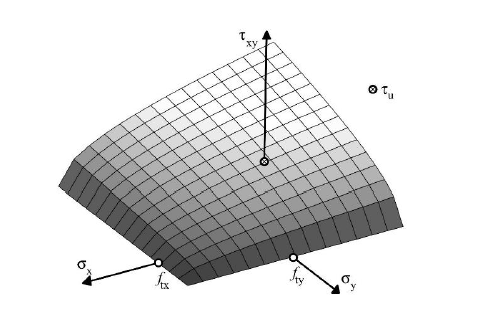
Definition of Rankine Surface
A Rankine surface is defined by three essential parameters:
- ft⊥ = fty Tensile strength normal to the interstice of a support
- ft|| = ftx Tensile strength parallel to the interstice of a support
- fvk0 = τxy Shear strength in the coordinate origin
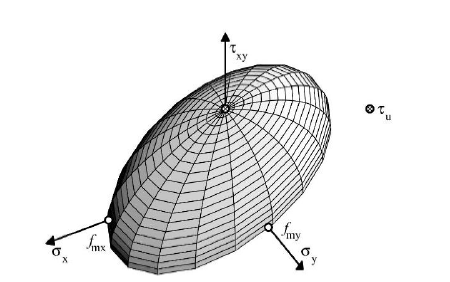
Definition of Hill Surface
A Hill surface is defined by four essential parameters:
- fm⊥ = fmy Compressive strength normal to the interstice of a support
- fm|| = fmx Compressive strength parallel to the interstice of a support
- Notional shear strength in the coordinate origin
- Biaxial compressive strength
Parameters of Rankine Hill Surface
In order to be able to describe the masonry material or the mortar-brick combination realistically in the material model, additional parameters α,β,γ are necessary.