Как часть линейного вычисления собственных чисел с помощью надстройки «Устойчивость конструкции», «Коэффициенты модальной релевантности» (MRF) теперь также отображаются для всех форм колебаний и отдельных стержней в дополнение к критическим нагрузкам и эквивалентным эффективным длинам, определенным на основе этих нагрузок. MRF качественно описывает соответствие стержня расчетной форме колебаний. Расчет основан на энергии упругой деформации, которая получается для каждого отдельного стержня ( k ) в форме колебаний ( i ). Поскольку формы колебаний можно масштабировать по мере необходимости, абсолютные энергии деформации не учитываются. Вместо этого энергии всех отдельных элементов соотносятся друг с другом:
где
- ui - форма колебаний для собственного числа i
- Kek - матрица жесткости элемента для стержня k
MRF, равный 100%, означает, что отдельный стержень имеет максимальное значение для рассматриваемой собственной моды. Однако стержни, которые по сравнению с ними не имеют значительной энергии деформации, не представляют интереса для рассматриваемой формы колебаний.
Как часть оценки устойчивости по форме колебаний, MRF можно использовать для быстрого и систематического различения местных и общих форм колебаний. Если несколько отдельных стержней имеют значительную MRF для собственной моды (например, более 20%), это указывает на нестабильность всей конструкции или ее части. С другой стороны, если сумма всех MRF для собственной моды составляет около 100%, следует ожидать явления местной устойчивости (например, потери устойчивости одного стержня).
Кроме того, MRF можно использовать для определения решающих критических нагрузок и эквивалентных эффективных длин определенных стержней (например, для расчета устойчивости). Здесь рекомендуется поэлементная оценка результатов анализа. Формами колебаний, для которых стержень имеет небольшие значения MRF (например, менее 20%), можно легко пренебречь при поиске критической эффективной длины стержня.
Пример
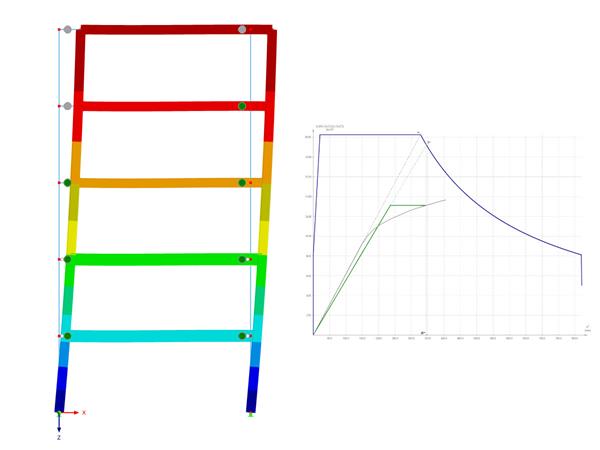
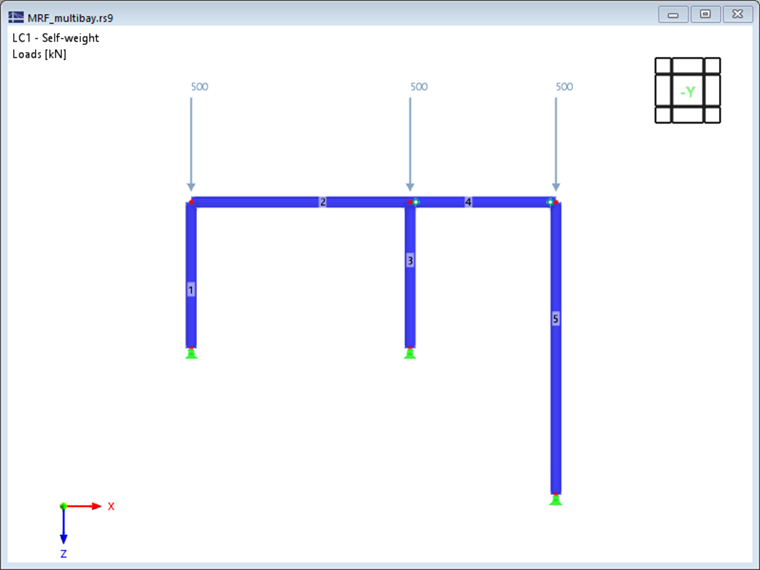
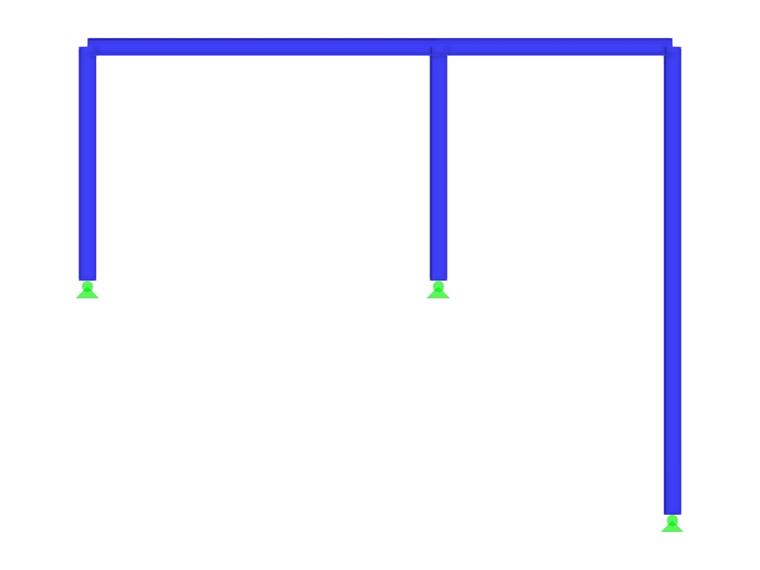
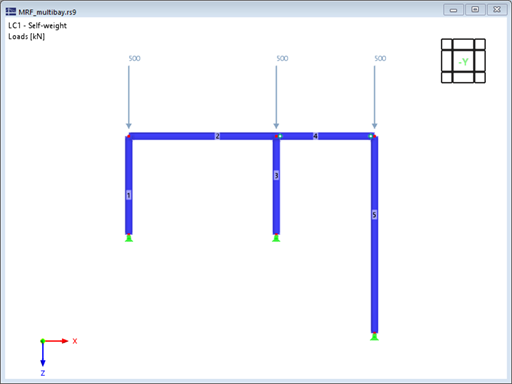
Далее значение MRF демонстрируется на простом примере. Двухшарнирная рама с отдельной штыревой колонной (правая колонна) рассматривается в плоскости, как показано на рисунке 1. Для отображенного напряжения выполняется линейный расчет устойчивости с применением настроек по умолчанию.
Оценка форм колебаний инженерными экспертами
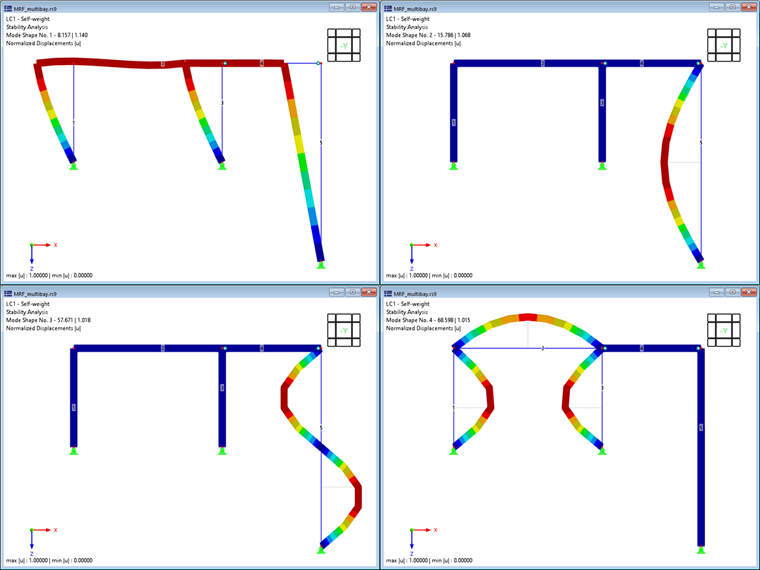
Первые четыре формы колебаний конструкции показаны на рисунке 2; их можно охарактеризовать следующим образом:
- Форма первой моды характеризуется боковой неустойчивостью каркаса. Элементы 4 и 5 с штифтами на концах показывают большие смещения, но следуют только за боковым перемещением рамы, так что в этих элементах не возникает значительной энергии деформации.
- Однако формы колебаний 2 и 3 можно определить как отдельные формы потери устойчивости колонны с штырями (стержень 5). Рама обеспечивает боковую опору оголовка колонны, так что устойчивость ' колонны также может быть идеализирована как форма потери устойчивости по Эйлеру II (форма первой и второй колебаний вокруг главной оси).
- В четвертой форме колебаний наблюдается потеря устойчивости более коротких колонн, принадлежащих двухшарнирной раме. Однако, как и в первой собственной моде, жестко соединенный транец способствует увеличению критической нагрузки.
Объективный анализ с помощью MRF
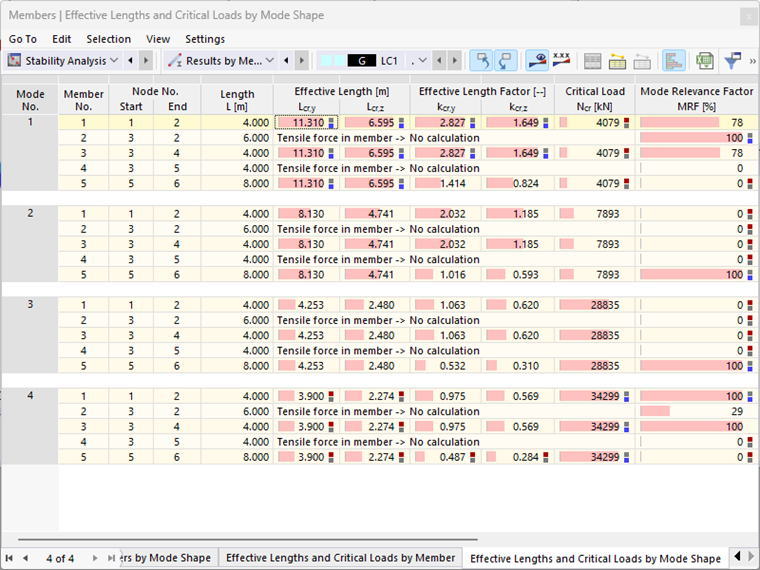
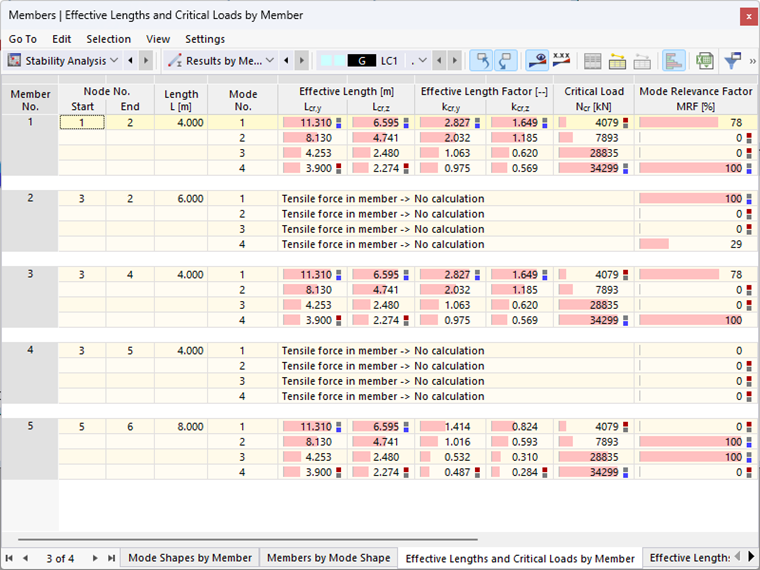
В дополнение к «ручному» анализу и оценке формы колебаний, пользователь теперь имеет в своем распоряжении объективный вспомогательный фактор. На рисунке 3 показана таблица результатов «Эффективные длины и критические нагрузки по форме колебаний» для системы-примера. Коэффициенты соответствия модам, рассчитанные стержнем, подтверждают, что в формах колебаний 1 и 4 преобладает жесткая рама (элементы 1-3), в то время как подвешенные элементы 4 и 5 не имеют отношения (MRF = 0%). В отличие от этого, только стержень 5 (MRF = 100%) участвует в формах колебаний 2 и 3 - быстрый взгляд на таблицу результатов показывает, что эти формы колебаний должны быть местным нарушением устойчивости.
Поэлементное представление модальных коэффициентов релевантности (см. Рисунок 4) подходит для определения определяющих эффективных длин и критических нагрузок отдельных стержней. Выбранный пример представляет собой плоскую конструктивную систему; отклонение от плоскости каркаса (вокруг оси второстепенного стержня) невозможно из-за выбранных основных настроек. Таким образом, только сильная ось (y-) важна здесь для анализа определяющих эффективных длин и критических нагрузок.
Результаты, показанные на рисунке 4, подразумевают, что первая форма колебаний должна быть применена в расчете устойчивости опор рамы (стержни 1 и 3). Из собственных форм, в которых участвуют стойки каркаса (1 и 4), нагрузка на разветвление здесь минимальна. Для расчета потери устойчивости вокруг главной оси с помощью метода эквивалентных стержней следует выбрать коэффициент длины потери устойчивости 2,827. Однако для маятниковой колонны (стержень 5) собственная мода 2 с коэффициентом эффективной длины 1,016 будет определяющей. Самая низкая критическая нагрузка также рассчитывается здесь для формы колебаний 1, но маятниковая колонна не участвует в этой форме колебаний (MRF = 0%).
Чтобы сделать табличный анализ MRF более четким, рекомендуется отфильтровать все MRF до определенного предельного значения (например, менее 20%) с помощью «Менеджера таблиц результатов».
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
