Při lineárním výpočtu vlastních čísel pomocí addonu Stabilita konstrukce se nyní kromě kritických zatížení a z nich stanovených náhradních vzpěrných délek zobrazují také "modální součinitele důležitosti" (Modal Relevance Factors - MRF) pro všechny vlastní tvary a jednotlivé pruty. MRF kvalitativně popisuje podíl účasti prutu ve vypočítaném vlastním tvaru. Při výpočtu se vychází z elastické deformační energie, která připadá na každý jednotlivý prut k vlastního tvaru i. Vzhledem k tomu, že měřítko vlastních tvarů lze libovolně měnit, neuvažují se žádné absolutní deformační energie. Místo toho jsou energie všech jednotlivých prutů shrnuty do vzájemného poměru:
| ui | Vlastní tvar pro vlastní číslo i |
| kek | Matice tuhosti prvku pro prut k |
kde
- ui - vlastní tvar pro vlastní číslo i
- Kek - matice tuhosti prvku pro prut k
MRF 100 % znamená, že jednotlivý prut má pro uvažovaný vlastní tvar maximální důležitost. Pruty, které nemají v porovnání žádnou významnou deformační energii, jsou naproti tomu pro uvažovaný vlastní tvar nedůležité.
V rámci stabilitní analýzy vlastních tvarů lze pomocí MRF rychle a systematicky rozlišovat mezi lokálními a globálními tvary. Pokud je několik jednotlivých prutů důležitých pro vlastní tvar (MRF je např. větší než 20 %), ukazuje to na nestabilitu celé nebo dílčí konstrukce. Pokud se na druhé straně součet všech MRF pro vlastní tvar pohybuje okolo 100 %, je třeba počítat s lokálním stabilitním jevem (např. vybočení jednotlivého prutu).
Kromě toho lze pomocí MRF stanovit rozhodující kritická zatížení a náhradní vzpěrné délky určitých prutů (např. pro posouzení stability). Pro to program nabízí vyhodnocení výsledků analýzy po prutech. Vlastní tvary, v nichž má prut malé hodnoty MRF (např. menší než 20 %), lze při hledání kritické vzpěrné délky prutu snadno zanedbat.
Příklad použití
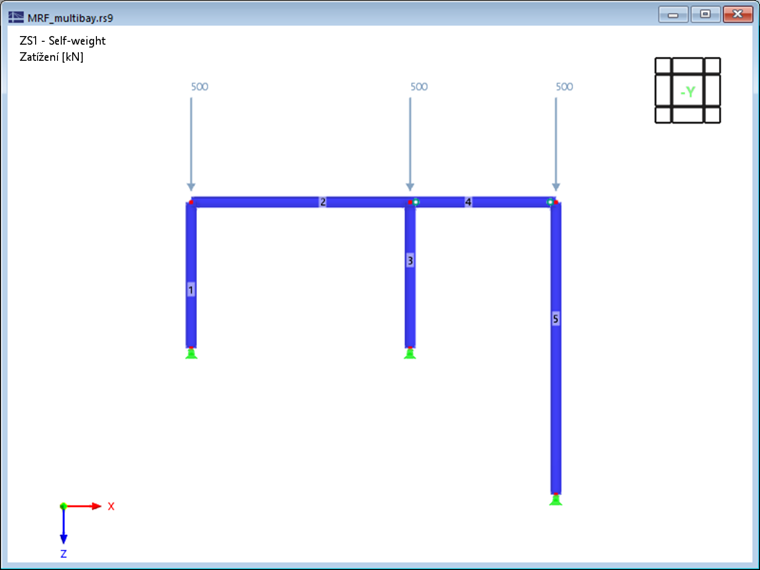
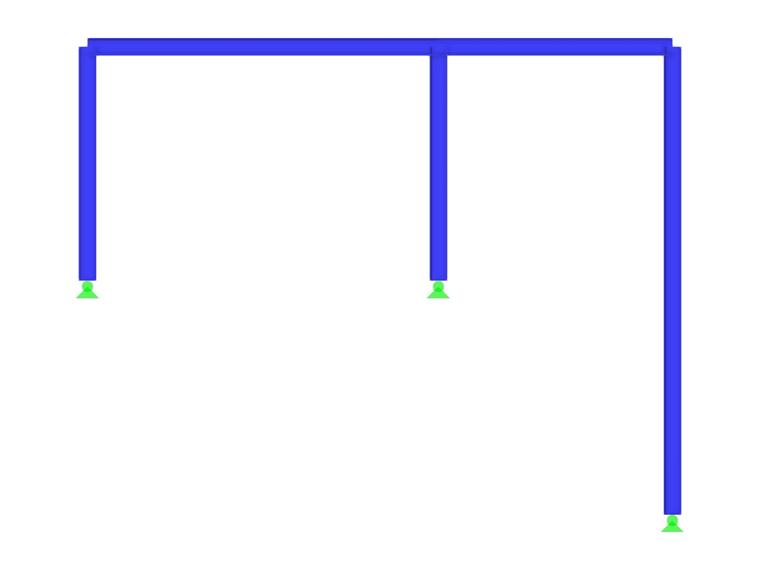
V následujícím textu je předveden význam MRF na jednoduchém příkladu. Dvoukloubový rám s kloubově připojeným sloupem v rovině je znázorněn na obrázku 1. Pro zobrazené zatížení se provede lineární posouzení stability s použitím standardního nastavení.
Inženýrsko-technické vyhodnocení vlastních tvarů
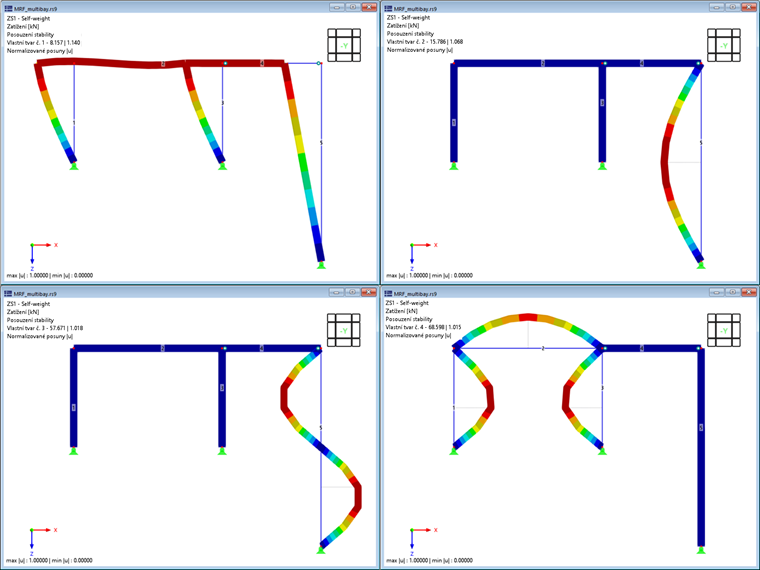
První čtyři vlastní tvary konstrukce jsou znázorněny na obrázku 2; lze je charakterizovat následovně:
- První vlastní tvar je charakterizován vybočením rámu do strany. Kloubově připojené pruty 4 a 5 vykazují sice velké posuny, ale následují pouze boční pohyb rámu, takže v těchto prutech nevzniká žádná významná deformační energie.
- Vlastní tvary 2 a 3 lze naproti tomu označit jako tvary izolovaného vybočení kloubově připojeného sloupu (prutu 5). Rám zajišťuje boční podepření horního konce sloupu, takže stabilitu sloupu lze idealizovat také jako II. typ Eulerova vzpěru (první a druhý vlastní tvar okolo hlavní osy s největší tuhostí).
- Ve čtvrtém vlastním tvaru lze pozorovat vybočení kratších sloupů dvoukloubového rámu. Stejně jako v prvním vlastním tvaru však přispívá ohybově pevně připojený nosník ke zvýšení kritického vzpěrného zatížení.
Objektivní analýza pomocí MRF
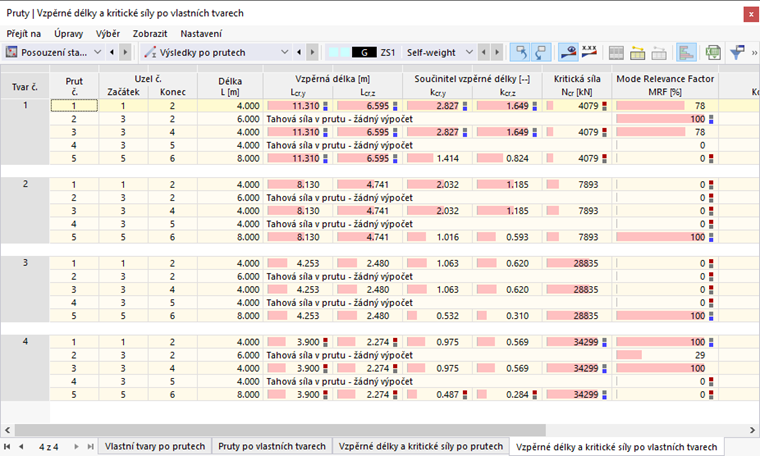
Kromě "ruční" analýzy a vyhodnocení vlastních tvarů má nyní uživatel k dispozici objektivní pomocný součinitel v podobě MRF. Na obrázku 3 je výsledková tabulka "Vzpěrné délky a kritické síly po vlastních tvarech" pro náš příklad. Modální součinitele důležitosti vypočítané pro daný prut potvrzují, že vlastním tvarům 1 a 4 dominuje tuhý rám (pruty 1-3), zatímco kloubově připojené pruty 4 a 5 nemají žádnou důležitost (MRF = 0 %). Naproti tomu u vlastních tvarů 2 a 3 se na deformační energii podílí pouze prut 5 (MRF = 100 %) - letmý pohled do tabulky výsledků ukazuje, že u těchto vlastních tvarů se musí jednat o lokální porušení stability.
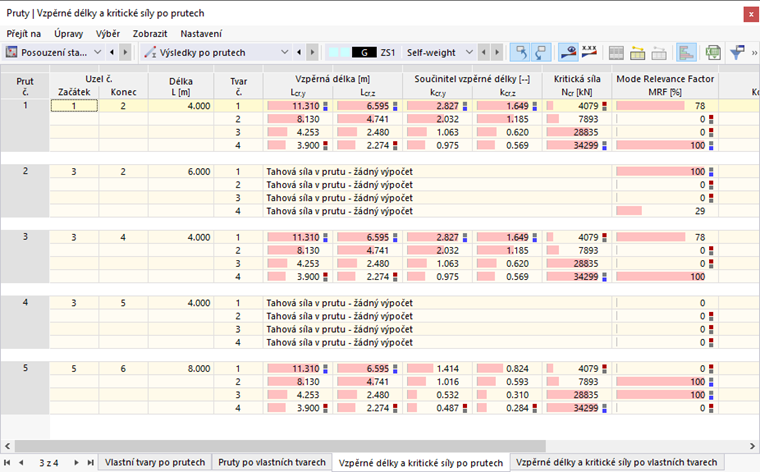
Pro stanovení rozhodujících vzpěrných délek a kritických zatížení jednotlivých prutů se hodí zobrazení modálních součinitelů důležitosti po prutech (viz obrázek 4). Vybraný příklad představuje rovinný konstrukční systém; výchylka z roviny rámu (okolo hlavní osy prutu s nejmenší tuhostí) není na základě zvolených základních nastavení možná. Pro výpočet rozhodujících vzpěrných délek a kritických zatížení zde tak hraje roli pouze hlavní osa největší tuhosti (y).
Z výsledků na obrázku 4 vyplývá, že při stabilitní analýze rámových sloupů (pruty 1 a 3) by měl být použit první vlastní tvar. Z vlastních tvarů, kterých se účastní rámové sloupy (1 a 4), je kritické zatížení minimální zde. Pro posouzení vzpěru okolo hlavní osy největší tuhosti metodou náhradního prutu je třeba zvolit součinitel vzpěrné délky 2,827. Pro kloubově připojený sloup (prut 5) je naproti tomu rozhodující vlastní tvar 2 se součinitelem vzpěrné délky 1,016. Nejnižší kritické zatížení se zde sice počítá také pro vlastní tvar 1, ale kloubově připojený sloup se na tomto tvaru nepodílí (MRF = 0 %).
Pro lepší přehlednost analýzy MRF v tabulce se doporučuje odfiltrovat všechny MRF do určité mezní hodnoty (např. méně než 20%) pomocí "Správce výsledkových tabulek".