Como parte del cálculo de valores propios lineales utilizando el complemento Estabilidad de la estructura, ahora también se muestran los "Factores de relevancia modal" (MRF) para todas las deformadas del modo y barras individuales, además de las cargas críticas y las longitudes eficaces equivalentes determinadas a partir de estas cargas. Der MRF beschreibt qualitativ die Relevanz eines Stabes für eine berechnete Eigenform. Die Berechnung erfolgt auf Grundlage der elastische Verformungsenergie, die sich für jeden Einzelstab k in der Eigenform i ergibt. Da die Eigenformen beliebig skalierbar sind, werden keine absoluten Verformungsenergien betrachten. Stattdessen werden die Energien aller Einzelstäbe miteinander ins Verhältnis gesetzt:
| ui | Deformada del modo para el valor propio i |
| kek | Matriz de rigidez del elemento para la barra k |
Donde
- ui - Eigenform für Eigenwert i
- Kek - Elementsteifigkeitsmatrix für Stab k
Ein MRF von 100 % bedeutet also, dass ein Einzelstab maximale Relevanz für die betrachtete Eigenform besitzt. Stäbe, die im Vergleich keine signifikante Verformungsenergie aufweisen, sind für die betrachtete Eigenform dagegen nicht von Interesse.
Im Rahmen der eigenformweisen Auswertung der Stabilitätsanalyse kann der MRF herangezogen werden, um schnell und systematisch zwischen lokalen und globalen Eigenformen zu unterscheiden. Weisen mehrere Einzelstäbe für eine Eigenform signifikante MRF (z. B. größer 20 %) auf, deutet dies auf eine Instabilität der Gesamt- oder einer Teilstruktur hin. Liegt die Summe aller MRF für eine Eigenform hingegen bei etwa 100 %, ist ein lokales Stabilitätsphänomen (z. B. Knicken eines Einzelstabes) zu erwarten.
Außerdem kann der MRF genutzt werden, um maßgebende Verzweigungslasten und äquivalente Knicklängen bestimmter Stäbe (z. B. für die Stabilitätsbemessung) zu bestimmen. Hierfür bietet sich die stabweise Auswertung der Analyseergebnisse an. Eigenformen, für die der Stab kleine MRF-Werte (z. B. kleiner 20 %) besitzt, können auf der Suche nach der kritischen Knicklänge des Stabes ohne Weiteres vernachlässigt werden.
Ejemplo
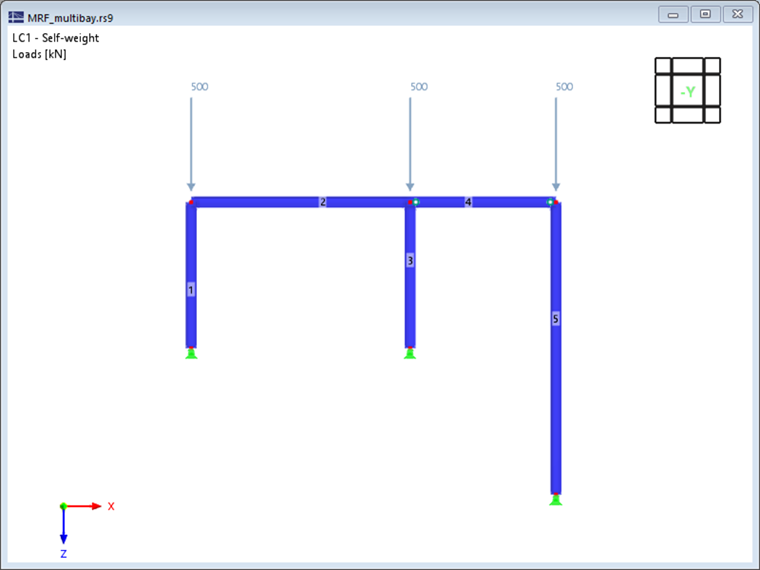
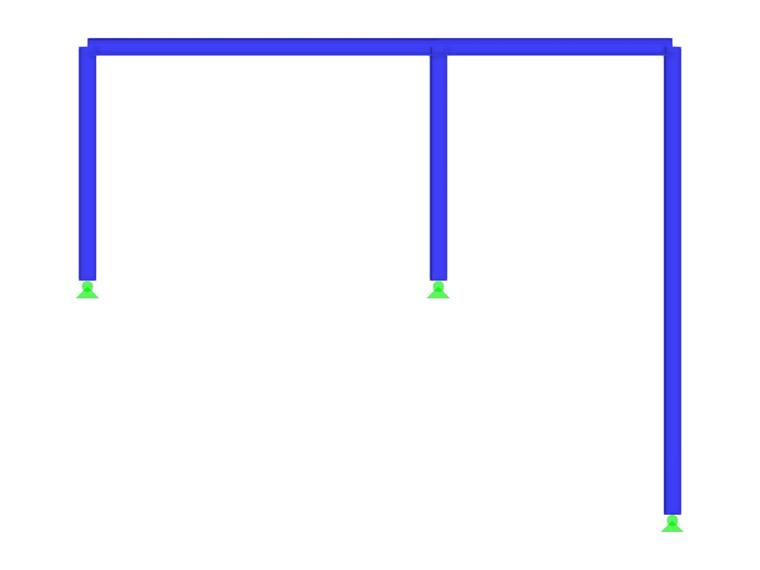
Im Folgenden wird die Bedeutung des MRF anhand eines simplen Beispiels demonstriert. Betrachtet wird ein Zweigelenkrahmen mit angependelter Einzelstütze in der Ebene entsprechend Bild 1. Für die dargestellte Beanspruchung wird eine lineare Stabilitätsanalyse mit den Standardeinstellungen durchgeführt.
Ingenieurstechnische Bewertung der Eigenformen
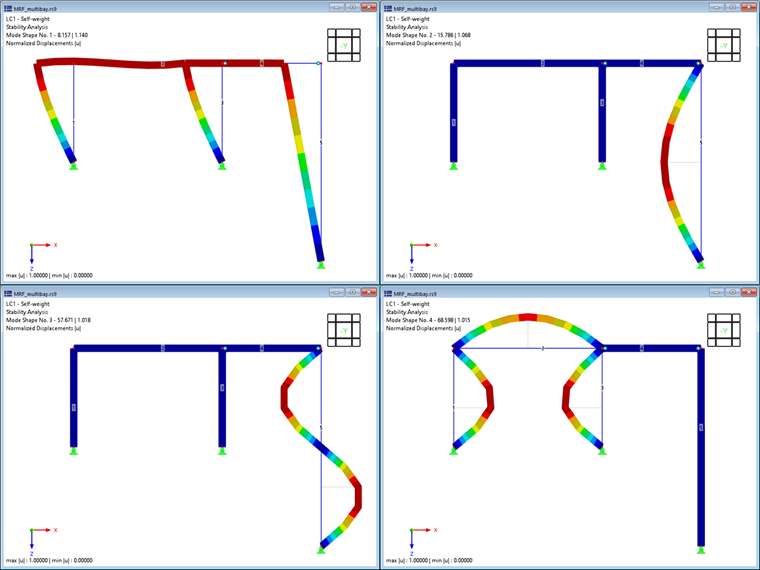
Die ersten vier Eigenformen der Struktur sind in Bild 2 dargestellt, sie können wie folgt charakterisiert werden:
- Die erste Eigenform ist durch das seitliche Ausweichen des Rahmens geprägt. Die angependelten Stäbe 4 und 5 weisen zwar große Verschiebungen auf, folgen aber lediglich der seitlichen Bewegung des Rahmens, sodass keine signifikante Verformungsenergie in diesen Stäben entsteht.
- Die Eigenformen 2 und 3 können hingegen als isolierte Knickfiguren der angependelten Stütze (Stab 5) identifiziert werden. Der Rahmen sorgt für eine seitliche Halterung des Stützenkopfes, sodass die Stabilität der Stütze auch als Eulerfall II (erste und zweite Eigenform um die starke Achse) idealisiert werden kann.
- Die vierte Eigenform zeigt wieder ein Ausknicken der Rahmenstiele. Der biegesteif angeschlossene Riegel trägt hier allerdings, wie in der ersten Eigenform, zu einer Erhöhung der Verzweigungslast bei.
Objektive Analyse mittels MRF
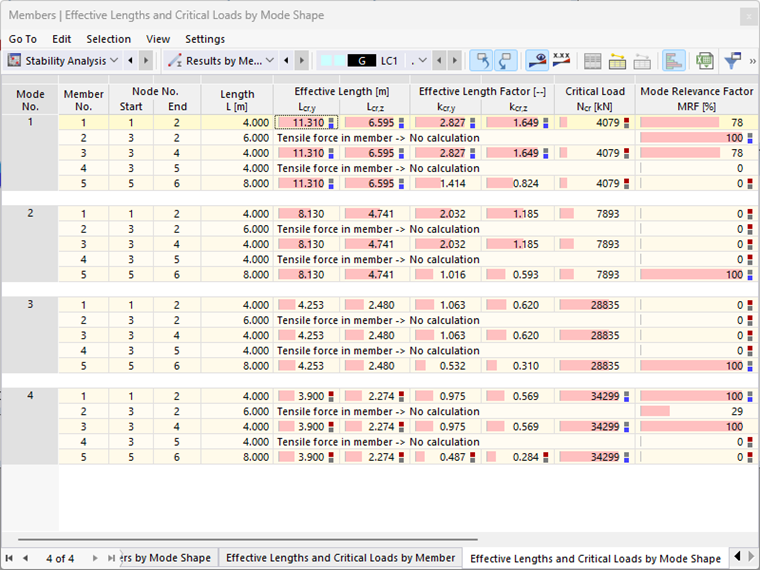
Neben der „händischen“ Überprüfung und Bewertung der Eigenformen steht dem Nutzer mit dem MRF nun eine objektive Hilfsgröße zur Verfügung. In Bild 3 ist die Ergebnistabelle „Knicklängen und Verzweigungslasten eigenformweise“ für das Beispielsystem dargestellt. Die stabweise berechneten modalen Relevanzfaktoren bestätigen, dass die Eigenformen 1 und 4 durch den biegesteifen Rahmen (Stäbe 1-3) dominiert werden, während die angependelten Stäbe 4 und 5 keinerlei Relevanz besitzen (MRF = 0 %). An den Eigenformen 2 und 3 beteiligt sich hingegen nur Stab 5 (MRF = 100 %) – ein kurzer Blick auf die Ergebnistabelle offenbart, dass es sich bei diesen Eigenformen also um ein lokales Stabilitätsversagen handeln muss.
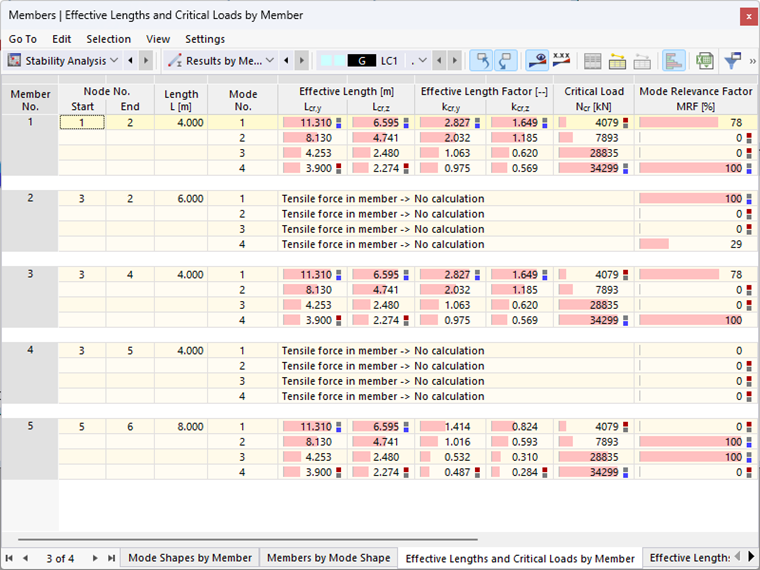
Die stabweise Darstellung der Modalen Relevanzfaktoren (siehe Bild 4) eignet sich zur Bestimmung der maßgebenden Knicklängen und Verzweigungslasten der Einzelstäbe. Bei dem gewählten Beispiel handelt es sich um ein ebenes System, ein Ausweichen aus der Rahmenebene (um die schwache Stabachse) ist aufgrund der gewählten Basiseinstellungen nicht möglich. Für die Analyse der maßgebenden Knicklängen und Verzweigungslasten ist hier also nur die starke (y-) Achse von Bedeutung.
Die in Bild 4 dargestellten Ergebnisse implizieren, dass für eine Stabilitätsanalyse der Rahmenstiele (Stäbe 1 und 3) die erste Eigenform anzusetzen wäre. Von den Eigenformen, an denen die Rahmenstiele partizipieren (1 und 4) ist die Verzweigungslast hier minimal. Für den Knicknachweis um die starke Achse mithilfe des Ersatzstabverfahrens wäre ein Knicklängenbeiwert von 2,827 zu wählen. Für die Pendelstütze (Stab 5) wäre hingegen Eigenform 2 mit einem Knicklängenbeiwert von 1,016 maßgebend. Die geringste Verzweigungslast wird hier zwar ebenfalls für Eigenform 1 berechnet, die Pendelstütze beteiligt sich an dieser Eigenform jedoch nicht (MRF = 0 %).
Um die tabellarische Analyse des MRF übersichtlicher zu gestalten, bietet es sich an, alle MRF bis zu einem gewissen Grenzwert (z. B. kleiner 20 %) über den „Ergebnistabellen-Manager“ herauszufiltern.