5216x

001635

Dipl.-Ing. (FH) Stefan Frenzel

26.05.2020

Calcul de la longueur de flambement d'un portique à deux niveaux

Les modules additionnels RF-STABILITY ou RSBUCK permettent d'effectuer des analyses de valeurs propres pour les structures filaires afin de déterminer les coefficients de longueur de flambement. Les coefficients de longueur efficace peuvent ensuite être utilisés pour l'analyse de stabilité.

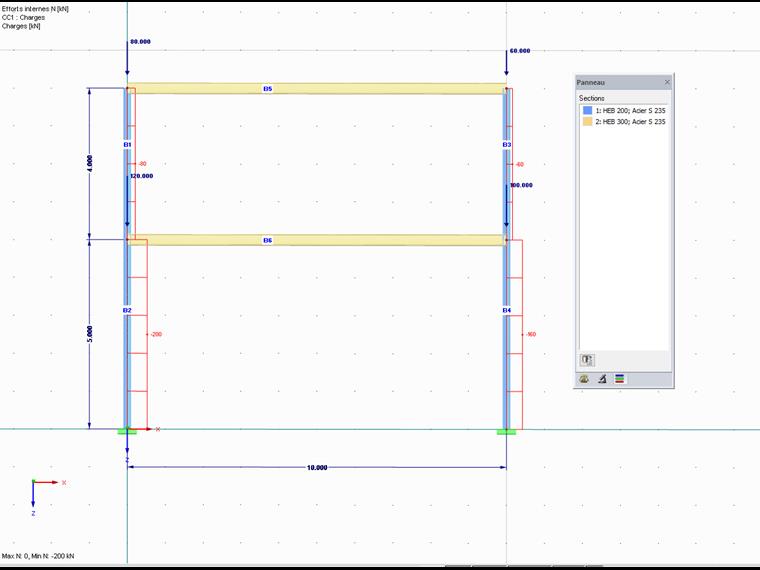
Les longueurs efficaces sont ici déterminées à l'aide d'un exemple de châssis à deux niveaux. Ces coefficients doivent être comparés avec un calcul manuel. Pour cela, un exemple tiré de la littérature spécialisée est utilisé.

Il s'agit d'une structure porteuse dont toutes les poutres doivent être de section HEB 300 et tous les poteaux de section HEB 200.

Description du modèle

Pour déterminer les longueurs efficaces, nous utilisons le tableau des longueurs efficaces du manuel allemand « Statik und Stabilität der Baukonstruktion »[1]. Les paramètres d'entrée pour utiliser les données de ce tableau sont les suivants :

y = 6 \cdot \frac{I_{Poutre}}{I_{Poteau}} \cdot \frac{l_{Poteau 1}}{l_{Poutre}} = \frac{25.170}{5.700} \cdot \frac{5, 00}{10, 00} = 13, 23; \frac{1}{y} = 0, 076 \approx 0, 1

χ = E \cdot \frac{I_{Poteau 1}}{I_{Poteau 2}} \cdot \frac{l_{2}}{l_{1}} = 1 \cdot \frac{4, 00}{5, 00} = 0, 80

κ = \frac{N_{2}}{N_{1}} \cdot \frac{l_{2}}{l_{1}} = \frac{80}{200} \cdot \frac{4, 00}{5, 00} = 0, 320

Paramètres d'entrée pour la détermination des longueurs efficaces

Lorsque la charge appliquée aux deux poteaux est la même, le tableau fournit un coefficient β' de 1,1. Cette valeur doit maintenant être convertie pour chaque poteau à l'aide des facteurs de pondération.

m = \frac{160}{200} = 0, 80

β_{1} = \sqrt{0, 5 \cdot (1 m)} \cdot β' = \sqrt{0, 5 \cdot (1 0, 80)} \cdot 1, 1 = 1, 05

β_{2} = \frac{β_{1}}{\sqrt{χ \cdot κ}} = \frac{1, 05}{\sqrt{0, 80 \cdot 0, 32}} = 2, 07

Facteurs de pondération

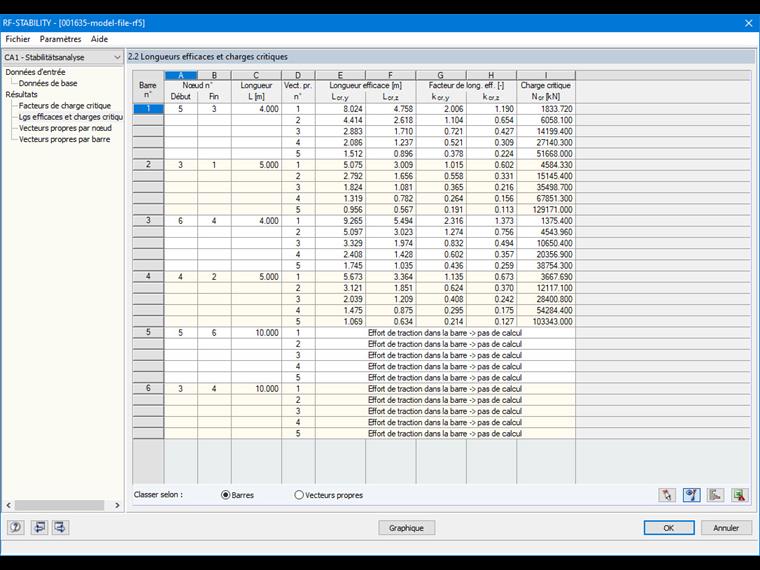
En calculant ensuite la structure avec RF-STABILITY ou RSBUCK, on obtient dans le module les coefficients de longueur efficace de chaque poteau au premier mode propre.

Sortie des résultats

Base de connaissance

Ko 001635 | Calcul de la longueur de flambement d'un portique à deux niveaux

Auteur

M. Frenzel est responsable du développement de produits pour l'analyse dynamique. Il fournit également une assistance technique aux clients de Dlubal Software.

Liens

Analyse de stabilité

Références

O résultats, P., & Richter, S. Kranbahnträger aus Walzprofilen. Vieweg & Sohn, Wiesbaden, edition = 2. 2002.
Petersen, C.: (1982). Statik und Stabilität der Baukonstruktionen , (2e édition. Wiesbaden : Vueeg.

Téléchargements

Modèle de l'article technique | Fichier RFEM 5

536 KB

;