5269x

001635

Dipl.-Ing. (FH) Stefan Frenzel

2020-05-26

Obliczanie długości efektywnych na przykładzie ramy dwukondygnacyjnej

Dzięki modułom dodatkowym RF-STABILITY lub RSBUCK dla RFEM i RSTAB, możliwe jest przeprowadzenie analizy wartości własnych dla konstrukcji prętowych w celu określenia współczynników długości efektywnej. Współczynniki te można następnie wykorzystać do obliczeń stateczności.

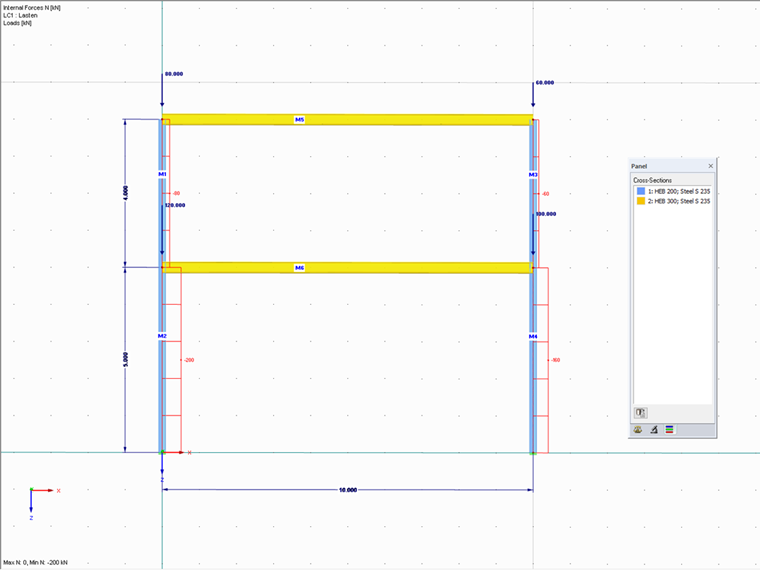
Poniższy przykład przedstawia wyznaczenie współczynników długości efektywnych dla elementów ramy dwukondygnacyjnej. Współczynniki te zostaną porównane z obliczeniami ręcznymi. W tym celu wykorzystany zostanie przykład z literatury technicznej.

Dla uproszczenia przyjęto, że analizowana konstrukcja to rama, w której wszystkie belki wykonane są z profilu HEB 300, a wszystkie słupy - z HEB 200.

Opis modelu

Aby określić długości efektywne, korzystamy z tabeli długości efektywnych z niemieckiej książki "Statik und Stabilität der Baukonstruktion"[1]. Parametry wejściowe do zastosowania tej tabeli są określone poniżej.

y = 6 \cdot \frac{I_{Riegel}}{I_{Stütze}} \cdot \frac{l_{Stütze 1}}{l_{Riegel}} = \frac{25.170}{5.700} \cdot \frac{5, 00}{10, 00} = 13, 23; \frac{1}{y} = 0, 076 \approx 0, 1

χ = E \cdot \frac{I_{Stütze 1}}{I_{Stütze 2}} \cdot \frac{l_{2}}{l_{1}} = 1 \cdot \frac{4, 00}{5, 00} = 0, 80

κ = \frac{N_{2}}{N_{1}} \cdot \frac{l_{2}}{l_{1}} = \frac{80}{200} \cdot \frac{4, 00}{5, 00} = 0, 320

Parametry wejściowe do określenia długości efektywnych

W przypadku jednakowego obciążenia obydwu słupów tabela pokazuje β '1,1. Wartość tą należy przeliczyć na poszczególne słupy za pomocą odpowiedniego współczynnika rozdziału.

m = \frac{160}{200} = 0, 80

β_{1} = \sqrt{0, 5 \cdot (1 m)} \cdot β' = \sqrt{0, 5 \cdot (1 0, 80)} \cdot 1, 1 = 1, 05

β_{2} = \frac{β_{1}}{\sqrt{χ \cdot κ}} = \frac{1, 05}{\sqrt{0, 80 \cdot 0, 32}} = 2, 07

Współczynniki ważenia

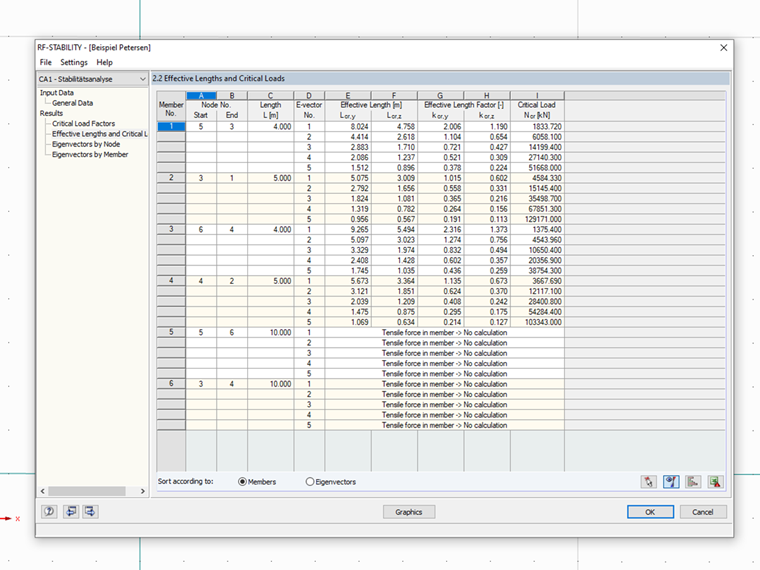
Po przeliczeniu tej konstrukcji za pomocą modułu RF-STABILITY lub RSBUCK, również otrzymywane są współczynniki długości efektywnych dla poszczególnych słupów po wskazaniu pierwszej postaci wyboczeniowej.

Wyniki

Baza informacji

KB 001635 | Obliczanie długości efektywnych na przykładzie ramy dwukondygnacyjnej

Autor

Pan Frenzel jest odpowiedzialny za rozwój produktów do analizy dynamicznej. Zajmuje się również wsparciem technicznym dla klientów Dlubal Software.

Odnośniki

Oprogramowanie Dlubal Software do analizy stateczności

Odniesienia

P. Osterrieder, S. Richter Kranbahnträger aus Walzprofilen. Vieweg & Sohn, Wiesbaden, edition = 2. 2002.
Petersen, C. (1982). Statik und Stabilität der Baukonstruktionen , red.). Wiesbaden: Widokeg.

Pobrane

Model do artykułu technicznego | Plik RFEM 5

536 KB

;