Výpočet ustáleného proudění lze vybrat v záložce "Obecné" v dialogu "Parametry simulace" (viz obrázek
Parametry simulace
).
Počáteční podmínky
Při aktivaci možnosti "Použít potenciální proudění pro výpočet počáteční podmínky" se pro vytvoření počátečních podmínek použije linearizovaná verze neviskózních Navier-Stokesových rovnic.
Výpočet ustáleného proudění
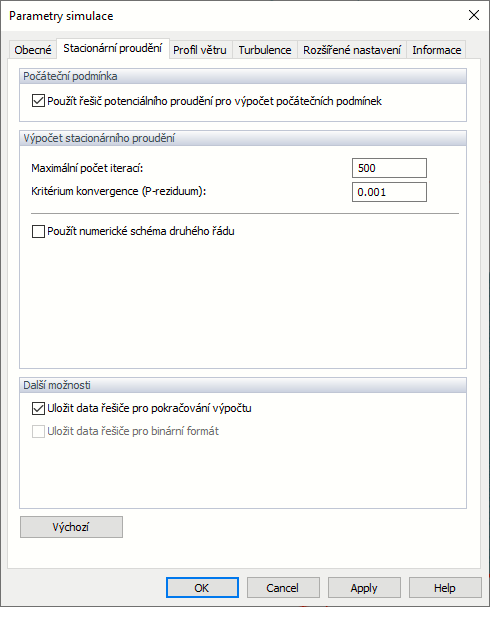
Můžete definovat "Maximální počet iterací". Ve výchozím nastavení je limit 500 iterací. Pokud výpočet konverguje v rámci menšího počtu iterací, zastaví se. Můžete také definovat "Minimální počet iterací", který je standardně nastaven na 300 iterací (viz obrázek
Možnosti programu
), bez ohledu na to, zda již bylo splněno kritérium konvergence (viz níže). Maximální počet je užitečný pro zamezení nekonečných smyček.
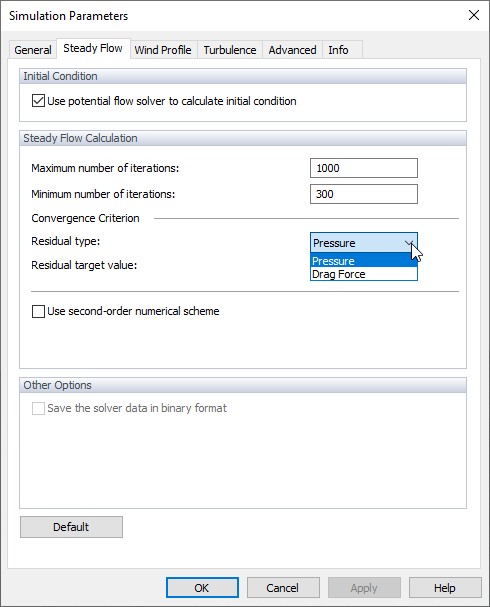
"Kritérium konvergence" představuje mez dorazu pro výpočet. K dispozici jsou dvě kritéria konvergence, lze se řídit kritériem tlaku nebo kritériem utahovací síly. Vyberte jednu z možností v poli Typ rezidua a poté nastavte cílovou hodnotu.
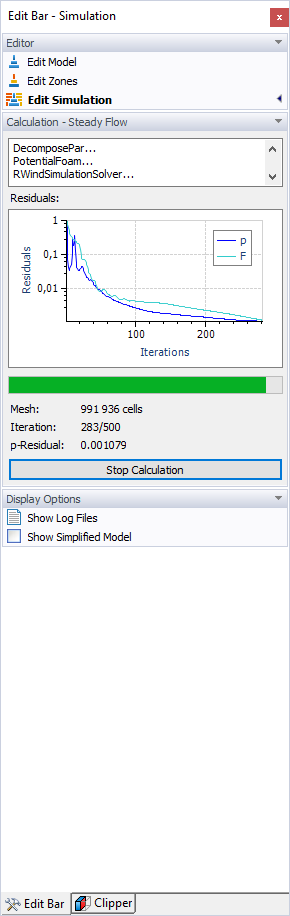
Jakmile zbytkové množství klesne pod definovanou hodnotu, výpočet se ukončí. Při výpočtu se zobrazí iterační diagram a zbytkové množství (p-zbytkové pro tlak). Je také k dispozici ve výsledcích simulace (viz kapitola Zbytky).
Zaškrtávací políčko "Použít číselné schéma druhého řádu" určuje, které číselné schéma se použije pro členy divergence (toky). Ve výchozím nastavení není aktivní, takže výpočet probíhá podle 1. řádu. Pokud je toto zaškrtávací políčko zaškrtnuté, provede se řešení druhého řádu.
Další možnosti
Ustálený řešič programu RWIND 2 plně nezachycuje "oscilační" efekty, jak je popsáno v FAQ 4731. Aby bylo možné parciální diferenciální rovnice řešit numericky, musí být všechny diferenciální členy (prostorové a časové derivace) diskretizovány. Více informací o řešičích najdete v dokumentaci Algorithms and Solvers. Existuje obrovský seznam diskretizací ("schémat"), přičemž každé schéma má určité numerické chování z hlediska přesnosti, stability a konvergence. Další informace o konvergenci najdete na CFD Direct.