RFEM et RWIND sont utilisés pour générer un modèle de structure à membrane tendue de sorte que la simulation du vent puisse être commencée, ainsi que la mise en œuvre de critères importants. RWIND est un outil puissant pour créer des charges de vent sur des structures générales et des formes complexes. Le solveur CFD est un package logiciel OpenFOAM® (version 17.10), qui donne de très bons résultats et est un outil largement utilisé pour les simulations CFD. Le solveur numérique est en régime permanent pour un écoulement turbulent incompressible, utilisant l’algorithme SIMPLE (Semi-Implicit Method for Pressure Linked Equations).
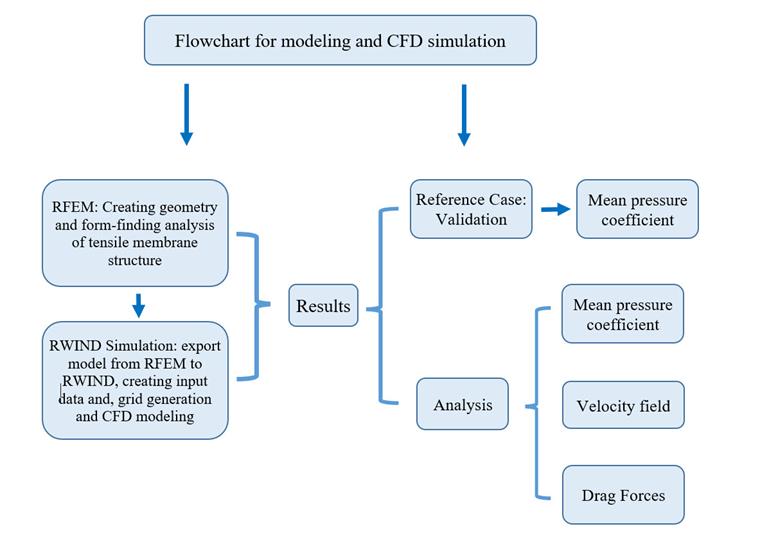
Les charges de vent sont réglementées par des normes spécifiques, telles que EN 1991-1-4, ASCE/SEI 7-16, ou NBC 2015. RFEM est un logiciel technique bien équipé pour créer des structures à membrane tendue. Il prend en compte l’analyse de recherche de forme non linéaire pour les surfaces à double courbure précontraintes. La figure 02 présente un organigramme des flux d’air numériques et une modélisation EF pour réaliser un exemple de vérification concernant les structures à membrane tendue.
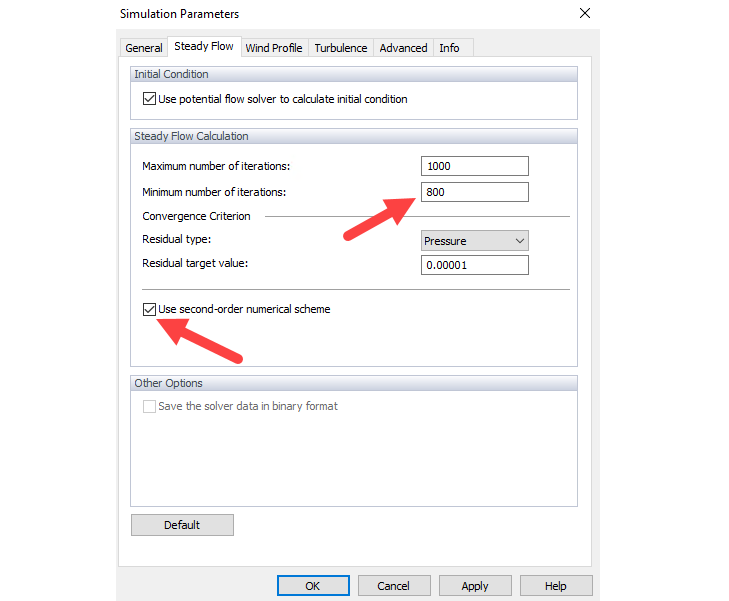
Afin de déterminer numériquement les équations aux dérivées partielles, toutes les expressions différentielles (dérivées spatiales et temporelles) doivent être discrétisées. Il existe une large gamme de méthodes de discrétisation avec différentes approches en termes de précision, de stabilité et de convergence. Généralement, l'ordre de la discrétisation illustre la précision de la simulation numérique par rapport aux solutions des équations non discrétisées d'origine. La discrétisation numérique du premier ordre génère fondamentalement une meilleure convergence que le schéma du deuxième ordre. Dans l'étude actuelle, une discrétisation du deuxième ordre est utilisée. De plus, lors de l'utilisation du schéma numérique du deuxième ordre, nous recommandons d'augmenter le nombre minimal d'itérations pour obtenir une meilleure convergence (Figure 03).
Exemple de vérification
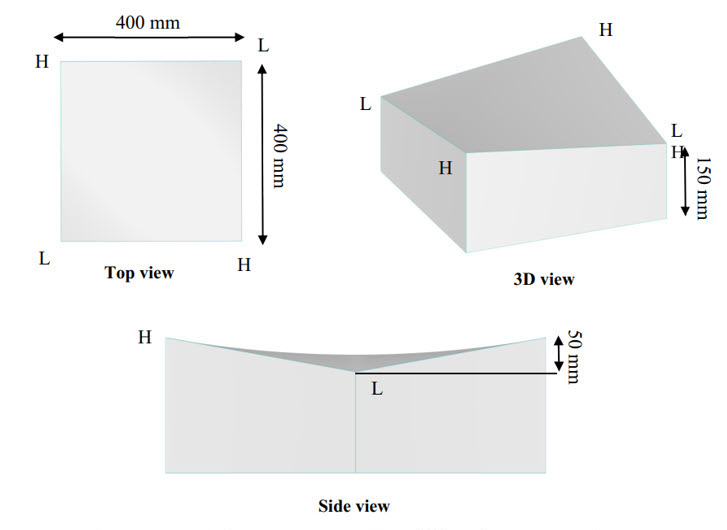
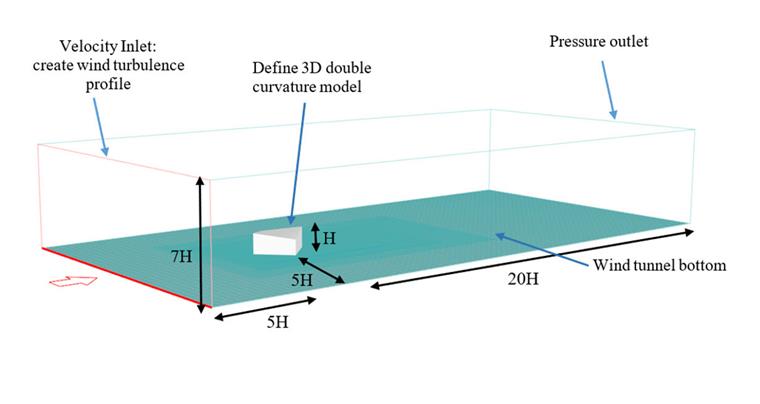
Pour vérifier le processus de simulation des flux de vent, un modèle à double courbure est développé comme le montre [1] [2], et les résultats sont analysés. L'échelle du modèle à légère courbure est sélectionnée comme 1/25, ce qui est le même que le modèle expérimental de référence [3], illustrant un toit en hyper 10 m par 10 m par 1,25 m. La légère courbure est considérée pour vérifier un exemple avec un angle θ=45o. La force de pré-tension pour l'échelle réelle a été appliquée à 2,5 kN/m sur la surface, et les propriétés mécaniques telles que le module de Young et le coefficient de Poisson sont définis comme Ex=1000 kN/m. Ey=800 kN/m. Gxy=100 kN/m, vxy=0,20. La figure 04 illustre la géométrie du modèle à double courbure. Les informations d'entrée et l'entrée de vitesse du vent pour la simulation CFD sont présentées dans la figure 05.
Dimension de la soufflerie
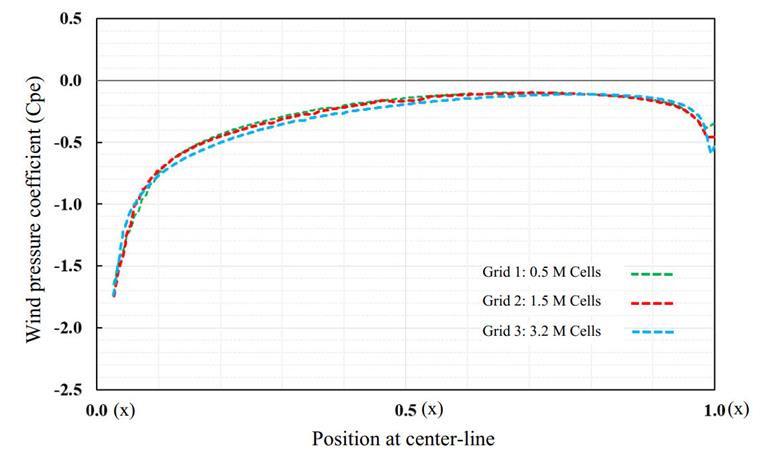
Il est important de noter que la dimension de la soufflerie peut produire des erreurs si la taille du tunnel est plus petite que le type standard. La figure suivante montre une dimension standard d'une soufflerie [3]. De plus, les résultats sont sensibles aux tailles de maillage, donc le calcul doit être effectué pour au moins trois nombres de maillage différents, et lorsque les résultats sont suffisamment proches du stade précédent, l'indépendance de la grille est atteinte (Figure 06).
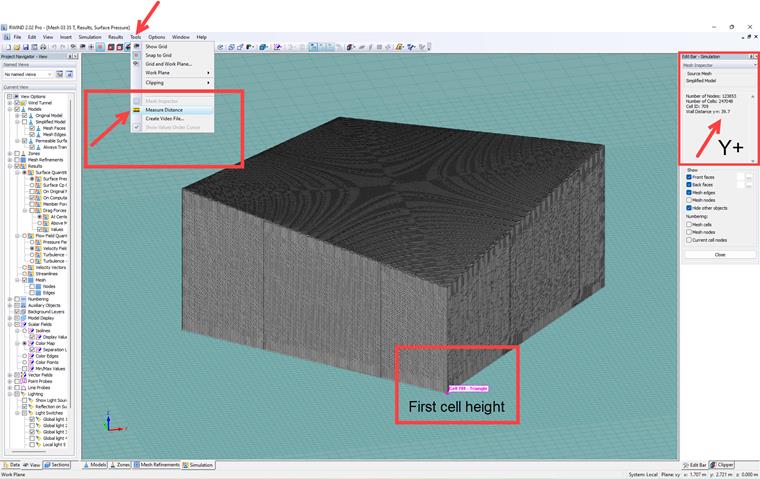
Une vue latérale de la génération de maillage du modèle est présentée dans la figure 07. Comme on peut le voir, l'algorithme de raffinement de maillage est employé à une distance proche de la surface du modèle.
Étude de la grille de calcul
Les résultats de la simulation CFD sont sensibles à la taille du maillage, donc l'indépendance de la grille doit être effectuée pour au moins trois nombres différents d'éléments de maillage. Voici les résultats de la valeur de Cp sur la ligne centrale de la toiture. Comme on peut le voir, il y a des différences très légères qui montrent que les résultats de la simulation du vent deviennent indépendants de la troisième grille (Figure 08).
Blended Wall Function
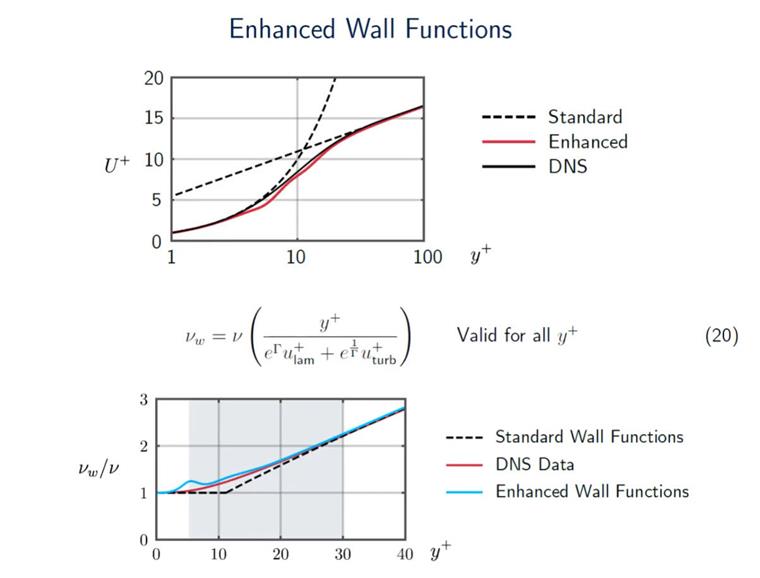
RWIND utilise la Blended Wall Function (BWF), également connue sous le nom d’Enhanced Wall Function (EWF), qui montre une bien meilleure performance que la Standard Wall Function (SWF). Ainsi, généralement, vous pouvez être sûr que vous recevrez des résultats précis pour la large gamme de nombres y+. La BWF n’est pas une fonction symétrique. Nous avons une ligne noire solide (comme le montre la figure 09), qui est la Direct Numerical Simulation (DNS) que nous essayons de reproduire. Ce que vous pouvez voir tout de suite, c'est que l'EWF est définitivement beaucoup plus proche des données DNS que le SWF. Ainsi, dans la région tampon entre un y+ de 5 et 30, l'EWF est définitivement beaucoup plus précise comparée au SWF. C’est pourquoi l’EWF est souvent recommandée dans les simulations CFD [4]. Cependant, il est important de souligner que RWIND n’est pas destiné aux investigations détaillées des couches limites impliquant de faibles valeurs de y+. RWIND est conçu comme une solution rapide, approximative, pratique, adaptée aux ingénieurs civils qui pourraient ne pas avoir une expertise étendue en CFD et qui sont intéressés à réaliser des projets industriels.
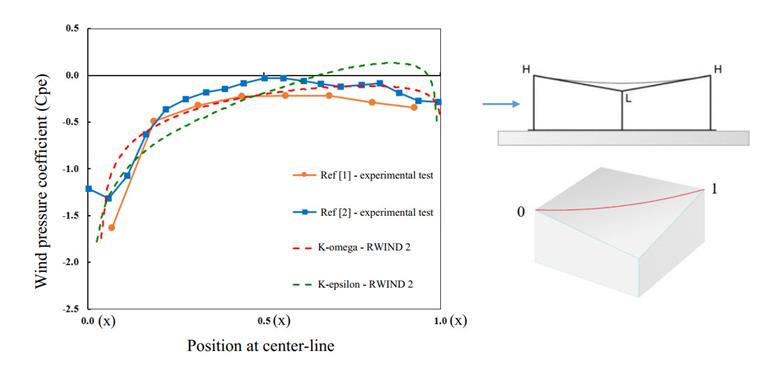
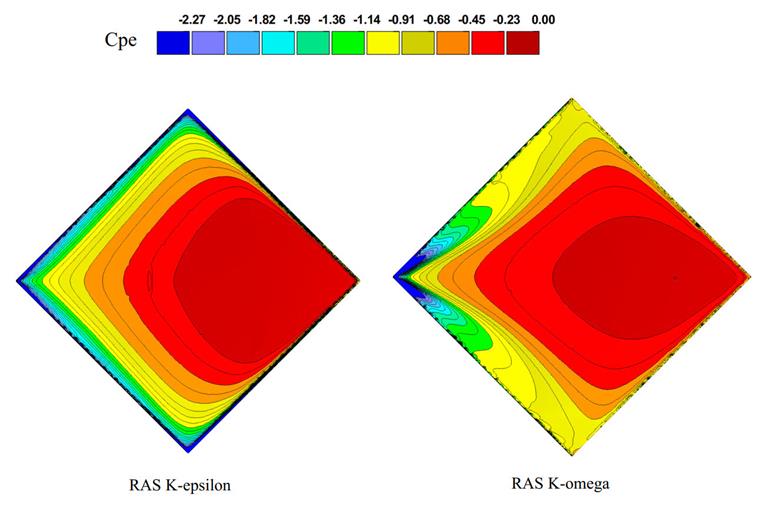
Le diagramme et le contour de pression moyenne pour les deux modèles de turbulence sont montrés dans les figures 10 et 11. Basé sur la ligne centrale du toit en hyper, le diagramme de distribution de Cpe est tracé et comparé au test expérimental en soufflerie. La valeur Cp peut être dérivée de l'équation suivante, où P est la pression du vent au point mesuré, Pref la pression de référence (pression atmosphérique), ρ est la densité de l’air, et Uref la vitesse de référence égale à 15,3 m/s.
Comme indiqué ici, le modèle de turbulence K-omega montre une meilleure performance dans la prédiction du coefficient de pression du vent. Dans l'étude actuelle, le modèle de turbulence K-omega capture les effets de détachement de vortex dans les pressions négatives élevées mieux que les modèles K-epsilon. Nous recommandons d'utiliser ce modèle de turbulence comme une option plus précise dans les interactions vent-structure.