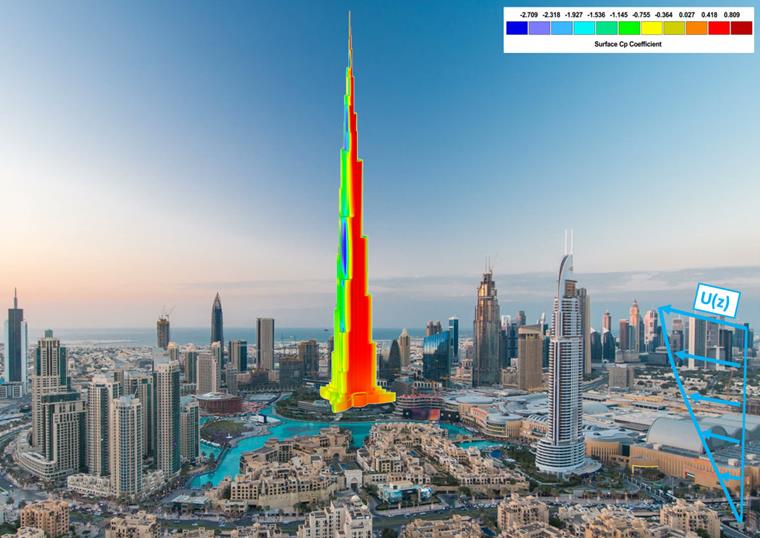
RFEM y RWIND se utilizan para generar un modelo de estructura de membrana tensada de modo que se pueda iniciar una simulación de viento, junto con la implementación de criterios importantes. RWIND es una herramienta poderosa para crear cargas de viento en estructuras generales y formas complejas. El solucionador CFD es un paquete de software OpenFOAM® (versión 17.10), que ofrece muy buenos resultados y es una herramienta ampliamente utilizada para simulaciones CFD. El solucionador numérico es en estado estacionario para flujo turbulento e incompresible, utilizando el algoritmo SIMPLE (Método Semi-Implícito para Ecuaciones Vinculadas a la Presión).
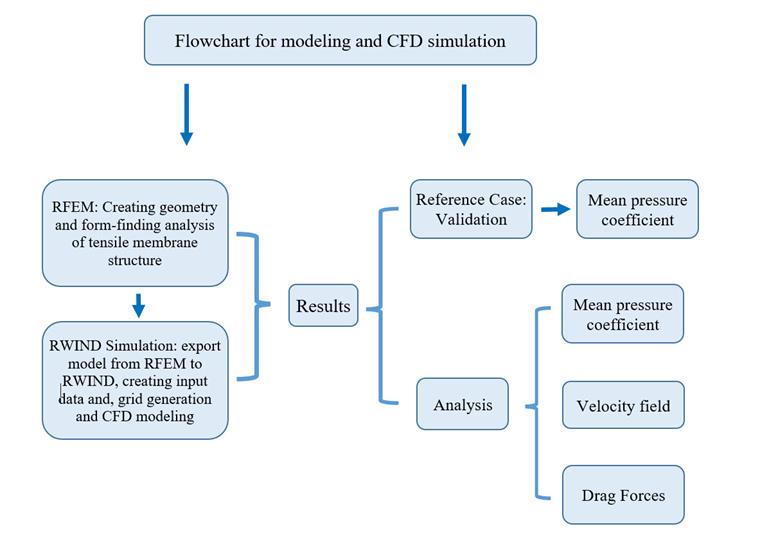
Las cargas de viento están reguladas por estándares específicos, como EN 1991-1-4, ASCE/SEI 7-16 o NBC 2015. RFEM es un software técnico bien equipado para crear estructuras de membrana tensada; considera el análisis de búsqueda de forma no lineal para superficies de doble curvatura pretensadas. La Imagen 02 presenta un diagrama de flujo de aire numérico y modelado FEM para realizar un ejemplo de verificación respecto a las estructuras de membrana tensada.
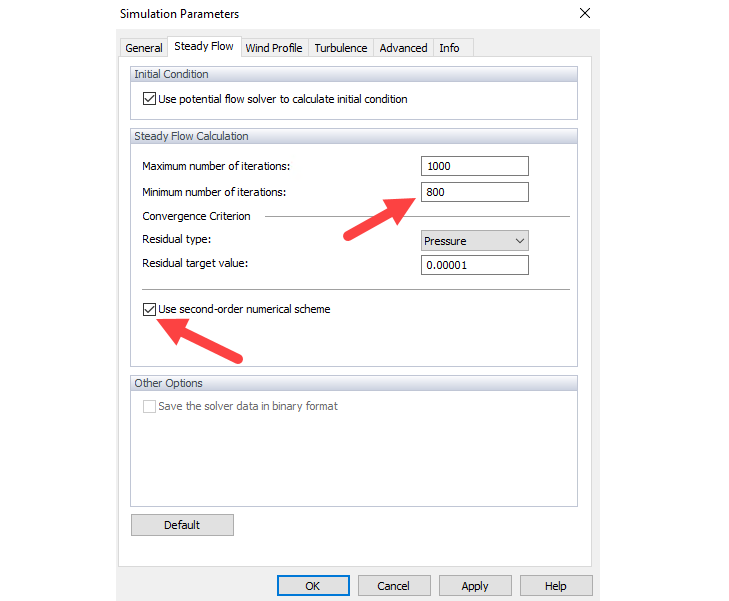
Para determinar ecuaciones diferenciales parciales numéricamente, todas las expresiones diferenciales (derivadas de espacio y tiempo) deben ser discretizadas. Existe una amplia gama de métodos de discretización con diferentes enfoques en términos de precisión, estabilidad y convergencia. Generalmente, el orden de la discretización ilustra cuán precisa es la simulación numérica en comparación con las soluciones de las ecuaciones originales no discretizadas. Básicamente, la discretización numérica de primer orden genera mejor convergencia que el esquema de segundo orden. En el estudio actual, se utiliza discretización de segundo orden. Además, al usar el esquema numérico de segundo orden, recomendamos aumentar el número mínimo de iteraciones para lograr una mejor convergencia (Imagen 03).
Ejemplo de Verificación
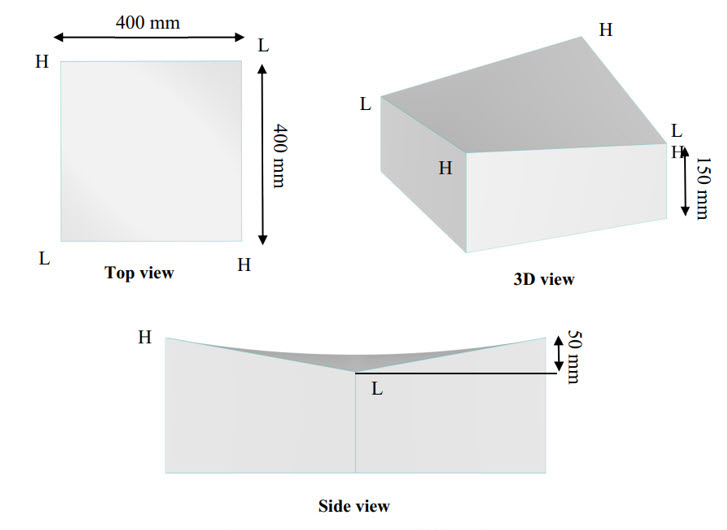
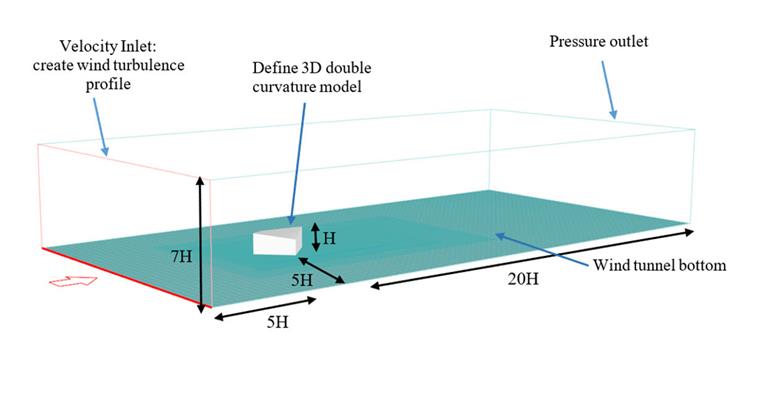
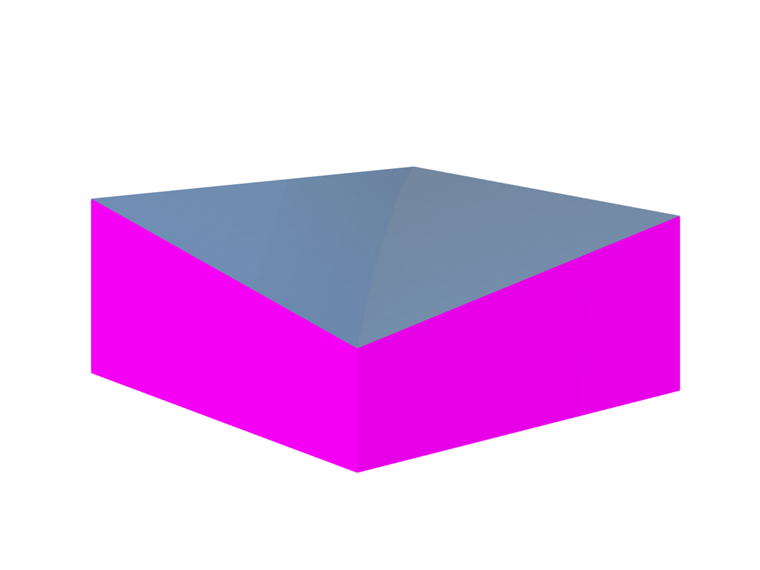
Para verificar el proceso de simulación de viento, se desarrolla un modelo de doble curvatura como se muestra en [1] [2], y se investigan los resultados. La escala del modelo de ligera curvatura se selecciona como 1/25, que es la misma que el modelo experimental en la referencia [3], ilustrando un techo hipar de 10 m por 10 m por 1.25 m. La ligera curvatura se considera para verificar un ejemplo con un ángulo θ=45o. La fuerza de pretensión para la escala real se aplicó 2.5 kN/m en la superficie, y se definen propiedades mecánicas como el módulo de Young y la relación de Poisson como Ex=1000 kN/m. Ey=800 kN/m. Gxy=100 kN/m, vxy=0.20. La Imagen 04 ilustra la geometría del modelo de doble curvatura. La información de entrada y la velocidad del viento de entrada para la simulación CFD se muestran en la Imagen 05.
Dimensión del Túnel de Viento
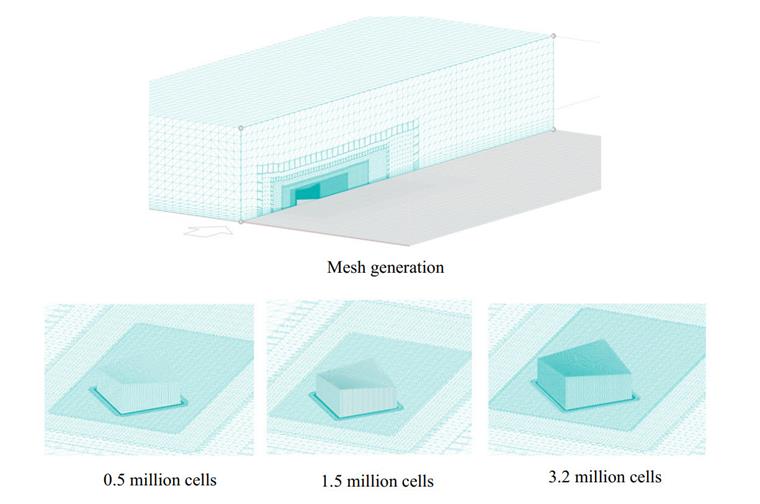
Es importante notar que la dimensión del túnel de viento puede producir errores si el tamaño del túnel es menor que el tipo estándar. La imagen siguiente muestra una dimensión estándar de un túnel de viento [3]. Además, los resultados son sensibles a los tamaños de malla, por lo que el cálculo debe realizarse para al menos tres números de malla diferentes, y cuando los resultados están lo suficientemente cerca de la etapa previa, se logra independencia de la cuadrícula (Imagen 06).
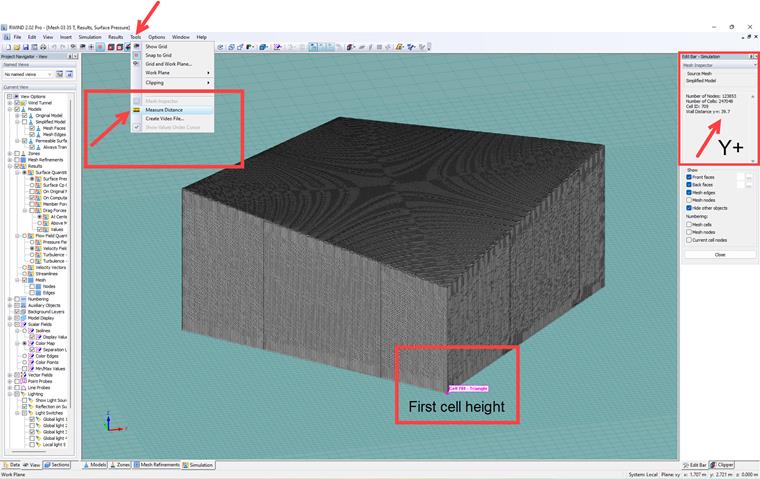
Una vista lateral de la generación de la malla del modelo se presenta en la Imagen 07; como se puede ver, se emplea el algoritmo de refinamiento de malla a una distancia cercana a la superficie del modelo.
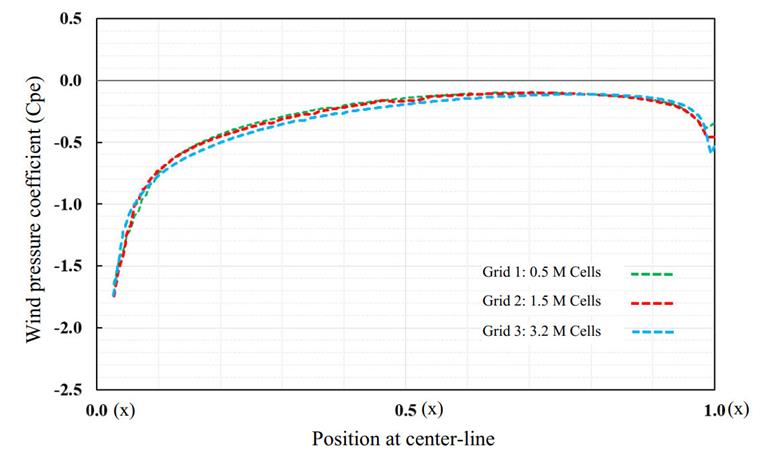
Estudio de Cuadrícula Computacional
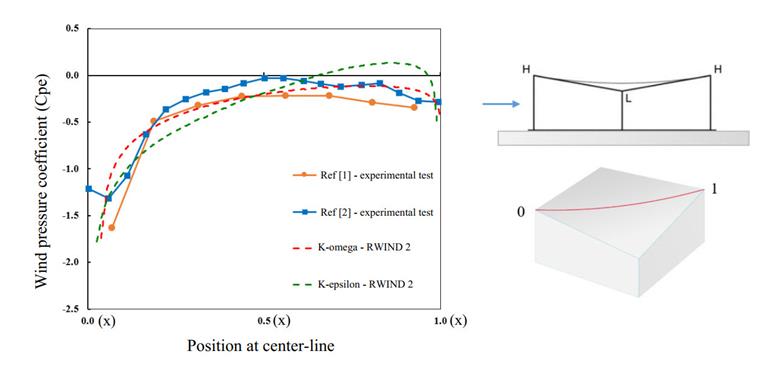
Los resultados en la simulación CFD son sensibles al tamaño de la malla, por lo que la independencia de la cuadrícula debe realizarse para al menos tres números diferentes de elementos de malla. Aquí están los resultados del valor de Cp en la línea central del techo; como se puede ver, hay diferencias muy leves que muestran que los resultados de la simulación de viento se vuelven independientes de la tercera cuadrícula (Imagen 08).
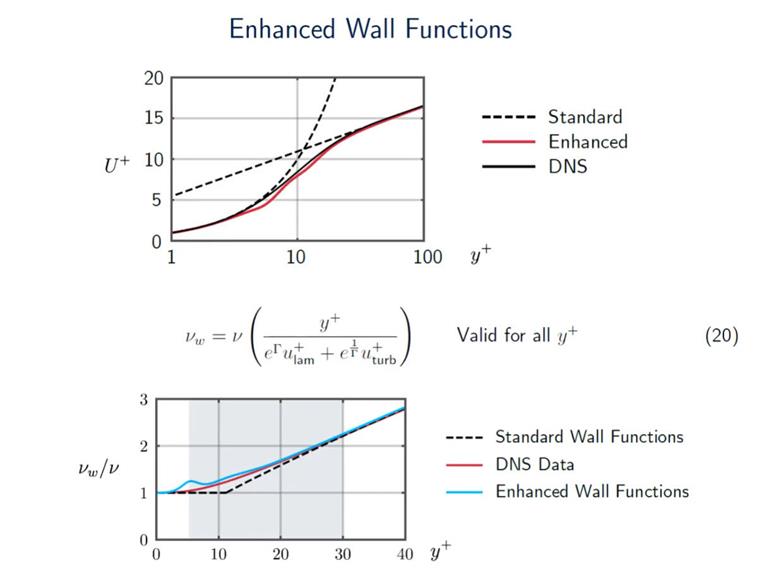
Función de Pared Mezclada
RWIND utiliza la Función de Pared Mezclada (BWF), también conocida como Función de Pared Mejorada (EWF), que muestra un rendimiento mucho mejor que la Función de Pared Estándar (SWF). Por lo tanto, generalmente puedes estar seguro de que recibirás resultados precisos para el amplio rango de números y+. La BWF no es una función simétrica. Tenemos una línea negra sólida (como se muestra en la imagen 09), que es la Simulación Numérica Directa (DNS) que estamos tratando de reproducir. Lo que puedes ver de inmediato es que la EWF está definitivamente mucho más cerca de los datos de DNS que la SWF. Por lo tanto, en la región de amortiguamiento entre un y+ de 5 y 30, la EWF es definitivamente mucho más precisa en comparación con la SWF. Esta es la razón por la cual a menudo se recomienda la EWF en simulaciones CFD [4]. Sin embargo, es importante enfatizar que RWIND no está diseñado para investigaciones detalladas de capas límite que involucren valores bajos de y+. RWIND está diseñado como una solución rápida, aproximada y práctica adaptada para ingenieros civiles que pueden no tener una experiencia extensiva en CFD y están interesados en realizar proyectos industriales.
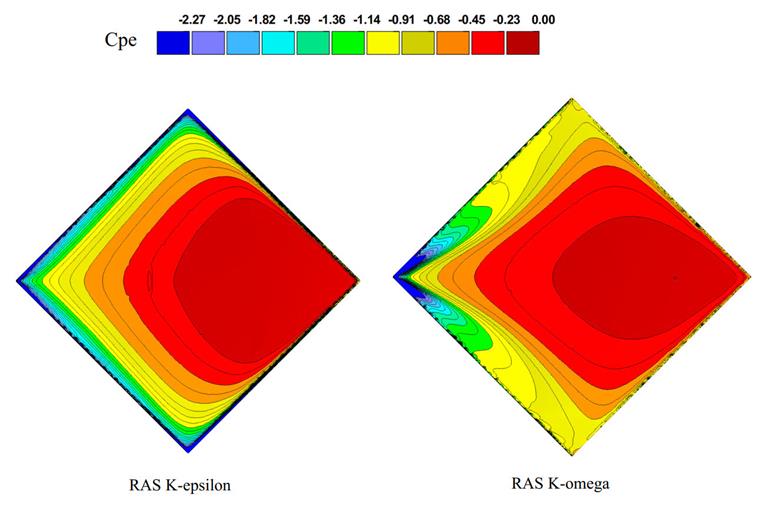
El diagrama de presión media y el contorno para los dos modelos de turbulencia se muestran en las Imágenes 10 y 11. Basado en la línea central del techo hipar, se dibuja y compara el diagrama de distribución de Cpe con la prueba experimental en túnel de viento. El valor de Cp puede derivarse de la siguiente ecuación, donde P es la presión del viento en el punto medido, Pref la presión de referencia (presión atmosférica), ρ es la densidad del aire, y Uref la velocidad de referencia igual a 15.3 m/s.
Como se muestra aquí, el modelo de turbulencia K-omega muestra un mejor rendimiento en predecir el coeficiente de presión del viento; en el estudio actual, el modelo de turbulencia K-omega captura los efectos del desprendimiento de vórtices en alta gradiente de presión negativa del viento mejor que los modelos K-epsilon. Recomendamos usar este modelo de turbulencia como una opción más precisa en interacciones viento-estructura.