Uma iteração é um processo repetitivo que se aproxima de um objetivo. Na análise estrutural numérica, este método é geralmente utilizado para encontrar uma solução para problemas com relações não lineares. Tais problemas geralmente consistem em uma equação com termos não lineares que dependem de uma variável.
O processo de iteração começa, em primeiro lugar, com a inserção de um valor inicial arbitrário para a variável desconhecida e resolve os termos do lado esquerdo e direito da equação. Se a equação não for satisfeita, o processo é repetido com um valor inicial modificado. Este procedimento iterativo é executado até que a equação seja satisfeita. Neste caso, diz-se que há convergência e o último valor utilizado para a variável é a solução.
A precisão deste procedimento depende das variáveis utilizadas. Isso significa que, para encontrar a solução exata, muitas iterações geralmente precisam ser realizadas. Se uma solução com precisão reduzida for suficiente, a convergência da iteração é vinculada a um critério de tolerância. Uma nova iteração é iniciada apenas se a diferença entre os termos do lado esquerdo e direito da equação for maior que um critério de tolerância definido.
Processos iterativos na análise estrutural
- Determinação das forças internas no sistema deformado (Teoria de Segunda Ordem)
- Simulação de propriedades de material não lineares (Plasticidade)
- Determinação de tensões de contato entre dois corpos ligados de forma conectada
Iterações no RFEM e no RSTAB
No RFEM 5 e RSTAB 8, os critérios e o número máximo de iterações para cálculos não lineares são organizados em "Cálculo" → "Parâmetros de cálculo" na aba "Parâmetros de cálculo globais".
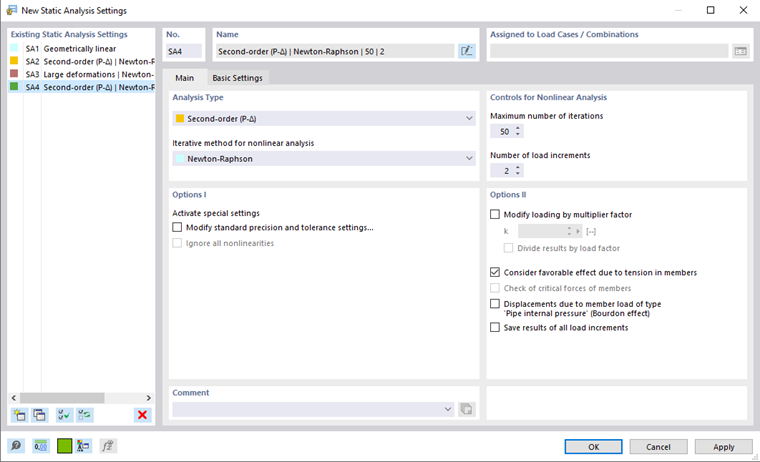
No RFEM 6 e RSTAB 9, os parâmetros para as iterações são geridos nas Configurações da Análise Estrutural.