Una iteración es un proceso repetitivo que se aproxima a un objetivo. En el análisis estructural numérico, este método se utiliza principalmente para encontrar una solución a problemas con relaciones no lineales. Tales problemas generalmente consisten en una ecuación con términos no lineales que dependen de una variable.
El proceso iterativo comienza en un primer paso insertando un valor inicial cualquiera para la variable desconocida y resolviendo los términos en el lado izquierdo y derecho de la ecuación. Si la ecuación no se cumple, el proceso se repite con un valor inicial modificado. Este proceso iterativo continúa hasta que se cumple la ecuación. En este caso, se habla de convergencia y el último valor de la variable utilizado es la solución.
La precisión de este método depende de las variables utilizadas. Esto significa que, para encontrar la solución exacta, a menudo se deben realizar muchas iteraciones. Si una solución con precisión reducida es suficiente, se asocia la convergencia de la iteración a un criterio de tolerancia. En este caso, solo se inicia una nueva iteración si la diferencia entre los términos de los lados izquierdo y derecho de la ecuación es mayor que un criterio de tolerancia definido.
Procesos iterativos en el análisis estructural
- Determinación de magnitudes de sección en el sistema deformado (Teoría del segundo orden)
- Simulación de propiedades de materiales no lineales (Plasticidad)
- Determinación de tensiones de contacto entre dos cuerpos conectados estrechamente
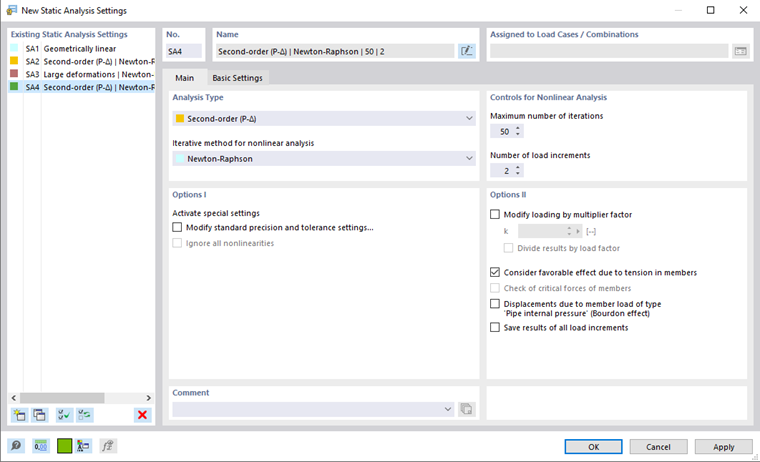
Iteraciones en RFEM y RSTAB
En RFEM 5 y RSTAB 8, los criterios y las iteraciones máximas para cálculos no lineales están organizados bajo "Cálculo" → "Parámetros de cálculo" en la pestaña "Parámetros de cálculo globales".
En RFEM 6 y RSTAB 9, los parámetros para las iteraciones se gestionan en los Configuración del análisis estático.